用于时间序列问题的特征工程

Note

This guide focuses on feature engineering for single-table time series problems; it does not cover how to handle temporal multi-table data for other machine learning problem types. A more general guide on handling time in Featuretools can be found here.

时间序列预测包括使用先前观察结果来预测目标的未来数值。在时间序列问题中使用的数据集中，数据具有固有的时间顺序（由时间索引确定），我们要预测的顺序目标值高度依赖于彼此。针对时间序列问题的特征工程利用了最近观察结果比更远观察结果更具预测性这一事实。本指南将探讨如何使用Featuretools自动化处理仅包含时间索引和目标列的单变量时间序列问题的特征工程。我们将使用一个包含一个DataFrame temperatures 的温度演示EntitySet 进行操作。temperatures 数据框包含我们将要预测的最低日温度。总共有三列：id、Temp 和 Date。id 列是Featuretools目的所必需的索引。其他两列对于单变量时间序列问题很重要：Date 是我们的时间索引，Temp 是我们的目标列。工程化的特征将从这两列构建而来。

es = load_weather()

es["temperatures"].head(10)

Downloading data ...

	id	Date	Temp
0	0	1981-01-01	20.7
1	1	1981-01-02	17.9
2	2	1981-01-03	18.8
3	3	1981-01-04	14.6
4	4	1981-01-05	15.8
5	5	1981-01-06	15.8
6	6	1981-01-07	15.8
7	7	1981-01-08	17.4
8	8	1981-01-09	21.8
9	9	1981-01-10	20.0

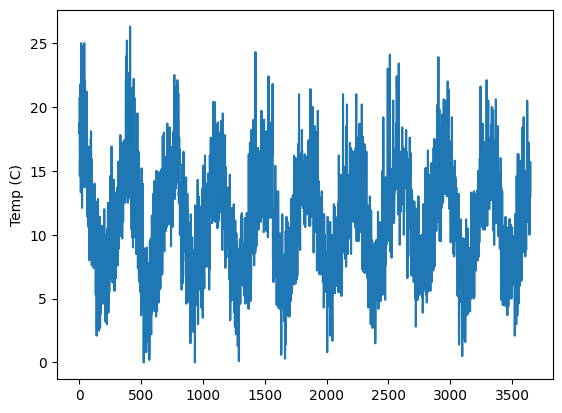
es["temperatures"]["Temp"].plot(ylabel="Temp (C)")

<Axes: ylabel='Temp (C)'>

理解特征工程窗口

在多表数据集中，目标DataFrame中单行的特征工程窗口向前延伸，覆盖子DataFrame中的观测数据，从时间索引开始，直到达到截止时间或最后时间索引为止。在单表时间序列数据集中，单个值的特征工程窗口向时间轴向后延伸。因此，截止时间和最后时间索引的概念不再以同样的方式相关。例如：对于单表时间序列数据集，截止时间将创建训练和测试数据拆分。在DFS期间，特征不会在截止时间之后计算。通常情况下，通过在创建EntitySet之前拆分数据，可以更简单地实现相同的行为，因为在特征矩阵计算时对数据进行过滤比提前拆分数据更消耗计算资源。

split_point = int(df.shape[0]*.7)
training_data = df[:split_point]
test_data = df[split_point:]

因此，由于我们无法使用现有参数来定义每个观测的特征工程窗口，我们需要定义新的概念gap和window_length。这将允许我们设置存在于每个观测之前的特征工程窗口。

Gap和Window Length

请注意，在定义gap和window_length时，我们将使用整数。这意味着我们的数据以均匀间隔发生–在本例中是每天–因此数字n对应于n天。对于不均匀间隔的支持正在进行中，可以通过Woodwork方法df.ww.infer_temporal_frequencies进行探索。如果我们处于时间点t，我们可以访问比t更早的时间的信息（过去值），而我们没有来自大于t的时间的信息（未来值）。我们在特征工程方面的限制将取决于在t之前我们确切可以访问数据的时间。考虑一个记录需要一周时间才能摄入的数据的例子；我们可以访问的最早数据是七天前的，即t - 7。我们将其称为我们的gap。gap为0将包括实例本身，我们在时间序列问题中必须小心避免这种情况，因为这会暴露我们的目标。我们还需要确定在t - 7之前我们可以回溯多久。回溯得太久，我们可能会失去最近观察的有效性，但回溯得太近，我们可能无法捕捉数据显示的全部行为谱系。在这个例子中，假设我们只想每次查看5天的数据。我们将其称为我们的window_length。

gap = 7
window_length = 5

有了这两个参数（gap和window_length）的设置，我们已经定义了我们的特征工程窗口。现在，我们可以继续定义我们的特征原语。

时间序列原语

对于时间序列问题，我们将专注于三种类型的原语。其中一种将从时间索引中提取特征，另外两种类型将从我们的目标列中提取特征。

日期时间转换原语

我们需要一种方式将时间引入到我们的时间序列特征中。是的，使用最近的温度在确定未来温度方面具有非常强的预测能力，但还有一整套历史数据表明，一年中的月份是室外温度的一个相当好的指标。然而，如果我们查看数据，我们会发现，尽管日期在变化，观测始终在同一小时进行，因此Hour原语可能不太有用。当然，在以小时为频率或更精细的频率测量的数据集中，Hour可能具有非常强的预测能力。

datetime_primitives = ["Day", "Year", "Weekday", "Month"]

完整的日期时间转换原语列表可以在这里查看。### 延迟原语我们可以对目标列进行的最简单操作是构建目标列的延迟（或滞后）版本的特征。我们将为特征工程窗口中的每个观察值创建一个特征，因此我们将在时间范围从 t - gap - window_length 到 t - gap 上进行范围。为此，我们可以使用我们的 Lag 原语，并为窗口中的每个实例创建一个原语。

delaying_primitives = [Lag(periods=i + gap) for i in range(window_length)]

滚动变换原语

由于我们可以访问整个特征工程窗口，我们可以对该窗口进行聚合。Featuretools具有几个滚动原语，我们可以使用这些原语来实现这一目的。在这里，我们将使用RollingMean和RollingMin原语，相应地设置gap和window_length。在这里，gap非常重要，因为当gap为零时，意味着当前观察的目标值存在于窗口中，这暴露了我们的目标。这个问题也存在于引用数据框中较早值的其他原语中。因此，在使用原语进行时间序列特征工程时，必须非常小心，不要在计算特征值时在目标列上使用包含当前观察的原语。

rolling_mean_primitive = RollingMean(
    window_length=window_length, gap=gap, min_periods=window_length
)

rolling_min_primitive = RollingMin(
    window_length=window_length, gap=gap, min_periods=window_length
)

滚动变换基元的完整列表可以在这里看到。## 运行DFS 现在我们已经定义了时间序列基元，我们可以将它们传递给DFS并获得我们的特征矩阵！让我们看一个实际的特征工程窗口，就像我们上面用gap和window_length定义的那样。下面是一个示例，展示了如何在不暴露目标值的情况下使用相同的特征工程窗口提取许多特征。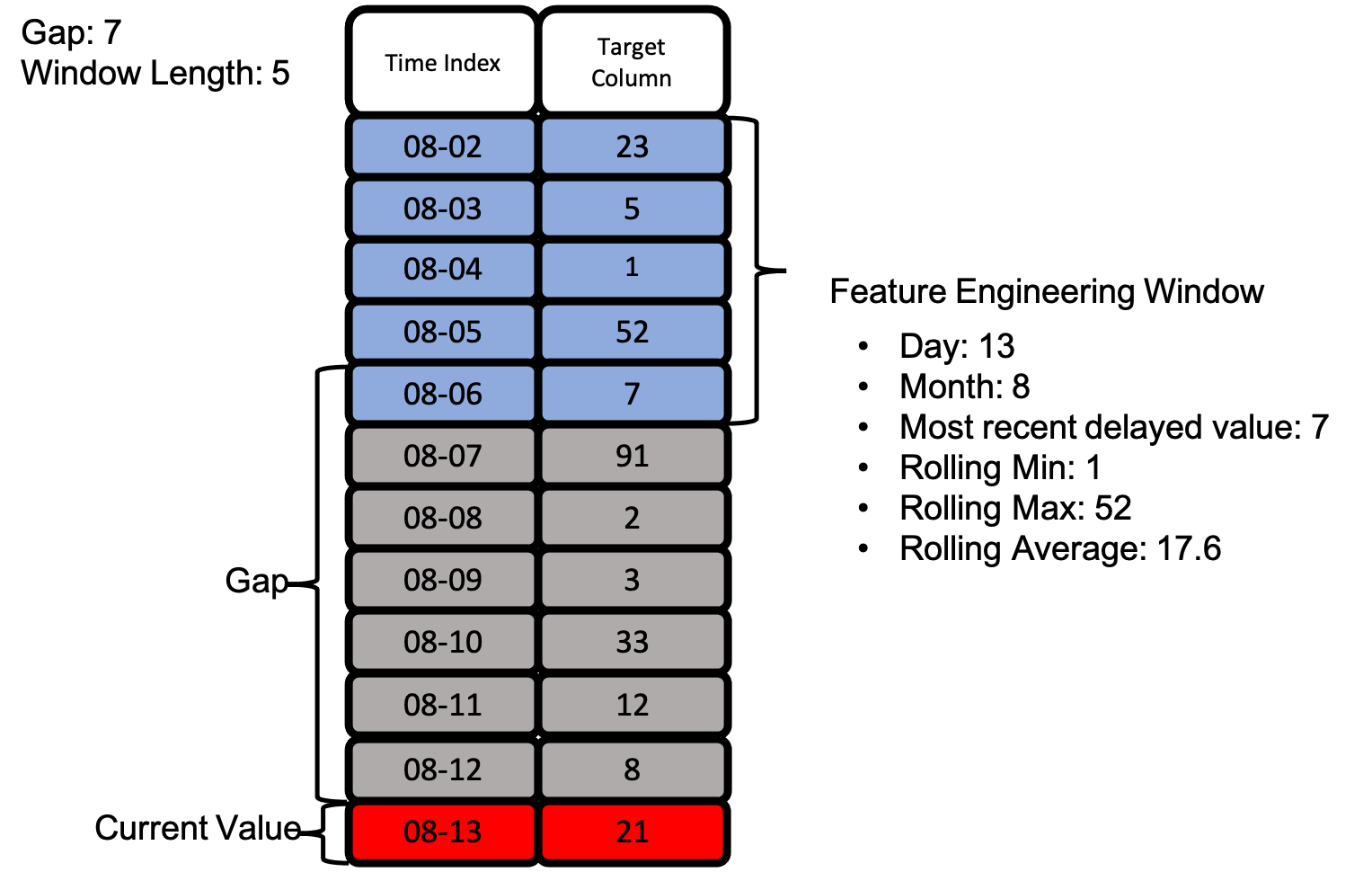通过上面的图片，我们可以看到如何使用所有定义的基元来从我们只能访问两列的情况下创建许多特征。

fm, f = ft.dfs(
    entityset=es,
    target_dataframe_name="temperatures",
    trans_primitives=(
        datetime_primitives
        + delaying_primitives
        + [rolling_mean_primitive, rolling_min_primitive]
    ),
    cutoff_time=pd.Timestamp("1987-1-30"),
)

f

[<Feature: Temp>,
 <Feature: DAY(Date)>,
 <Feature: LAG(Temp, Date, periods=10)>,
 <Feature: LAG(Temp, Date, periods=11)>,
 <Feature: LAG(Temp, Date, periods=7)>,
 <Feature: LAG(Temp, Date, periods=8)>,
 <Feature: LAG(Temp, Date, periods=9)>,
 <Feature: MONTH(Date)>,
 <Feature: ROLLING_MEAN(Date, Temp, window_length=5, gap=7, min_periods=5)>,
 <Feature: ROLLING_MIN(Date, Temp, window_length=5, gap=7, min_periods=5)>,
 <Feature: WEEKDAY(Date)>,
 <Feature: YEAR(Date)>]

fm.iloc[:, [0, 2, 6, 7, 8, 9]].head(15)

	Temp	LAG(Temp, Date, periods=10)	LAG(Temp, Date, periods=9)	MONTH(Date)	ROLLING_MEAN(Date, Temp, window_length=5, gap=7, min_periods=5)	ROLLING_MIN(Date, Temp, window_length=5, gap=7, min_periods=5)
id
0	20.7	NaN	NaN	1	NaN	NaN
1	17.9	NaN	NaN	1	NaN	NaN
2	18.8	NaN	NaN	1	NaN	NaN
3	14.6	NaN	NaN	1	NaN	NaN
4	15.8	NaN	NaN	1	NaN	NaN
5	15.8	NaN	NaN	1	NaN	NaN
6	15.8	NaN	NaN	1	NaN	NaN
7	17.4	NaN	NaN	1	NaN	NaN
8	21.8	NaN	NaN	1	NaN	NaN
9	20.0	NaN	20.7	1	NaN	NaN
10	16.2	20.7	17.9	1	NaN	NaN
11	13.3	17.9	18.8	1	17.56	14.6
12	16.7	18.8	14.6	1	16.58	14.6
13	21.5	14.6	15.8	1	16.16	14.6
14	25.0	15.8	15.8	1	15.88	14.6

上面是我们的时间序列特征矩阵！滚动和延迟特征是从我们的目标列构建的，但不会暴露它。现在我们可以使用特征矩阵来创建一个机器学习模型，用于预测未来的最低日温度。