药物分子生成与VAE
作者: Victor Basu
创建日期: 2022/03/10
最后修改: 2022/03/24
描述: 实现用于药物发现的卷积变分自编码器(VAE)。
介绍
在这个例子中,我们使用变分自编码器生成用于药物发现的分子。 我们使用研究论文 使用基于数据驱动的连续分子表示进行自动化化学设计 和 MolGAN:小分子图的隐式生成模型 作为参考。
论文使用基于数据驱动的连续分子表示进行自动化化学设计中描述的模型通过有效探索化合物的开放空间生成新分子。该模型由三个组成部分构成:编码器、解码器和预测器。编码器将分子的离散表示转换为实值连续向量,解码器将这些连续向量转换回离散分子表示。预测器从分子的潜在连续向量表示中估计化学性质。连续表示允许使用基于梯度的优化,从而有效地指导对优化功能化合物的搜索。
图(a) - 用于分子设计的自编码器的示意图,包括联合属性预测模型。从离散的分子表示(例如,SMILES字符串)开始,编码器网络将每个分子转换为潜在空间中的向量,这实质上是连续的分子表示。给定潜在空间中的一个点,解码器网络生成相应的SMILES字符串。多层感知机网络估计与每个分子相关的目标属性值。
图(b) - 在连续潜在空间中的基于梯度的优化。在对f(z)进行训练以预测基于其潜在表示z的分子性质后,我们可以针对z优化f(z)以找到预计满足特定期望属性的新潜在表示。这些新的潜在表示随后可以解码为SMILES字符串,此时可以对其性质进行实证测试。
有关MolGAN的解释和实现,请参考Keras示例 使用R-GCN生成小分子图的WGAN-GP由 Alexander Kensert提供。本示例中使用的许多功能来自上述Keras示例。
设置
RDKit是一个开源的化学信息学和机器学习工具包。如果您对药物发现领域感兴趣,该工具包将非常适用。在本示例中,RDKit用于方便高效地将SMILES转换为分子对象,然后从中获取原子和键的集合。
“SMILES以ASCII字符串的形式表达给定分子的结构。SMILES字符串是一种紧凑编码,对于较小的分子来说,相对易于人类阅读。将分子编码为字符串既缓解又促进了对给定分子的数据库和/或网络搜索。RDKit使用算法将给定的SMILES准确转换为分子对象,然后可以用来计算大量的分子性质/特征。”
!pip -q install rdkit-pypi==2021.9.4
import ast
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
from rdkit import Chem, RDLogger
from rdkit.Chem import BondType
from rdkit.Chem.Draw import MolsToGridImage
RDLogger.DisableLog("rdApp.*")
[K |████████████████████████████████| 20.6 MB 1.2 MB/s
[?25h
数据集
我们使用ZINC – 一个用于虚拟筛选的可商业获取化合物的免费数据库数据集。该数据集包含以SMILES表示的分子公式以及其各自的分子性质,如logP(水-辛醇分配系数)、SAS(合成可达性评分)和QED(药物相似性的定性估计)。
csv_path = keras.utils.get_file(
"/content/250k_rndm_zinc_drugs_clean_3.csv",
"https://raw.githubusercontent.com/aspuru-guzik-group/chemical_vae/master/models/zinc_properties/250k_rndm_zinc_drugs_clean_3.csv",
)
df = pd.read_csv("/content/250k_rndm_zinc_drugs_clean_3.csv")
df["smiles"] = df["smiles"].apply(lambda s: s.replace("\n", ""))
df.head()
从 https://raw.githubusercontent.com/aspuru-guzik-group/chemical_vae/master/models/zinc_properties/250k_rndm_zinc_drugs_clean_3.csv 下载数据
22606589/22606589 [==============================] - 0s 0us/step
| smiles | logP | qed | SAS | |
|---|---|---|---|---|
| 0 | CC(C)(C)c1ccc2occ(CC(=O)Nc3ccccc3F)c2c1 | 5.05060 | 0.702012 | 2.084095 |
| 1 | C[C@@H]1CC(Nc2cncc(-c3nncn3C)c2)C[C@@H](C)C1 | 3.11370 | 0.928975 | 3.432004 |
| 2 | N#Cc1ccc(-c2ccc(O[C@@H](C(=O)N3CCCC3)c3ccccc3)... | 4.96778 | 0.599682 | 2.470633 |
| 3 | CCOC(=O)[C@@H]1CCCN(C(=O)c2nc(-c3ccc(C)cc3)n3c... | 4.00022 | 0.690944 | 2.822753 |
| 4 | N#CC1=C(SCC(=O)Nc2cccc(Cl)c2)N=C([O-])[C@H](C#... | 3.60956 | 0.789027 | 4.035182 |
超参数
SMILE_CHARSET = '["C", "B", "F", "I", "H", "O", "N", "S", "P", "Cl", "Br"]'
bond_mapping = {"SINGLE": 0, "DOUBLE": 1, "TRIPLE": 2, "AROMATIC": 3}
bond_mapping.update(
{0: BondType.SINGLE, 1: BondType.DOUBLE, 2: BondType.TRIPLE, 3: BondType.AROMATIC}
)
SMILE_CHARSET = ast.literal_eval(SMILE_CHARSET)
MAX_MOLSIZE = max(df["smiles"].str.len())
SMILE_to_index = dict((c, i) for i, c in enumerate(SMILE_CHARSET))
index_to_SMILE = dict((i, c) for i, c in enumerate(SMILE_CHARSET))
atom_mapping = dict(SMILE_to_index)
atom_mapping.update(index_to_SMILE)
BATCH_SIZE = 100
EPOCHS = 10
VAE_LR = 5e-4
NUM_ATOMS = 120 # 最大原子数量
ATOM_DIM = len(SMILE_CHARSET) # 原子类型数量
BOND_DIM = 4 + 1 # 键类型数量
LATENT_DIM = 435 # 潜在空间大小
def smiles_to_graph(smiles):
# 将 SMILES 转换为分子对象
molecule = Chem.MolFromSmiles(smiles)
# 初始化邻接和特性张量
adjacency = np.zeros((BOND_DIM, NUM_ATOMS, NUM_ATOMS), "float32")
features = np.zeros((NUM_ATOMS, ATOM_DIM), "float32")
# 循环遍历分子中的每个原子
for atom in molecule.GetAtoms():
i = atom.GetIdx()
atom_type = atom_mapping[atom.GetSymbol()]
features[i] = np.eye(ATOM_DIM)[atom_type]
# 循环遍历一跳邻居
for neighbor in atom.GetNeighbors():
j = neighbor.GetIdx()
bond = molecule.GetBondBetweenAtoms(i, j)
bond_type_idx = bond_mapping[bond.GetBondType().name]
adjacency[bond_type_idx, [i, j], [j, i]] = 1
# 无键连接时,在最后一个通道中添加 1(表示“非键”)
# 注意:频道优先
adjacency[-1, np.sum(adjacency, axis=0) == 0] = 1
# 无原子时,在最后一列中添加 1(表示“非原子”)
features[np.where(np.sum(features, axis=1) == 0)[0], -1] = 1
return adjacency, features
def graph_to_molecule(graph):
# 解包图
adjacency, features = graph
# RWMol 是一个旨在进行编辑的分子对象
molecule = Chem.RWMol()
# 移除“无原子” & 无键的原子
keep_idx = np.where(
(np.argmax(features, axis=1) != ATOM_DIM - 1)
& (np.sum(adjacency[:-1], axis=(0, 1)) != 0)
)[0]
features = features[keep_idx]
adjacency = adjacency[:, keep_idx, :][:, :, keep_idx]
# 将原子添加到分子中
for atom_type_idx in np.argmax(features, axis=1):
atom = Chem.Atom(atom_mapping[atom_type_idx])
_ = molecule.AddAtom(atom)
# 在分子中的原子之间添加键;基于 [对称] 邻接张量的上三角
(bonds_ij, atoms_i, atoms_j) = np.where(np.triu(adjacency) == 1)
for (bond_ij, atom_i, atom_j) in zip(bonds_ij, atoms_i, atoms_j):
if atom_i == atom_j or bond_ij == BOND_DIM - 1:
continue
bond_type = bond_mapping[bond_ij]
molecule.AddBond(int(atom_i), int(atom_j), bond_type)
# 消毒分子;有关消毒的更多信息,请参见
# https://www.rdkit.org/docs/RDKit_Book.html#molecular-sanitization
flag = Chem.SanitizeMol(molecule, catchErrors=True)
# 我们要严格。如果消毒失败,返回 None
if flag != Chem.SanitizeFlags.SANITIZE_NONE:
return None
return molecule
生成训练集
train_df = df.sample(frac=0.75, random_state=42) # 随机状态是种子值 train_df.reset_index(drop=True, inplace=True)
adjacency_tensor, feature_tensor, qed_tensor = [], [], [] for idx in range(8000): adjacency, features = smiles_to_graph(train_df.loc[idx]["smiles"]) qed = train_df.loc[idx]["qed"] adjacency_tensor.append(adjacency) feature_tensor.append(features) qed_tensor.append(qed)
adjacency_tensor = np.array(adjacency_tensor) feature_tensor = np.array(feature_tensor) qed_tensor = np.array(qed_tensor)
class RelationalGraphConvLayer(keras.layers.Layer): def init( self, units=128, activation="relu", use_bias=False, kernel_initializer="glorot_uniform", bias_initializer="zeros", kernel_regularizer=None, bias_regularizer=None, kwargs ): super().init(kwargs)
self.units = units
self.activation = keras.activations.get(activation)
self.use_bias = use_bias
self.kernel_initializer = keras.initializers.get(kernel_initializer)
self.bias_initializer = keras.initializers.get(bias_initializer)
self.kernel_regularizer = keras.regularizers.get(kernel_regularizer)
self.bias_regularizer = keras.regularizers.get(bias_regularizer)
def build(self, input_shape):
bond_dim = input_shape[0][1]
atom_dim = input_shape[1][2]
self.kernel = self.add_weight(
shape=(bond_dim, atom_dim, self.units),
initializer=self.kernel_initializer,
regularizer=self.kernel_regularizer,
trainable=True,
name="W",
dtype=tf.float32,
)
if self.use_bias:
self.bias = self.add_weight(
shape=(bond_dim, 1, self.units),
initializer=self.bias_initializer,
regularizer=self.bias_regularizer,
trainable=True,
name="b",
dtype=tf.float32,
)
self.built = True
def call(self, inputs, training=False):
adjacency, features = inputs
# 从邻居聚合信息
x = tf.matmul(adjacency, features[:, None, :, :])
# 应用线性变换
x = tf.matmul(x, self.kernel)
if self.use_bias:
x += self.bias
# 减少键类型维度
x_reduced = tf.reduce_sum(x, axis=1)
# 应用非线性变换
return self.activation(x_reduced)
---
## 构建编码器和解码器
编码器以分子的图邻接矩阵和特征矩阵作为输入。这些特征通过图卷积层进行处理,然后被展平并通过多个密集层处理,以得出 `z_mean` 和 `log_var`,即分子的潜在空间表示。
**图卷积层**:关系图卷积层实现非线性变换的邻域聚合。我们可以将这些层定义如下:
`H_hat**(l+1) = σ(D_hat**(-1) * A_hat * H_hat**(l+1) * W**(l))`
其中 `σ` 表示非线性变换(通常为 ReLU 激活),`A` 为邻接张量,`H_hat**(l)` 为第 `l` 层的特征张量,`D_hat**(-1)` 为 `A_hat` 的逆对角度数张量,`W_hat**(l)` 为第 `l` 层的可训练权重张量。具体来说,对于每种键类型(关系),度数张量在对角线上表示与每个原子相连的键的数量。
来源:
[WGAN-GP与R-GCN用于生成小分子图](https://keras.io/examples/generative/wgan-graphs/)
解码器以潜在空间表示为输入,并预测相应分子的图邻接矩阵和特征矩阵。
```python
def get_encoder(
gconv_units, latent_dim, adjacency_shape, feature_shape, dense_units, dropout_rate
):
adjacency = keras.layers.Input(shape=adjacency_shape)
features = keras.layers.Input(shape=feature_shape)
# 通过一个或多个图卷积层传播
features_transformed = features
for units in gconv_units:
features_transformed = RelationalGraphConvLayer(units)(
[adjacency, features_transformed]
)
# 将分子的2-D表示降低为1-D
x = keras.layers.GlobalAveragePooling1D()(features_transformed)
# 通过一个或多个密集连接层传播
for units in dense_units:
x = layers.Dense(units, activation="relu")(x)
x = layers.Dropout(dropout_rate)(x)
z_mean = layers.Dense(latent_dim, dtype="float32", name="z_mean")(x)
log_var = layers.Dense(latent_dim, dtype="float32", name="log_var")(x)
encoder = keras.Model([adjacency, features], [z_mean, log_var], name="encoder")
return encoder
def get_decoder(dense_units, dropout_rate, latent_dim, adjacency_shape, feature_shape):
latent_inputs = keras.Input(shape=(latent_dim,))
x = latent_inputs
for units in dense_units:
x = keras.layers.Dense(units, activation="tanh")(x)
x = keras.layers.Dropout(dropout_rate)(x)
# 将前一层的输出(x)映射到[连续]邻接张量(x_adjacency)
x_adjacency = keras.layers.Dense(tf.math.reduce_prod(adjacency_shape))(x)
x_adjacency = keras.layers.Reshape(adjacency_shape)(x_adjacency)
# 在最后两个维度上将张量对称化
x_adjacency = (x_adjacency + tf.transpose(x_adjacency, (0, 1, 3, 2))) / 2
x_adjacency = keras.layers.Softmax(axis=1)(x_adjacency)
# 将前一层的输出(x)映射到[连续]特征张量(x_features)
x_features = keras.layers.Dense(tf.math.reduce_prod(feature_shape))(x)
x_features = keras.layers.Reshape(feature_shape)(x_features)
x_features = keras.layers.Softmax(axis=2)(x_features)
decoder = keras.Model(
latent_inputs, outputs=[x_adjacency, x_features], name="decoder"
)
return decoder
构建采样层
class Sampling(layers.Layer):
def call(self, inputs):
z_mean, z_log_var = inputs
batch = tf.shape(z_log_var)[0]
dim = tf.shape(z_log_var)[1]
epsilon = tf.keras.backend.random_normal(shape=(batch, dim))
return z_mean + tf.exp(0.5 * z_log_var) * epsilon
构建变分自编码器(VAE)
该模型旨在优化四个损失:
- 分类交叉熵
- KL 散度损失
- 属性预测损失
- 图损失(梯度惩罚)
分类交叉熵损失函数衡量模型的重建准确性。属性预测损失估计在经过属性预测模型运行潜在表示后,预测与实际属性之间的均方误差。模型的属性预测通过二元交叉熵进行优化。梯度惩罚进一步受到模型属性(QED)预测的指导。
梯度惩罚是对 1-Lipschitz 连续性的另一种软约束,作为对原始神经网络的梯度裁剪方案的改进(“1-Lipschitz 连续性”意味着在函数的每个点上梯度的范数最多为 1)。它为损失函数添加了一个正则化项。
class MoleculeGenerator(keras.Model):
def __init__(self, encoder, decoder, max_len, **kwargs):
super().__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
self.property_prediction_layer = layers.Dense(1)
self.max_len = max_len
self.train_total_loss_tracker = keras.metrics.Mean(name="train_total_loss")
self.val_total_loss_tracker = keras.metrics.Mean(name="val_total_loss")
def train_step(self, data):
adjacency_tensor, feature_tensor, qed_tensor = data[0]
graph_real = [adjacency_tensor, feature_tensor]
self.batch_size = tf.shape(qed_tensor)[0]
with tf.GradientTape() as tape:
z_mean, z_log_var, qed_pred, gen_adjacency, gen_features = self(
graph_real, training=True
)
graph_generated = [gen_adjacency, gen_features]
total_loss = self._compute_loss(
z_log_var, z_mean, qed_tensor, qed_pred, graph_real, graph_generated
)
grads = tape.gradient(total_loss, self.trainable_weights)
self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
self.train_total_loss_tracker.update_state(total_loss)
return {"loss": self.train_total_loss_tracker.result()}
def _compute_loss(
self, z_log_var, z_mean, qed_true, qed_pred, graph_real, graph_generated
):
adjacency_real, features_real = graph_real
adjacency_gen, features_gen = graph_generated
adjacency_loss = tf.reduce_mean(
tf.reduce_sum(
keras.losses.categorical_crossentropy(adjacency_real, adjacency_gen),
axis=(1, 2),
)
)
features_loss = tf.reduce_mean(
tf.reduce_sum(
keras.losses.categorical_crossentropy(features_real, features_gen),
axis=(1),
)
)
kl_loss = -0.5 * tf.reduce_sum(
1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var), 1
)
kl_loss = tf.reduce_mean(kl_loss)
property_loss = tf.reduce_mean(
keras.losses.binary_crossentropy(qed_true, qed_pred)
)
graph_loss = self._gradient_penalty(graph_real, graph_generated)
return kl_loss + property_loss + graph_loss + adjacency_loss + features_loss
def _gradient_penalty(self, graph_real, graph_generated):
# 解压图形
adjacency_real, features_real = graph_real
adjacency_generated, features_generated = graph_generated
# 生成插值图(adjacency_interp 和 features_interp)
alpha = tf.random.uniform([self.batch_size])
alpha = tf.reshape(alpha, (self.batch_size, 1, 1, 1))
adjacency_interp = (adjacency_real * alpha) + (1 - alpha) * adjacency_generated
alpha = tf.reshape(alpha, (self.batch_size, 1, 1))
features_interp = (features_real * alpha) + (1 - alpha) * features_generated
# 计算插值图的 logits
with tf.GradientTape() as tape:
tape.watch(adjacency_interp)
tape.watch(features_interp)
_, _, logits, _, _ = self(
[adjacency_interp, features_interp], training=True
)
# 计算相对于插值图的梯度
grads = tape.gradient(logits, [adjacency_interp, features_interp])
# 计算梯度惩罚
grads_adjacency_penalty = (1 - tf.norm(grads[0], axis=1)) ** 2
grads_features_penalty = (1 - tf.norm(grads[1], axis=2)) ** 2
return tf.reduce_mean(
tf.reduce_mean(grads_adjacency_penalty, axis=(-2, -1))
+ tf.reduce_mean(grads_features_penalty, axis=(-1))
)
def inference(self, batch_size):
z = tf.random.normal((batch_size, LATENT_DIM))
reconstruction_adjacency, reconstruction_features = model.decoder.predict(z)
# 获取单热编码的邻接张量
adjacency = tf.argmax(reconstruction_adjacency, axis=1)
adjacency = tf.one_hot(adjacency, depth=BOND_DIM, axis=1)
# 从邻接矩阵中移除潜在的自环
adjacency = tf.linalg.set_diag(adjacency, tf.zeros(tf.shape(adjacency)[:-1]))
# 获取单热编码的特征张量
features = tf.argmax(reconstruction_features, axis=2)
features = tf.one_hot(features, depth=ATOM_DIM, axis=2)
return [
graph_to_molecule([adjacency[i].numpy(), features[i].numpy()])
for i in range(batch_size)
]
def call(self, inputs):
z_mean, log_var = self.encoder(inputs)
z = Sampling()([z_mean, log_var])
gen_adjacency, gen_features = self.decoder(z)
property_pred = self.property_prediction_layer(z_mean)
return z_mean, log_var, property_pred, gen_adjacency, gen_features
训练模型
vae_optimizer = tf.keras.optimizers.Adam(learning_rate=VAE_LR)
encoder = get_encoder(
gconv_units=[9],
adjacency_shape=(BOND_DIM, NUM_ATOMS, NUM_ATOMS),
feature_shape=(NUM_ATOMS, ATOM_DIM),
latent_dim=LATENT_DIM,
dense_units=[512],
dropout_rate=0.0,
)
decoder = get_decoder(
dense_units=[128, 256, 512],
dropout_rate=0.2,
latent_dim=LATENT_DIM,
adjacency_shape=(BOND_DIM, NUM_ATOMS, NUM_ATOMS),
feature_shape=(NUM_ATOMS, ATOM_DIM),
)
model = MoleculeGenerator(encoder, decoder, MAX_MOLSIZE)
model.compile(vae_optimizer)
history = model.fit([adjacency_tensor, feature_tensor, qed_tensor], epochs=EPOCHS)
第1/10轮
250/250 [==============================] - 24s 84ms/step - 损失: 68958.3946
第2/10轮
250/250 [==============================] - 20s 79ms/step - 损失: 68819.8421
第3/10轮
250/250 [==============================] - 20s 79ms/step - 损失: 68830.6720
第4/10轮
250/250 [==============================] - 20s 79ms/step - 损失: 68816.1486
第5/10轮
250/250 [==============================] - 20s 79ms/step - 损失: 68825.9977
第6/10轮
250/250 [==============================] - 19s 78ms/step - 损失: 68818.0771
第7/10轮
250/250 [==============================] - 19s 77ms/step - 损失: 68815.8525
第8/10轮
250/250 [==============================] - 20s 78ms/step - 损失: 68820.5459
第9/10轮
250/250 [==============================] - 21s 83ms/step - 损失: 68806.9465
第10/10轮
250/250 [==============================] - 21s 84ms/step - 损失: 68805.9879
推理
我们使用我们的模型从潜在空间中的不同点生成新的有效分子。
使用模型生成独特的分子
molecules = model.inference(1000)
MolsToGridImage(
[m for m in molecules if m is not None][:1000], molsPerRow=5, subImgSize=(260, 160)
)
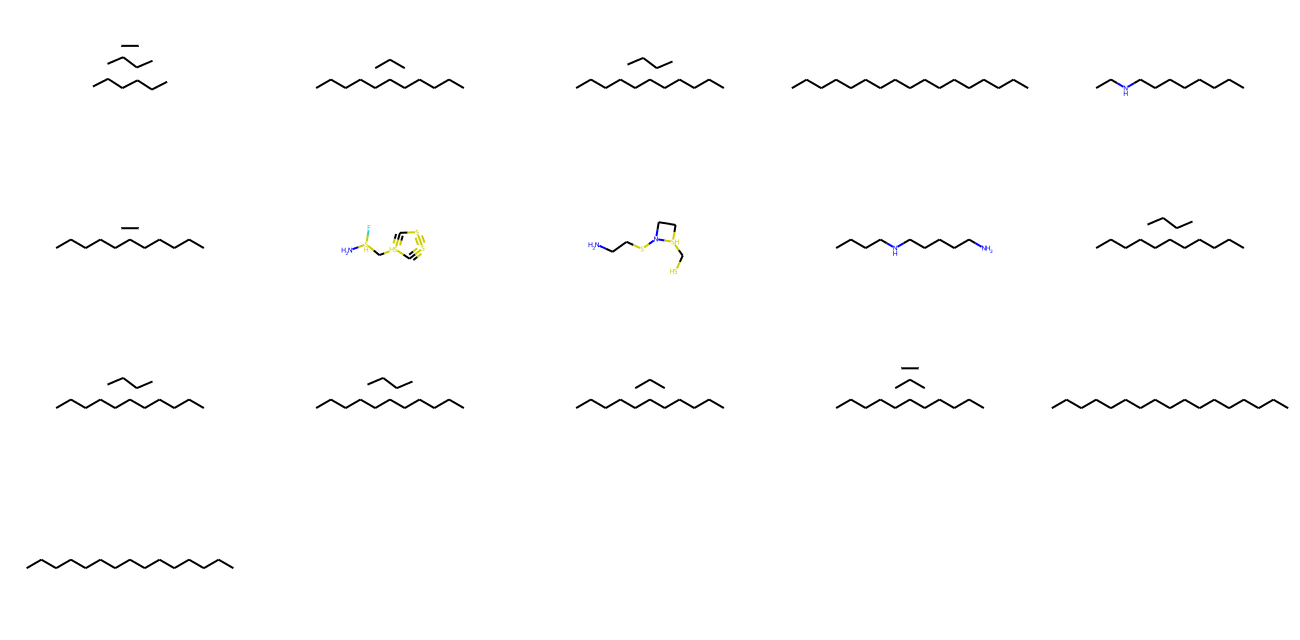
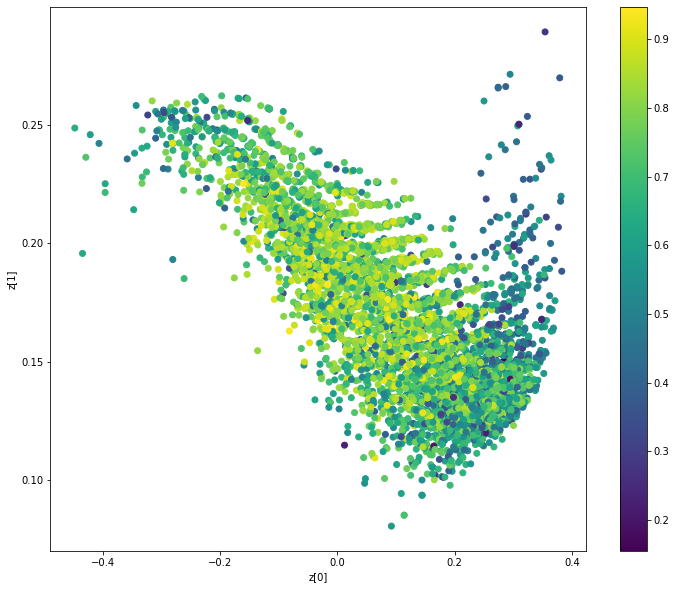
显示与分子特性(QAE)相关的潜在空间聚类
def plot_latent(vae, data, labels):
# 在潜在空间中显示属性的2D图
z_mean, _ = vae.encoder.predict(data)
plt.figure(figsize=(12, 10))
plt.scatter(z_mean[:, 0], z_mean[:, 1], c=labels)
plt.colorbar()
plt.xlabel("z[0]")
plt.ylabel("z[1]")
plt.show()
plot_latent(model, [adjacency_tensor[:8000], feature_tensor[:8000]], qed_tensor[:8000])
结论
在这个示例中,我们结合了来自两篇论文的模型架构, 2016年的“使用数据驱动的连续分子表示进行自动化化学设计”和2018年的“MolGAN”论文。前者将SMILES输入视为字符串,并试图生成SMILES格式的分子字符串, 而后者将SMILES输入视为图(邻接矩阵和特征矩阵的组合),并试图将分子作为图生成。
这种混合方法使得能够以一种新的方式在化学空间中进行定向梯度搜索。
示例可在HuggingFace上获取
| 训练模型 | 演示 |
|---|---|
 |
 |
