使用Real NVP的密度估计
作者: Mandolini Giorgio Maria, Sanna Daniele, Zannini Quirini Giorgio
创建日期: 2020/08/10
最后修改: 2020/08/10
描述: 估计"双月亮"数据集的密度分布。
介绍
本工作的目的是将一个简单的分布 - 易于采样且其密度易于估计 - 映射到一个更复杂的、从数据中学习的分布。这种生成模型也被称为"归一化流"。
为了实现这一点,模型通过最大似然原理进行训练,使用"变量变换"公式。
我们将使用一个仿射耦合函数。我们将其创建为其逆以及雅可比行列式易于获得(更多细节请参见引用的论文)。
要求:
- Tensorflow 2.9.1
- Tensorflow probability 0.17.0
参考文献:
设置
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers
from sklearn.datasets import make_moons
import numpy as np
import matplotlib.pyplot as plt
import tensorflow_probability as tfp
加载数据
data = make_moons(3000, noise=0.05)[0].astype("float32")
norm = layers.Normalization()
norm.adapt(data)
normalized_data = norm(data)
仿射耦合层
# 使用keras API创建自定义层。
output_dim = 256
reg = 0.01
def Coupling(input_shape):
input = keras.layers.Input(shape=input_shape)
t_layer_1 = keras.layers.Dense(
output_dim, activation="relu", kernel_regularizer=regularizers.l2(reg)
)(input)
t_layer_2 = keras.layers.Dense(
output_dim, activation="relu", kernel_regularizer=regularizers.l2(reg)
)(t_layer_1)
t_layer_3 = keras.layers.Dense(
output_dim, activation="relu", kernel_regularizer=regularizers.l2(reg)
)(t_layer_2)
t_layer_4 = keras.layers.Dense(
output_dim, activation="relu", kernel_regularizer=regularizers.l2(reg)
)(t_layer_3)
t_layer_5 = keras.layers.Dense(
input_shape, activation="linear", kernel_regularizer=regularizers.l2(reg)
)(t_layer_4)
s_layer_1 = keras.layers.Dense(
output_dim, activation="relu", kernel_regularizer=regularizers.l2(reg)
)(input)
s_layer_2 = keras.layers.Dense(
output_dim, activation="relu", kernel_regularizer=regularizers.l2(reg)
)(s_layer_1)
s_layer_3 = keras.layers.Dense(
output_dim, activation="relu", kernel_regularizer=regularizers.l2(reg)
)(s_layer_2)
s_layer_4 = keras.layers.Dense(
output_dim, activation="relu", kernel_regularizer=regularizers.l2(reg)
)(s_layer_3)
s_layer_5 = keras.layers.Dense(
input_shape, activation="tanh", kernel_regularizer=regularizers.l2(reg)
)(s_layer_4)
return keras.Model(inputs=input, outputs=[s_layer_5, t_layer_5])
Real NVP
class RealNVP(keras.Model):
def __init__(self, num_coupling_layers):
super().__init__()
self.num_coupling_layers = num_coupling_layers
# 潜在空间的分布。
self.distribution = tfp.distributions.MultivariateNormalDiag(
loc=[0.0, 0.0], scale_diag=[1.0, 1.0]
)
self.masks = np.array(
[[0, 1], [1, 0]] * (num_coupling_layers // 2), dtype="float32"
)
self.loss_tracker = keras.metrics.Mean(name="loss")
self.layers_list = [Coupling(2) for i in range(num_coupling_layers)]
@property
def metrics(self):
"""模型指标的列表。
我们确保损失跟踪器被列为`model.metrics`的一部分,
以便`fit()`和`evaluate()`能够在每个epoch开始时和`evaluate()`调用开始时
`reset()`损失跟踪器。
"""
return [self.loss_tracker]
def call(self, x, training=True):
log_det_inv = 0
direction = 1
if training:
direction = -1
for i in range(self.num_coupling_layers)[::direction]:
x_masked = x * self.masks[i]
reversed_mask = 1 - self.masks[i]
s, t = self.layers_list[i](x_masked)
s *= reversed_mask
t *= reversed_mask
gate = (direction - 1) / 2
x = (
reversed_mask
* (x * tf.exp(direction * s) + direction * t * tf.exp(gate * s))
+ x_masked
)
log_det_inv += gate * tf.reduce_sum(s, [1])
return x, log_det_inv
# 正态分布的对数似然加上雅可比的对数行列式。
def log_loss(self, x):
y, logdet = self(x)
log_likelihood = self.distribution.log_prob(y) + logdet
return -tf.reduce_mean(log_likelihood)
def train_step(self, data):
with tf.GradientTape() as tape:
loss = self.log_loss(data)
g = tape.gradient(loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(g, self.trainable_variables))
self.loss_tracker.update_state(loss)
return {"loss": self.loss_tracker.result()}
def test_step(self, data):
loss = self.log_loss(data)
self.loss_tracker.update_state(loss)
return {"loss": self.loss_tracker.result()}
模型训练
model = RealNVP(num_coupling_layers=6)
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.0001))
history = model.fit(
normalized_data, batch_size=256, epochs=300, verbose=2, validation_split=0.2
)
Epoch 1/300
10/10 - 2s - loss: 2.7104 - val_loss: 2.6385 - 2s/epoch - 248ms/step
Epoch 2/300
10/10 - 0s - loss: 2.5951 - val_loss: 2.5818 - 162ms/epoch - 16ms/step
Epoch 3/300
10/10 - 0s - loss: 2.5487 - val_loss: 2.5299 - 165ms/epoch - 17ms/step
Epoch 4/300
10/10 - 0s - loss: 2.5081 - val_loss: 2.4989 - 150ms/epoch - 15ms/step
Epoch 5/300
10/10 - 0s - loss: 2.4729 - val_loss: 2.4641 - 168ms/epoch - 17ms/step
Epoch 6/300
10/10 - 0s - loss: 2.4457 - val_loss: 2.4443 - 155ms/epoch - 16ms/step
Epoch 7/300
10/10 - 0s - loss: 2.4183 - val_loss: 2.4078 - 155ms/epoch - 16ms/step
Epoch 8/300
10/10 - 0s - loss: 2.3840 - val_loss: 2.3852 - 160ms/epoch - 16ms/step
Epoch 9/300
10/10 - 0s - loss: 2.3604 - val_loss: 2.3700 - 172ms/epoch - 17ms/step
Epoch 10/300
10/10 - 0s - loss: 2.3392 - val_loss: 2.3354 - 156ms/epoch - 16ms/step
Epoch 11/300
10/10 - 0s - loss: 2.3042 - val_loss: 2.3099 - 170ms/epoch - 17ms/step
Epoch 12/300
10/10 - 0s - loss: 2.2769 - val_loss: 2.3126 - 171ms/epoch - 17ms/step
Epoch 13/300
10/10 - 0s - loss: 2.2541 - val_loss: 2.2784 - 174ms/epoch - 17ms/step
Epoch 14/300
10/10 - 0s - loss: 2.2175 - val_loss: 2.2354 - 174ms/epoch - 17ms/step
Epoch 15/300
10/10 - 0s - loss: 2.1957 - val_loss: 2.1990 - 173ms/epoch - 17ms/step
Epoch 16/300
10/10 - 0s - loss: 2.1533 - val_loss: 2.1686 - 167ms/epoch - 17ms/step
Epoch 17/300
10/10 - 0s - loss: 2.1232 - val_loss: 2.1276 - 178ms/epoch - 18ms/step
Epoch 18/300
10/10 - 0s - loss: 2.0932 - val_loss: 2.1220 - 173ms/epoch - 17ms/step
Epoch 19/300
10/10 - 0s - loss: 2.1068 - val_loss: 2.1515 - 152ms/epoch - 15ms/step
Epoch 20/300
10/10 - 0s - loss: 2.0793 - val_loss: 2.1661 - 161ms/epoch - 16ms/step
Epoch 21/300
10/10 - 0s - loss: 2.0784 - val_loss: 2.0634 - 180ms/epoch - 18ms/step
Epoch 22/300
10/10 - 0s - loss: 2.0060 - val_loss: 2.0076 - 160ms/epoch - 16ms/step
Epoch 23/300
10/10 - 0s - loss: 1.9845 - val_loss: 1.9773 - 174ms/epoch - 17ms/step
Epoch 24/300
10/10 - 0s - loss: 1.9462 - val_loss: 2.0097 - 174ms/epoch - 17ms/step
Epoch 25/300
10/10 - 0s - loss: 1.8892 - val_loss: 1.9023 - 173ms/epoch - 17ms/step
Epoch 26/300
10/10 - 0s - loss: 1.8011 - val_loss: 1.8128 - 182ms/epoch - 18ms/step
Epoch 27/300
10/10 - 0s - loss: 1.7604 - val_loss: 1.8415 - 167ms/epoch - 17ms/step
Epoch 28/300
10/10 - 0s - loss: 1.7474 - val_loss: 1.7635 - 172ms/epoch - 17ms/step
Epoch 29/300
10/10 - 0s - loss: 1.7313 - val_loss: 1.7154 - 175ms/epoch - 18ms/step
Epoch 30/300
10/10 - 0s - loss: 1.6801 - val_loss: 1.7269 - 183ms/epoch - 18ms/step
Epoch 31/300
10/10 - 0s - loss: 1.6892 - val_loss: 1.6588 - 170ms/epoch - 17ms/step
Epoch 32/300
10/10 - 0s - loss: 1.6384 - val_loss: 1.6467 - 159ms/epoch - 16ms/step
Epoch 33/300
10/10 - 0s - loss: 1.6263 - val_loss: 1.6214 - 164ms/epoch - 16ms/step
Epoch 34/300
10/10 - 0s - loss: 1.6035 - val_loss: 1.6022 - 154ms/epoch - 15ms/step
Epoch 35/300
10/10 - 0s - loss: 1.5872 - val_loss: 1.6203 - 159ms/epoch - 16ms/step
Epoch 36/300
10/10 - 0s - loss: 1.5928 - val_loss: 1.6312 - 159ms/epoch - 16ms/step
Epoch 37/300
10/10 - 0s - loss: 1.5895 - val_loss: 1.6337 - 148ms/epoch - 15ms/step
Epoch 38/300
10/10 - 0s - loss: 1.5726 - val_loss: 1.6192 - 153ms/epoch - 15ms/step
Epoch 39/300
10/10 - 0s - loss: 1.5537 - val_loss: 1.5919 - 168ms/epoch - 17ms/step
Epoch 40/300
10/10 - 0s - loss: 1.5741 - val_loss: 1.6646 - 173ms/epoch - 17ms/step
Epoch 41/300
10/10 - 0s - loss: 1.5737 - val_loss: 1.5718 - 181ms/epoch - 18ms/step
Epoch 42/300
10/10 - 0s - loss: 1.5573 - val_loss: 1.6395 - 173ms/epoch - 17ms/step
Epoch 43/300
10/10 - 0s - loss: 1.5574 - val_loss: 1.5779 - 183ms/epoch - 18ms/step
Epoch 44/300
10/10 - 0s - loss: 1.5345 - val_loss: 1.5549 - 173ms/epoch - 17ms/step
Epoch 45/300
10/10 - 0s - loss: 1.5256 - val_loss: 1.5944 - 161ms/epoch - 16ms/step
Epoch 46/300
10/10 - 0s - loss: 1.5291 - val_loss: 1.5325 - 169ms/epoch - 17ms/step
Epoch 47/300
10/10 - 0s - loss: 1.5341 - val_loss: 1.5929 - 177ms/epoch - 18ms/step
Epoch 48/300
10/10 - 0s - loss: 1.5190 - val_loss: 1.5563 - 174ms/epoch - 17ms/step
Epoch 49/300
10/10 - 0s - loss: 1.5059 - val_loss: 1.5079 - 187ms/epoch - 19ms/step
Epoch 50/300
10/10 - 0s - loss: 1.4971 - val_loss: 1.5163 - 177ms/epoch - 18ms/step
Epoch 51/300
10/10 - 0s - loss: 1.4923 - val_loss: 1.5549 - 168ms/epoch - 17ms/step
Epoch 52/300
10/10 - 0s - loss: 1.5345 - val_loss: 1.7131 - 171ms/epoch - 17ms/step
Epoch 53/300
10/10 - 0s - loss: 1.5381 - val_loss: 1.5102 - 174ms/epoch - 17ms/step
Epoch 54/300
10/10 - 0s - loss: 1.4955 - val_loss: 1.5432 - 167ms/epoch - 17ms/step
Epoch 55/300
10/10 - 0s - loss: 1.4829 - val_loss: 1.5166 - 172ms/epoch - 17ms/step
Epoch 56/300
10/10 - 0s - loss: 1.4672 - val_loss: 1.5297 - 180ms/epoch - 18ms/step
Epoch 57/300
10/10 - 0s - loss: 1.4814 - val_loss: 1.5115 - 166ms/epoch - 17ms/step
Epoch 58/300
10/10 - 0s - loss: 1.4738 - val_loss: 1.5143 - 165ms/epoch - 17ms/step
Epoch 59/300
10/10 - 0s - loss: 1.4639 - val_loss: 1.5326 - 175ms/epoch - 17ms/step
Epoch 60/300
10/10 - 0s - loss: 1.4727 - val_loss: 1.5419 - 175ms/epoch - 18ms/step
Epoch 61/300
10/10 - 0s - loss: 1.4610 - val_loss: 1.4663 - 177ms/epoch - 18ms/step
Epoch 62/300
10/10 - 0s - loss: 1.4512 - val_loss: 1.5624 - 179ms/epoch - 18ms/step
Epoch 63/300
10/10 - 0s - loss: 1.4816 - val_loss: 1.5711 - 176ms/epoch - 18ms/step
Epoch 64/300
10/10 - 0s - loss: 1.4735 - val_loss: 1.4988 - 181ms/epoch - 18ms/step
Epoch 65/300
10/10 - 0s - loss: 1.4443 - val_loss: 1.4850 - 185ms/epoch - 19ms/step
Epoch 66/300
10/10 - 0s - loss: 1.4441 - val_loss: 1.5275 - 179ms/epoch - 18ms/step
Epoch 67/300
10/10 - 0s - loss: 1.4751 - val_loss: 1.5191 - 177ms/epoch - 18ms/step
Epoch 68/300
10/10 - 0s - loss: 1.4874 - val_loss: 1.4888 - 175ms/epoch - 18ms/step
Epoch 69/300
10/10 - 0s - loss: 1.4442 - val_loss: 1.5044 - 167ms/epoch - 17ms/step
Epoch 70/300
10/10 - 0s - loss: 1.4645 - val_loss: 1.4801 - 174ms/epoch - 17ms/step
Epoch 71/300
10/10 - 0s - loss: 1.4648 - val_loss: 1.5016 - 174ms/epoch - 17ms/step
Epoch 72/300
10/10 - 0s - loss: 1.4336 - val_loss: 1.4970 - 171ms/epoch - 17ms/step
Epoch 73/300
10/10 - 0s - loss: 1.4852 - val_loss: 1.4561 - 176ms/epoch - 18ms/step
Epoch 74/300
10/10 - 0s - loss: 1.4656 - val_loss: 1.5156 - 167ms/epoch - 17ms/step
Epoch 75/300
10/10 - 0s - loss: 1.4359 - val_loss: 1.4154 - 175ms/epoch - 17ms/step
Epoch 76/300
10/10 - 0s - loss: 1.5187 - val_loss: 1.5395 - 182ms/epoch - 18ms/step
Epoch 77/300
10/10 - 0s - loss: 1.5554 - val_loss: 1.5524 - 179ms/epoch - 18ms/step
Epoch 78/300
10/10 - 0s - loss: 1.4679 - val_loss: 1.4742 - 175ms/epoch - 18ms/step
Epoch 79/300
10/10 - 0s - loss: 1.4433 - val_loss: 1.5862 - 177ms/epoch - 18ms/step
Epoch 80/300
10/10 - 0s - loss: 1.4775 - val_loss: 1.5030 - 189ms/epoch - 19ms/step
Epoch 81/300
10/10 - 0s - loss: 1.4020 - val_loss: 1.5264 - 169ms/epoch - 17ms/step
Epoch 82/300
10/10 - 0s - loss: 1.4298 - val_loss: 1.4841 - 170ms/epoch - 17ms/step
Epoch 83/300
10/10 - 0s - loss: 1.4329 - val_loss: 1.3966 - 177ms/epoch - 18ms/step
Epoch 84/300
10/10 - 0s - loss: 1.4106 - val_loss: 1.4472 - 183ms/epoch - 18ms/step
Epoch 85/300
10/10 - 0s - loss: 1.3902 - val_loss: 1.5917 - 174ms/epoch - 17ms/step
Epoch 86/300
10/10 - 0s - loss: 1.6401 - val_loss: 1.6188 - 181ms/epoch - 18ms/step
Epoch 87/300
10/10 - 0s - loss: 1.5748 - val_loss: 1.5913 - 177ms/epoch - 18ms/step
Epoch 88/300
10/10 - 0s - loss: 1.5449 - val_loss: 1.5437 - 185ms/epoch - 19ms/step
Epoch 89/300
10/10 - 0s - loss: 1.4769 - val_loss: 1.5344 - 185ms/epoch - 19ms/step
Epoch 90/300
10/10 - 0s - loss: 1.4805 - val_loss: 1.4814 - 173ms/epoch - 17ms/step
Epoch 91/300
10/10 - 0s - loss: 1.4540 - val_loss: 1.5087 - 170ms/epoch - 17ms/step
Epoch 92/300
10/10 - 0s - loss: 1.4266 - val_loss: 1.4554 - 169ms/epoch - 17ms/step
Epoch 93/300
10/10 - 0s - loss: 1.4014 - val_loss: 1.4492 - 185ms/epoch - 19ms/step
Epoch 94/300
10/10 - 0s - loss: 1.3701 - val_loss: 1.3875 - 182ms/epoch - 18ms/step
Epoch 95/300
10/10 - 0s - loss: 1.3792 - val_loss: 1.4288 - 193ms/epoch - 19ms/step
Epoch 96/300
10/10 - 0s - loss: 1.3813 - val_loss: 1.4452 - 180ms/epoch - 18ms/step
Epoch 97/300
10/10 - 0s - loss: 1.3505 - val_loss: 1.3954 - 173ms/epoch - 17ms/step
Epoch 98/300
10/10 - 0s - loss: 1.3870 - val_loss: 1.6328 - 178ms/epoch - 18ms/step
Epoch 99/300
10/10 - 0s - loss: 1.5100 - val_loss: 1.5139 - 174ms/epoch - 17ms/step
Epoch 100/300
10/10 - 0s - loss: 1.4355 - val_loss: 1.4654 - 176ms/epoch - 18ms/step
Epoch 101/300
10/10 - 0s - loss: 1.3967 - val_loss: 1.4168 - 156ms/epoch - 16ms/step
Epoch 102/300
10/10 - 0s - loss: 1.3466 - val_loss: 1.3765 - 164ms/epoch - 16ms/step
Epoch 103/300
10/10 - 0s - loss: 1.3188 - val_loss: 1.3783 - 182ms/epoch - 18ms/step
Epoch 104/300
10/10 - 0s - loss: 1.3659 - val_loss: 1.4572 - 190ms/epoch - 19ms/step
Epoch 105/300
10/10 - 0s - loss: 1.6089 - val_loss: 1.6353 - 184ms/epoch - 18ms/step
Epoch 106/300
10/10 - 0s - loss: 1.6317 - val_loss: 1.6007 - 171ms/epoch - 17ms/step
Epoch 107/300
10/10 - 0s - loss: 1.5652 - val_loss: 1.5409 - 184ms/epoch - 18ms/step
Epoch 108/300
10/10 - 0s - loss: 1.5273 - val_loss: 1.5030 - 165ms/epoch - 17ms/step
Epoch 109/300
10/10 - 0s - loss: 1.4750 - val_loss: 1.4796 - 179ms/epoch - 18ms/step
Epoch 110/300
10/10 - 0s - loss: 1.4710 - val_loss: 1.4996 - 175ms/epoch - 18ms/step
Epoch 111/300
10/10 - 0s - loss: 1.4805 - val_loss: 1.5006 - 179ms/epoch - 18ms/step
Epoch 112/300
10/10 - 0s - loss: 1.4518 - val_loss: 1.5023 - 184ms/epoch - 18ms/step
Epoch 113/300
10/10 - 0s - loss: 1.4313 - val_loss: 1.4234 - 162ms/epoch - 16ms/step
Epoch 114/300
10/10 - 0s - loss: 1.4113 - val_loss: 1.4629 - 178ms/epoch - 18ms/step
Epoch 115/300
10/10 - 0s - loss: 1.3999 - val_loss: 1.4300 - 170ms/epoch - 17ms/step
Epoch 116/300
10/10 - 0s - loss: 1.3886 - val_loss: 1.4042 - 179ms/epoch - 18ms/step
Epoch 117/300
10/10 - 0s - loss: 1.3659 - val_loss: 1.4245 - 182ms/epoch - 18ms/step
Epoch 118/300
10/10 - 0s - loss: 1.3605 - val_loss: 1.4482 - 162ms/epoch - 16ms/step
Epoch 119/300
10/10 - 0s - loss: 1.4003 - val_loss: 1.4756 - 163ms/epoch - 16ms/step
Epoch 120/300
10/10 - 0s - loss: 1.3749 - val_loss: 1.4237 - 189ms/epoch - 19ms/step
Epoch 121/300
10/10 - 0s - loss: 1.3323 - val_loss: 1.3580 - 189ms/epoch - 19ms/step
Epoch 122/300
10/10 - 0s - loss: 1.3464 - val_loss: 1.3684 - 187ms/epoch - 19ms/step
Epoch 123/300
10/10 - 0s - loss: 1.3430 - val_loss: 1.3345 - 183ms/epoch - 18ms/step
Epoch 124/300
10/10 - 0s - loss: 1.3402 - val_loss: 1.4077 - 183ms/epoch - 18ms/step
Epoch 125/300
10/10 - 0s - loss: 1.3861 - val_loss: 1.4208 - 165ms/epoch - 17ms/step
Epoch 126/300
10/10 - 0s - loss: 1.3665 - val_loss: 1.4796 - 163ms/epoch - 16ms/step
Epoch 127/300
10/10 - 0s - loss: 1.3912 - val_loss: 1.4770 - 169ms/epoch - 17ms/step
Epoch 128/300
10/10 - 0s - loss: 1.4114 - val_loss: 1.4261 - 166ms/epoch - 17ms/step
Epoch 129/300
10/10 - 0s - loss: 1.3687 - val_loss: 1.4488 - 165ms/epoch - 17ms/step
Epoch 130/300
10/10 - 0s - loss: 1.3576 - val_loss: 1.4333 - 173ms/epoch - 17ms/step
Epoch 131/300
10/10 - 0s - loss: 1.3413 - val_loss: 1.4298 - 180ms/epoch - 18ms/step
Epoch 132/300
10/10 - 0s - loss: 1.3331 - val_loss: 1.4388 - 190ms/epoch - 19ms/step
Epoch 133/300
10/10 - 0s - loss: 1.5913 - val_loss: 1.5962 - 188ms/epoch - 19ms/step
Epoch 134/300
10/10 - 0s - loss: 1.6076 - val_loss: 1.5921 - 179ms/epoch - 18ms/step
Epoch 135/300
10/10 - 0s - loss: 1.5387 - val_loss: 1.5856 - 183ms/epoch - 18ms/step
Epoch 136/300
10/10 - 0s - loss: 1.5088 - val_loss: 1.5209 - 159ms/epoch - 16ms/step
Epoch 137/300
10/10 - 0s - loss: 1.4640 - val_loss: 1.4599 - 175ms/epoch - 18ms/step
Epoch 138/300
10/10 - 0s - loss: 1.4140 - val_loss: 1.4659 - 177ms/epoch - 18ms/step
Epoch 139/300
10/10 - 0s - loss: 1.4138 - val_loss: 1.4327 - 179ms/epoch - 18ms/step
Epoch 140/300
10/10 - 0s - loss: 1.3911 - val_loss: 1.4366 - 178ms/epoch - 18ms/step
Epoch 141/300
10/10 - 0s - loss: 1.3870 - val_loss: 1.3962 - 182ms/epoch - 18ms/step
Epoch 142/300
10/10 - 0s - loss: 1.3699 - val_loss: 1.4742 - 154ms/epoch - 15ms/step
Epoch 143/300
10/10 - 0s - loss: 1.3630 - val_loss: 1.3963 - 158ms/epoch - 16ms/step
Epoch 144/300
10/10 - 0s - loss: 1.3818 - val_loss: 1.4538 - 184ms/epoch - 18ms/step
Epoch 145/300
10/10 - 0s - loss: 1.3564 - val_loss: 1.4057 - 182ms/epoch - 18ms/step
Epoch 146/300
10/10 - 0s - loss: 1.3353 - val_loss: 1.4064 - 186ms/epoch - 19ms/step
Epoch 147/300
10/10 - 0s - loss: 1.3285 - val_loss: 1.3835 - 172ms/epoch - 17ms/step
Epoch 148/300
10/10 - 0s - loss: 1.3100 - val_loss: 1.3817 - 188ms/epoch - 19ms/step
Epoch 149/300
10/10 - 0s - loss: 1.3761 - val_loss: 1.4566 - 189ms/epoch - 19ms/step
Epoch 150/300
10/10 - 0s - loss: 1.3473 - val_loss: 1.4378 - 188ms/epoch - 19ms/step
Epoch 151/300
10/10 - 0s - loss: 1.3106 - val_loss: 1.3616 - 182ms/epoch - 18ms/step
Epoch 152/300
10/10 - 0s - loss: 1.3239 - val_loss: 1.3468 - 177ms/epoch - 18ms/step
Epoch 153/300
10/10 - 0s - loss: 1.2947 - val_loss: 1.3523 - 172ms/epoch - 17ms/step
Epoch 154/300
10/10 - 0s - loss: 1.2850 - val_loss: 1.3530 - 170ms/epoch - 17ms/step
Epoch 155/300
10/10 - 0s - loss: 1.2834 - val_loss: 1.3878 - 171ms/epoch - 17ms/step
Epoch 156/300
10/10 - 0s - loss: 1.3192 - val_loss: 1.3747 - 179ms/epoch - 18ms/step
Epoch 157/300
10/10 - 0s - loss: 1.3567 - val_loss: 1.4031 - 174ms/epoch - 17ms/step
Epoch 158/300
10/10 - 0s - loss: 1.3240 - val_loss: 1.3735 - 167ms/epoch - 17ms/step
Epoch 159/300
10/10 - 0s - loss: 1.3272 - val_loss: 1.4563 - 183ms/epoch - 18ms/step
Epoch 160/300
10/10 - 0s - loss: 1.3329 - val_loss: 1.3321 - 179ms/epoch - 18ms/step
Epoch 161/300
10/10 - 0s - loss: 1.3120 - val_loss: 1.3779 - 185ms/epoch - 19ms/step
Epoch 162/300
10/10 - 0s - loss: 1.3093 - val_loss: 1.3739 - 191ms/epoch - 19ms/step
Epoch 163/300
10/10 - 0s - loss: 1.3251 - val_loss: 1.4781 - 182ms/epoch - 18ms/step
Epoch 164/300
10/10 - 0s - loss: 1.3762 - val_loss: 1.4035 - 165ms/epoch - 17ms/step
Epoch 165/300
10/10 - 0s - loss: 1.3655 - val_loss: 1.3693 - 189ms/epoch - 19ms/step
Epoch 166/300
10/10 - 0s - loss: 1.3453 - val_loss: 1.3694 - 170ms/epoch - 17ms/step
Epoch 167/300
10/10 - 0s - loss: 1.3019 - val_loss: 1.3496 - 180ms/epoch - 18ms/step
Epoch 168/300
10/10 - 0s - loss: 1.2801 - val_loss: 1.3375 - 190ms/epoch - 19ms/step
Epoch 169/300
10/10 - 0s - loss: 1.2966 - val_loss: 1.3712 - 178ms/epoch - 18ms/step
Epoch 170/300
10/10 - 0s - loss: 1.3060 - val_loss: 1.3237 - 177ms/epoch - 18ms/step
Epoch 171/300
10/10 - 0s - loss: 1.3299 - val_loss: 1.5022 - 177ms/epoch - 18ms/step
Epoch 172/300
10/10 - 0s - loss: 1.3665 - val_loss: 1.4224 - 186ms/epoch - 19ms/step
Epoch 173/300
10/10 - 0s - loss: 1.3432 - val_loss: 1.5198 - 172ms/epoch - 17ms/step
Epoch 174/300
10/10 - 0s - loss: 1.3434 - val_loss: 1.4113 - 188ms/epoch - 19ms/step
Epoch 175/300
10/10 - 0s - loss: 1.3016 - val_loss: 1.3920 - 175ms/epoch - 18ms/step
Epoch 176/300
10/10 - 0s - loss: 1.2833 - val_loss: 1.4342 - 166ms/epoch - 17ms/step
Epoch 177/300
10/10 - 0s - loss: 1.3334 - val_loss: 1.4225 - 178ms/epoch - 18ms/step
Epoch 178/300
10/10 - 0s - loss: 1.4085 - val_loss: 1.4848 - 170ms/epoch - 17ms/step
Epoch 179/300
10/10 - 0s - loss: 1.4262 - val_loss: 1.5149 - 176ms/epoch - 18ms/step
Epoch 180/300
10/10 - 0s - loss: 1.4076 - val_loss: 1.5736 - 175ms/epoch - 18ms/step
Epoch 181/300
10/10 - 0s - loss: 1.5085 - val_loss: 1.6339 - 179ms/epoch - 18ms/step
Epoch 182/300
10/10 - 0s - loss: 1.5028 - val_loss: 1.5327 - 179ms/epoch - 18ms/step
Epoch 183/300
10/10 - 0s - loss: 1.4710 - val_loss: 1.4611 - 196ms/epoch - 20ms/step
Epoch 184/300
10/10 - 0s - loss: 1.3950 - val_loss: 1.4205 - 190ms/epoch - 19ms/step
Epoch 185/300
10/10 - 0s - loss: 1.3815 - val_loss: 1.4100 - 187ms/epoch - 19ms/step
Epoch 186/300
10/10 - 0s - loss: 1.3722 - val_loss: 1.3939 - 163ms/epoch - 16ms/step
Epoch 187/300
10/10 - 0s - loss: 1.3379 - val_loss: 1.3922 - 194ms/epoch - 19ms/step
Epoch 188/300
10/10 - 0s - loss: 1.3406 - val_loss: 1.3874 - 189ms/epoch - 19ms/step
Epoch 189/300
10/10 - 0s - loss: 1.4787 - val_loss: 1.5603 - 190ms/epoch - 19ms/step
Epoch 190/300
10/10 - 0s - loss: 1.4652 - val_loss: 1.4490 - 163ms/epoch - 16ms/step
Epoch 191/300
10/10 - 0s - loss: 1.3868 - val_loss: 1.4725 - 179ms/epoch - 18ms/step
Epoch 192/300
10/10 - 0s - loss: 1.3470 - val_loss: 1.4088 - 186ms/epoch - 19ms/step
Epoch 193/300
10/10 - 0s - loss: 1.3576 - val_loss: 1.3549 - 193ms/epoch - 19ms/step
Epoch 194/300
10/10 - 0s - loss: 1.3574 - val_loss: 1.4884 - 188ms/epoch - 19ms/step
Epoch 195/300
10/10 - 0s - loss: 1.4376 - val_loss: 1.4794 - 172ms/epoch - 17ms/step
Epoch 196/300
10/10 - 0s - loss: 1.4110 - val_loss: 1.5064 - 175ms/epoch - 18ms/step
Epoch 197/300
10/10 - 0s - loss: 1.3597 - val_loss: 1.3742 - 159ms/epoch - 16ms/step
Epoch 198/300
10/10 - 0s - loss: 1.3897 - val_loss: 1.4465 - 188ms/epoch - 19ms/step
Epoch 199/300
10/10 - 0s - loss: 1.3710 - val_loss: 1.3469 - 175ms/epoch - 18ms/step
Epoch 200/300
10/10 - 0s - loss: 1.3613 - val_loss: 1.4129 - 183ms/epoch - 18ms/step
Epoch 201/300
10/10 - 0s - loss: 1.3581 - val_loss: 1.4100 - 189ms/epoch - 19ms/step
Epoch 202/300
10/10 - 0s - loss: 1.3047 - val_loss: 1.3460 - 164ms/epoch - 16ms/step
Epoch 203/300
10/10 - 0s - loss: 1.3133 - val_loss: 1.3942 - 185ms/epoch - 18ms/step
Epoch 204/300
10/10 - 0s - loss: 1.3880 - val_loss: 1.4730 - 179ms/epoch - 18ms/step
Epoch 205/300
10/10 - 0s - loss: 1.4233 - val_loss: 1.5020 - 196ms/epoch - 20ms/step
Epoch 206/300
10/10 - 0s - loss: 1.3696 - val_loss: 1.4541 - 188ms/epoch - 19ms/step
Epoch 207/300
10/10 - 0s - loss: 1.3189 - val_loss: 1.4825 - 181ms/epoch - 18ms/step
Epoch 208/300
10/10 - 0s - loss: 1.7335 - val_loss: 1.7628 - 170ms/epoch - 17ms/step
Epoch 209/300
10/10 - 0s - loss: 1.6927 - val_loss: 1.6906 - 180ms/epoch - 18ms/step
Epoch 210/300
10/10 - 0s - loss: 1.6293 - val_loss: 1.6065 - 191ms/epoch - 19ms/step
Epoch 211/300
10/10 - 0s - loss: 1.5564 - val_loss: 1.5873 - 179ms/epoch - 18ms/step
Epoch 212/300
10/10 - 0s - loss: 1.5258 - val_loss: 1.5561 - 188ms/epoch - 19ms/step
Epoch 213/300
10/10 - 0s - loss: 1.4918 - val_loss: 1.5715 - 175ms/epoch - 17ms/step
Epoch 214/300
10/10 - 0s - loss: 1.4800 - val_loss: 1.5373 - 166ms/epoch - 17ms/step
Epoch 215/300
10/10 - 0s - loss: 1.4669 - val_loss: 1.5262 - 171ms/epoch - 17ms/step
Epoch 216/300
10/10 - 0s - loss: 1.4492 - val_loss: 1.4965 - 168ms/epoch - 17ms/step
Epoch 217/300
10/10 - 0s - loss: 1.4169 - val_loss: 1.4874 - 160ms/epoch - 16ms/step
Epoch 218/300
10/10 - 0s - loss: 1.4192 - val_loss: 1.4848 - 175ms/epoch - 18ms/step
Epoch 219/300
10/10 - 0s - loss: 1.4072 - val_loss: 1.4776 - 167ms/epoch - 17ms/step
Epoch 220/300
10/10 - 0s - loss: 1.3936 - val_loss: 1.4824 - 163ms/epoch - 16ms/step
Epoch 221/300
10/10 - 0s - loss: 1.3813 - val_loss: 1.4814 - 190ms/epoch - 19ms/step
Epoch 222/300
10/10 - 0s - loss: 1.3821 - val_loss: 1.4344 - 192ms/epoch - 19ms/step
Epoch 223/300
10/10 - 0s - loss: 1.3724 - val_loss: 1.4691 - 197ms/epoch - 20ms/step
Epoch 224/300
10/10 - 0s - loss: 1.3818 - val_loss: 1.4371 - 186ms/epoch - 19ms/step
Epoch 225/300
10/10 - 0s - loss: 1.3986 - val_loss: 1.4602 - 174ms/epoch - 17ms/step
Epoch 226/300
10/10 - 0s - loss: 1.3620 - val_loss: 1.4268 - 162ms/epoch - 16ms/step
Epoch 227/300
10/10 - 0s - loss: 1.3658 - val_loss: 1.5127 - 162ms/epoch - 16ms/step
Epoch 228/300
10/10 - 0s - loss: 1.3994 - val_loss: 1.4251 - 182ms/epoch - 18ms/step
Epoch 229/300
10/10 - 0s - loss: 1.3674 - val_loss: 1.4542 - 181ms/epoch - 18ms/step
Epoch 230/300
10/10 - 0s - loss: 1.3453 - val_loss: 1.4165 - 178ms/epoch - 18ms/step
Epoch 231/300
10/10 - 0s - loss: 1.3473 - val_loss: 1.4112 - 185ms/epoch - 19ms/step
Epoch 232/300
10/10 - 0s - loss: 1.3373 - val_loss: 1.3559 - 193ms/epoch - 19ms/step
Epoch 233/300
10/10 - 0s - loss: 1.3267 - val_loss: 1.4230 - 185ms/epoch - 19ms/step
Epoch 234/300
10/10 - 0s - loss: 1.4402 - val_loss: 1.5016 - 194ms/epoch - 19ms/step
Epoch 235/300
10/10 - 0s - loss: 1.4497 - val_loss: 1.5198 - 182ms/epoch - 18ms/step
Epoch 236/300
10/10 - 0s - loss: 1.3724 - val_loss: 1.4116 - 174ms/epoch - 17ms/step
Epoch 237/300
10/10 - 0s - loss: 1.3275 - val_loss: 1.4120 - 190ms/epoch - 19ms/step
Epoch 238/300
10/10 - 0s - loss: 1.4089 - val_loss: 1.4978 - 180ms/epoch - 18ms/step
Epoch 239/300
10/10 - 0s - loss: 1.4203 - val_loss: 1.4340 - 197ms/epoch - 20ms/step
Epoch 240/300
10/10 - 0s - loss: 1.4002 - val_loss: 1.4535 - 181ms/epoch - 18ms/step
Epoch 241/300
10/10 - 0s - loss: 1.3915 - val_loss: 1.4112 - 179ms/epoch - 18ms/step
Epoch 242/300
10/10 - 0s - loss: 1.4050 - val_loss: 1.4437 - 173ms/epoch - 17ms/step
Epoch 243/300
10/10 - 0s - loss: 1.3834 - val_loss: 1.3841 - 183ms/epoch - 18ms/step
Epoch 244/300
10/10 - 0s - loss: 1.3550 - val_loss: 1.4028 - 185ms/epoch - 19ms/step
Epoch 245/300
10/10 - 0s - loss: 1.3415 - val_loss: 1.4119 - 200ms/epoch - 20ms/step
Epoch 246/300
10/10 - 0s - loss: 1.3579 - val_loss: 1.4416 - 188ms/epoch - 19ms/step
Epoch 247/300
10/10 - 0s - loss: 1.3397 - val_loss: 1.4257 - 173ms/epoch - 17ms/step
Epoch 248/300
10/10 - 0s - loss: 1.3353 - val_loss: 1.3809 - 188ms/epoch - 19ms/step
Epoch 249/300
10/10 - 0s - loss: 1.3211 - val_loss: 1.3619 - 169ms/epoch - 17ms/step
Epoch 250/300
10/10 - 0s - loss: 1.3052 - val_loss: 1.3735 - 168ms/epoch - 17ms/step
Epoch 251/300
10/10 - 0s - loss: 1.3121 - val_loss: 1.3636 - 183ms/epoch - 18ms/step
Epoch 252/300
10/10 - 0s - loss: 1.3121 - val_loss: 1.3741 - 177ms/epoch - 18ms/step
Epoch 253/300
10/10 - 0s - loss: 1.3108 - val_loss: 1.3680 - 168ms/epoch - 17ms/step
Epoch 254/300
10/10 - 0s - loss: 1.3188 - val_loss: 1.4326 - 184ms/epoch - 18ms/step
Epoch 255/300
10/10 - 0s - loss: 1.3111 - val_loss: 1.3853 - 183ms/epoch - 18ms/step
Epoch 256/300
10/10 - 0s - loss: 1.3036 - val_loss: 1.4108 - 195ms/epoch - 20ms/step
Epoch 257/300
10/10 - 0s - loss: 1.2867 - val_loss: 1.3785 - 183ms/epoch - 18ms/step
Epoch 258/300
10/10 - 0s - loss: 1.2768 - val_loss: 1.3614 - 165ms/epoch - 17ms/step
Epoch 259/300
10/10 - 0s - loss: 1.3092 - val_loss: 1.3846 - 176ms/epoch - 18ms/step
Epoch 260/300
10/10 - 0s - loss: 1.2845 - val_loss: 1.3970 - 169ms/epoch - 17ms/step
Epoch 261/300
10/10 - 0s - loss: 1.3381 - val_loss: 1.3931 - 175ms/epoch - 18ms/step
Epoch 262/300
10/10 - 0s - loss: 1.3067 - val_loss: 1.3953 - 176ms/epoch - 18ms/step
Epoch 263/300
10/10 - 0s - loss: 1.2947 - val_loss: 1.3783 - 170ms/epoch - 17ms/step
Epoch 264/300
10/10 - 0s - loss: 1.2947 - val_loss: 1.3805 - 187ms/epoch - 19ms/step
Epoch 265/300
10/10 - 0s - loss: 1.3187 - val_loss: 1.3418 - 187ms/epoch - 19ms/step
Epoch 266/300
10/10 - 0s - loss: 1.2830 - val_loss: 1.4077 - 197ms/epoch - 20ms/step
Epoch 267/300
10/10 - 0s - loss: 1.3008 - val_loss: 1.3461 - 198ms/epoch - 20ms/step
Epoch 268/300
10/10 - 0s - loss: 1.3230 - val_loss: 1.3495 - 183ms/epoch - 18ms/step
Epoch 269/300
10/10 - 0s - loss: 1.3171 - val_loss: 1.3547 - 182ms/epoch - 18ms/step
Epoch 270/300
10/10 - 0s - loss: 1.3216 - val_loss: 1.4041 - 191ms/epoch - 19ms/step
Epoch 271/300
10/10 - 0s - loss: 1.3147 - val_loss: 1.4394 - 182ms/epoch - 18ms/step
Epoch 272/300
10/10 - 0s - loss: 1.3062 - val_loss: 1.4410 - 196ms/epoch - 20ms/step
Epoch 273/300
10/10 - 0s - loss: 1.3154 - val_loss: 1.4076 - 166ms/epoch - 17ms/step
Epoch 274/300
10/10 - 0s - loss: 1.2999 - val_loss: 1.3703 - 161ms/epoch - 16ms/step
Epoch 275/300
10/10 - 0s - loss: 1.2730 - val_loss: 1.3523 - 179ms/epoch - 18ms/step
Epoch 276/300
10/10 - 0s - loss: 1.2773 - val_loss: 1.3488 - 188ms/epoch - 19ms/step
Epoch 277/300
10/10 - 0s - loss: 1.3017 - val_loss: 1.3812 - 184ms/epoch - 18ms/step
Epoch 278/300
10/10 - 0s - loss: 1.2857 - val_loss: 1.4040 - 184ms/epoch - 18ms/step
Epoch 279/300
10/10 - 0s - loss: 1.3243 - val_loss: 1.3774 - 181ms/epoch - 18ms/step
Epoch 280/300
10/10 - 0s - loss: 1.3258 - val_loss: 1.4166 - 161ms/epoch - 16ms/step
Epoch 281/300
10/10 - 0s - loss: 1.3004 - val_loss: 1.3956 - 179ms/epoch - 18ms/step
Epoch 282/300
10/10 - 0s - loss: 1.3407 - val_loss: 1.3529 - 182ms/epoch - 18ms/step
Epoch 283/300
10/10 - 0s - loss: 1.3269 - val_loss: 1.3986 - 183ms/epoch - 18ms/step
Epoch 284/300
10/10 - 0s - loss: 1.3138 - val_loss: 1.4302 - 187ms/epoch - 19ms/step
Epoch 285/300
10/10 - 0s - loss: 1.2999 - val_loss: 1.3942 - 167ms/epoch - 17ms/step
Epoch 286/300
10/10 - 0s - loss: 1.2871 - val_loss: 1.4190 - 161ms/epoch - 16ms/step
Epoch 287/300
10/10 - 0s - loss: 1.3094 - val_loss: 1.3905 - 176ms/epoch - 18ms/step
Epoch 288/300
10/10 - 0s - loss: 1.3072 - val_loss: 1.3681 - 168ms/epoch - 17ms/step
Epoch 289/300
10/10 - 0s - loss: 1.2890 - val_loss: 1.3863 - 190ms/epoch - 19ms/step
Epoch 290/300
10/10 - 0s - loss: 1.2861 - val_loss: 1.4039 - 183ms/epoch - 18ms/step
Epoch 291/300
10/10 - 0s - loss: 1.2845 - val_loss: 1.4018 - 162ms/epoch - 16ms/step
Epoch 292/300
10/10 - 0s - loss: 1.2747 - val_loss: 1.4085 - 184ms/epoch - 18ms/step
Epoch 293/300
10/10 - 0s - loss: 1.2728 - val_loss: 1.3846 - 185ms/epoch - 19ms/step
Epoch 294/300
10/10 - 0s - loss: 1.2567 - val_loss: 1.3465 - 180ms/epoch - 18ms/step
Epoch 295/300
10/10 - 0s - loss: 1.2643 - val_loss: 1.3914 - 195ms/epoch - 20ms/step
Epoch 296/300
10/10 - 0s - loss: 1.2747 - val_loss: 1.4068 - 182ms/epoch - 18ms/step
Epoch 297/300
10/10 - 0s - loss: 1.3311 - val_loss: 1.5587 - 169ms/epoch - 17ms/step
Epoch 298/300
10/10 - 0s - loss: 1.3347 - val_loss: 1.4132 - 181ms/epoch - 18ms/step
Epoch 299/300
10/10 - 0s - loss: 1.3485 - val_loss: 1.4953 - 200ms/epoch - 20ms/step
Epoch 300/300
10/10 - 0s - loss: 1.3156 - val_loss: 1.4378 - 203ms/epoch - 20ms/step
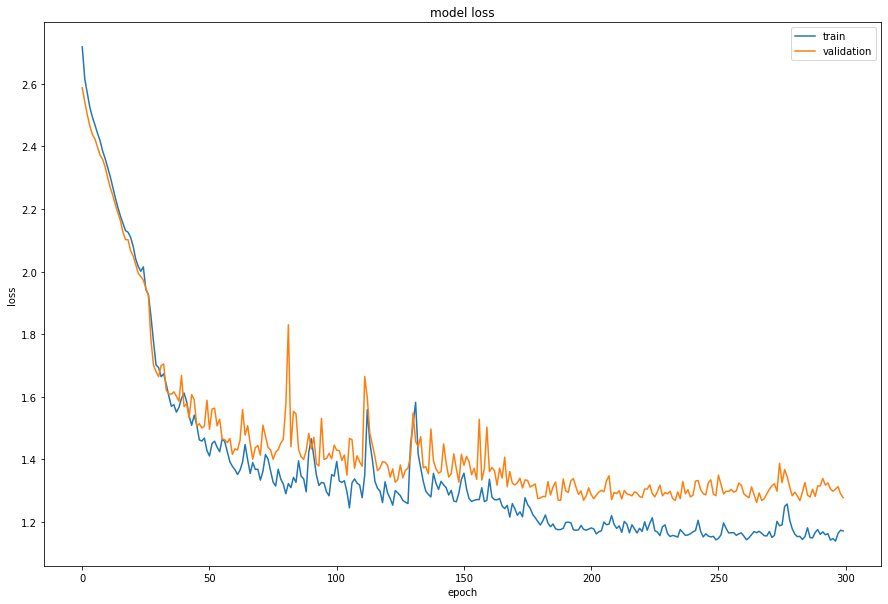
性能评估
plt.figure(figsize=(15, 10))
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.title("模型损失")
plt.legend(["训练", "验证"], loc="upper right")
plt.ylabel("损失")
plt.xlabel("轮次")
# 从数据到潜在空间。
z, _ = model(normalized_data)
# 从潜在空间到数据。
samples = model.distribution.sample(3000)
x, _ = model.predict(samples)
f, axes = plt.subplots(2, 2)
f.set_size_inches(20, 15)
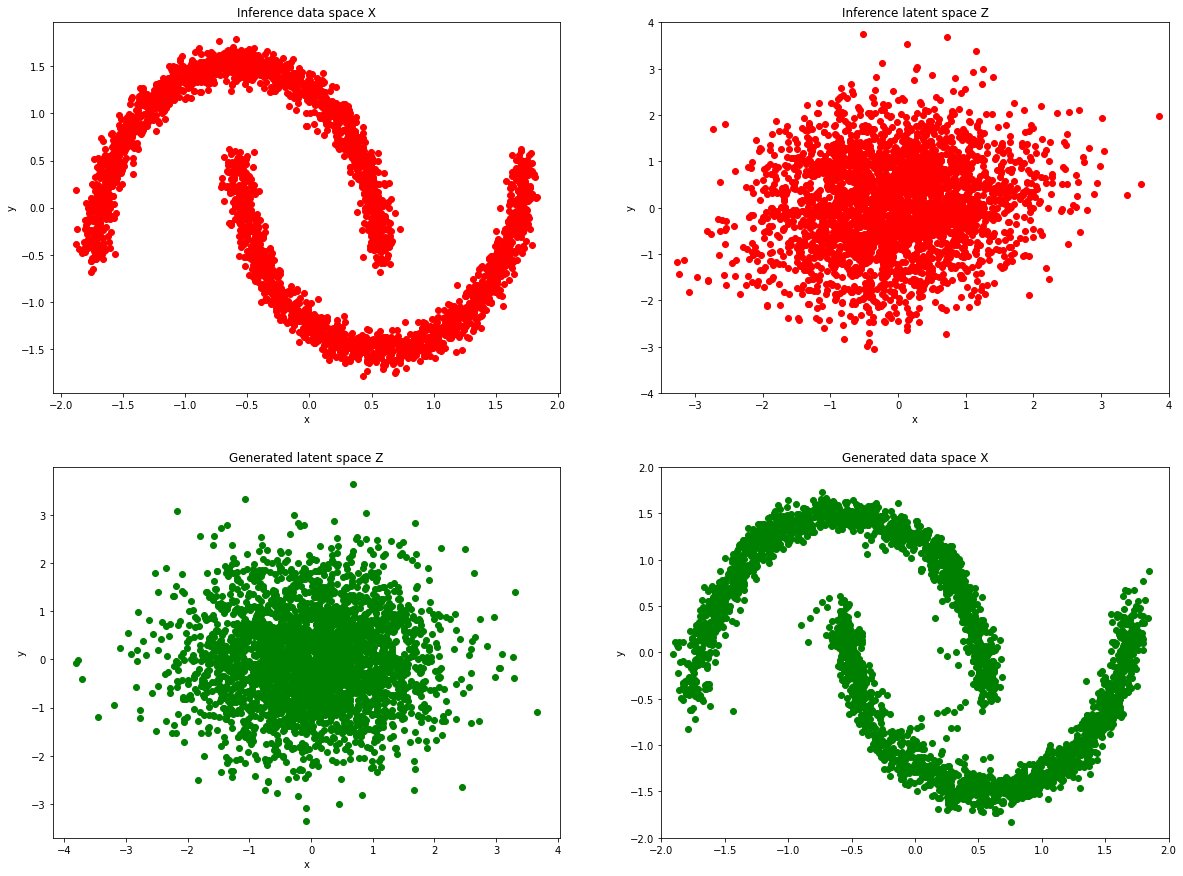
axes[0, 0].scatter(normalized_data[:, 0], normalized_data[:, 1], color="r")
axes[0, 0].set(title="推断数据空间 X", xlabel="x", ylabel="y")
axes[0, 1].scatter(z[:, 0], z[:, 1], color="r")
axes[0, 1].set(title="推断潜在空间 Z", xlabel="x", ylabel="y")
axes[0, 1].set_xlim([-3.5, 4])
axes[0, 1].set_ylim([-4, 4])
axes[1, 0].scatter(samples[:, 0], samples[:, 1], color="g")
axes[1, 0].set(title="生成的潜在空间 Z", xlabel="x", ylabel="y")
axes[1, 1].scatter(x[:, 0], x[:, 1], color="g")
axes[1, 1].set(title="生成的数据空间 X", label="x", ylabel="y")
axes[1, 1].set_xlim([-2, 2])
axes[1, 1].set_ylim([-2, 2])
94/94 [==============================] - 0s 2ms/step
(-2.0, 2.0)