基于图神经网络的节点分类
作者: Khalid Salama
创建日期: 2021/05/30
最后修改: 2021/05/30
描述: 实现一个图神经网络模型,以预测给定引用的论文主题。
介绍
许多机器学习(ML)应用中的数据集在其实体之间存在结构关系,这些关系可以表示为图。这类应用包括社交和通信网络分析、交通预测和欺诈检测。图表示学习旨在构建和训练图数据集模型,以用于各种 ML 任务。
此示例展示了一个简单的 图神经网络 (GNN) 模型的实现。该模型用于在 Cora 数据集 上进行节点预测任务,以根据论文的词和引用网络预测论文的主题。
请注意,我们从头实现一个图卷积层,以提供更好的理解其工作原理。然而,还有许多基于 TensorFlow 的专业库提供丰富的 GNN API,例如 Spectral、StellarGraph 和 GraphNets。
设置
import os
import pandas as pd
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
准备数据集
Cora 数据集由 2,708 篇科学论文组成,这些论文被分类为七个类别之一。引用网络包含 5,429 条链接。每篇论文都有一个大小为 1,433 的二进制词向量,表示相应词的存在。
下载数据集
数据集包含两个制表符分隔的文件:cora.cites 和 cora.content。
cora.cites包含两列的引用记录:cited_paper_id(目标)和citing_paper_id(源)。cora.content包含 1,435 列的论文内容记录:paper_id、subject和 1,433 个二进制特征。
让我们下载数据集。
zip_file = keras.utils.get_file(
fname="cora.tgz",
origin="https://linqs-data.soe.ucsc.edu/public/lbc/cora.tgz",
extract=True,
)
data_dir = os.path.join(os.path.dirname(zip_file), "cora")
处理和可视化数据集
然后,我们将引用数据加载到一个 Pandas DataFrame 中。
citations = pd.read_csv(
os.path.join(data_dir, "cora.cites"),
sep="\t",
header=None,
names=["target", "source"],
)
print("Citations shape:", citations.shape)
Citations shape: (5429, 2)
现在我们显示 citations DataFrame 的一个样本。target 列包含由 source 列中的论文 IDs 引用的论文 IDs。
citations.sample(frac=1).head()
| target | source | |
|---|---|---|
| 2581 | 28227 | 6169 |
| 1500 | 7297 | 7276 |
| 1194 | 6184 | 1105718 |
| 4221 | 139738 | 1108834 |
| 3707 | 79809 | 1153275 |
现在让我们将论文数据加载到一个 Pandas DataFrame 中。
column_names = ["paper_id"] + [f"term_{idx}" for idx in range(1433)] + ["subject"]
papers = pd.read_csv(
os.path.join(data_dir, "cora.content"), sep="\t", header=None, names=column_names,
)
print("Papers shape:", papers.shape)
Papers shape: (2708, 1435)
现在我们显示 papers DataFrame 的一个样本。该 DataFrame 包含 paper_id 和 subject 列,以及表示术语是否存在的 1,433 个二进制列。
in the paper or not.
print(papers.sample(5).T)
1 133 2425 \
paper_id 1061127 34355 1108389
term_0 0 0 0
term_1 0 0 0
term_2 0 0 0
term_3 0 0 0
... ... ... ...
term_1429 0 0 0
term_1430 0 0 0
term_1431 0 0 0
term_1432 0 0 0
subject 规则_学习 神经网络 概率方法
2103 1346
paper_id 1153942 80491
term_0 0 0
term_1 0 0
term_2 1 0
term_3 0 0
... ... ...
term_1429 0 0
term_1430 0 0
term_1431 0 0
term_1432 0 0
subject 遗传算法 神经网络
[1435 rows x 5 columns]
让我们显示每个学科的论文数量。
print(papers.subject.value_counts())
神经网络 818
概率方法 426
遗传算法 418
理论 351
基于案例 298
强化学习 217
规则学习 180
Name: subject, dtype: int64
我们将论文ID和主题转换为零基索引。
class_values = sorted(papers["subject"].unique())
class_idx = {name: id for id, name in enumerate(class_values)}
paper_idx = {name: idx for idx, name in enumerate(sorted(papers["paper_id"].unique()))}
papers["paper_id"] = papers["paper_id"].apply(lambda name: paper_idx[name])
citations["source"] = citations["source"].apply(lambda name: paper_idx[name])
citations["target"] = citations["target"].apply(lambda name: paper_idx[name])
papers["subject"] = papers["subject"].apply(lambda value: class_idx[value])
现在让我们可视化引用图。图中的每个节点代表一篇论文,节点的颜色对应于其主题。请注意,我们仅显示数据集中论文的一个样本。
plt.figure(figsize=(10, 10))
colors = papers["subject"].tolist()
cora_graph = nx.from_pandas_edgelist(citations.sample(n=1500))
subjects = list(papers[papers["paper_id"].isin(list(cora_graph.nodes))]["subject"])
nx.draw_spring(cora_graph, node_size=15, node_color=subjects)

将数据集拆分为按比例分层的训练集和测试集
train_data, test_data = [], []
for _, group_data in papers.groupby("subject"):
# 选择大约50%的数据集用于训练。
random_selection = np.random.rand(len(group_data.index)) <= 0.5
train_data.append(group_data[random_selection])
test_data.append(group_data[~random_selection])
train_data = pd.concat(train_data).sample(frac=1)
test_data = pd.concat(test_data).sample(frac=1)
print("训练数据形状:", train_data.shape)
print("测试数据形状:", test_data.shape)
训练数据形状: (1360, 1435)
测试数据形状: (1348, 1435)
实现训练和评估实验
hidden_units = [32, 32]
learning_rate = 0.01
dropout_rate = 0.5
num_epochs = 300
batch_size = 256
该函数使用给定的训练数据编译并训练输入模型。
def run_experiment(model, x_train, y_train):
# 编译模型。
model.compile(
optimizer=keras.optimizers.Adam(learning_rate),
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=[keras.metrics.SparseCategoricalAccuracy(name="acc")],
)
# 创建一个提前停止的回调。
early_stopping = keras.callbacks.EarlyStopping(
monitor="val_acc", patience=50, restore_best_weights=True
)
# 拟合模型。
history = model.fit(
x=x_train,
y=y_train,
epochs=num_epochs,
batch_size=batch_size,
validation_split=0.15,
callbacks=[early_stopping],
)
return history
该函数显示模型在训练过程中的损失和准确度曲线。
def display_learning_curves(history):
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))
ax1.plot(history.history["loss"])
ax1.plot(history.history["val_loss"])
ax1.legend(["训练", "测试"], loc="upper right")
ax1.set_xlabel("轮数")
ax1.set_ylabel("损失")
ax2.plot(history.history["acc"])
ax2.plot(history.history["val_acc"])
ax2.legend(["训练", "测试"], loc="upper right")
ax2.set_xlabel("轮数")
ax2.set_ylabel("准确率")
plt.show()
实现前馈网络(FFN)模块
我们将在基线和GNN模型中使用该模块。
def create_ffn(hidden_units, dropout_rate, name=None):
fnn_layers = []
for units in hidden_units:
fnn_layers.append(layers.BatchNormalization())
fnn_layers.append(layers.Dropout(dropout_rate))
fnn_layers.append(layers.Dense(units, activation=tf.nn.gelu))
return keras.Sequential(fnn_layers, name=name)
构建基线神经网络模型
为基线模型准备数据
feature_names = list(set(papers.columns) - {"paper_id", "subject"})
num_features = len(feature_names)
num_classes = len(class_idx)
# 创建训练和测试特征作为numpy数组。
x_train = train_data[feature_names].to_numpy()
x_test = test_data[feature_names].to_numpy()
# 创建训练和测试目标作为numpy数组。
y_train = train_data["subject"]
y_test = test_data["subject"]
实现基线分类器
我们添加五个FFN块及跳跃连接,从而生成一个基线模型,其参数数量大致与后面要构建的GNN模型相同。
def create_baseline_model(hidden_units, num_classes, dropout_rate=0.2):
inputs = layers.Input(shape=(num_features,), name="input_features")
x = create_ffn(hidden_units, dropout_rate, name=f"ffn_block1")(inputs)
for block_idx in range(4):
# 创建一个FFN块。
x1 = create_ffn(hidden_units, dropout_rate, name=f"ffn_block{block_idx + 2}")(x)
# 添加跳跃连接。
x = layers.Add(name=f"skip_connection{block_idx + 2}")([x, x1])
# 计算 logits。
logits = layers.Dense(num_classes, name="logits")(x)
# 创建模型。
return keras.Model(inputs=inputs, outputs=logits, name="baseline")
baseline_model = create_baseline_model(hidden_units, num_classes, dropout_rate)
baseline_model.summary()
Model: "baseline"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_features (InputLayer) [(None, 1433)] 0
__________________________________________________________________________________________________
ffn_block1 (Sequential) (None, 32) 52804 input_features[0][0]
__________________________________________________________________________________________________
ffn_block2 (Sequential) (None, 32) 2368 ffn_block1[0][0]
__________________________________________________________________________________________________
skip_connection2 (Add) (None, 32) 0 ffn_block1[0][0]
ffn_block2[0][0]
__________________________________________________________________________________________________
ffn_block3 (Sequential) (None, 32) 2368 skip_connection2[0][0]
__________________________________________________________________________________________________
skip_connection3 (Add) (None, 32) 0 skip_connection2[0][0]
ffn_block3[0][0]
__________________________________________________________________________________________________
ffn_block4 (Sequential) (None, 32) 2368 skip_connection3[0][0]
__________________________________________________________________________________________________
skip_connection4 (Add) (None, 32) 0 skip_connection3[0][0]
ffn_block4[0][0]
__________________________________________________________________________________________________
ffn_block5 (Sequential) (None, 32) 2368 skip_connection4[0][0]
__________________________________________________________________________________________________
skip_connection5 (Add) (None, 32) 0 skip_connection4[0][0]
ffn_block5[0][0]
__________________________________________________________________________________________________
logits (Dense) (None, 7) 231 skip_connection5[0][0]
==================================================================================================
总参数: 62,507
可训练参数: 59,065
不可训练参数: 3,442
__________________________________________________________________________________________________
训练基础分类器
history = run_experiment(baseline_model, x_train, y_train) # 运行实验
Epoch 1/300
5/5 [==============================] - 3s 203ms/step - loss: 4.1695 - acc: 0.1660 - val_loss: 1.9008 - val_acc: 0.3186
Epoch 2/300
5/5 [==============================] - 0s 15ms/step - loss: 2.9269 - acc: 0.2630 - val_loss: 1.8906 - val_acc: 0.3235
Epoch 3/300
5/5 [==============================] - 0s 15ms/step - loss: 2.5669 - acc: 0.2424 - val_loss: 1.8713 - val_acc: 0.3186
Epoch 4/300
5/5 [==============================] - 0s 15ms/step - loss: 2.1377 - acc: 0.3147 - val_loss: 1.8687 - val_acc: 0.3529
Epoch 5/300
5/5 [==============================] - 0s 15ms/step - loss: 2.0256 - acc: 0.3297 - val_loss: 1.8285 - val_acc: 0.3235
Epoch 6/300
5/5 [==============================] - 0s 15ms/step - loss: 1.8148 - acc: 0.3495 - val_loss: 1.8000 - val_acc: 0.3235
Epoch 7/300
5/5 [==============================] - 0s 15ms/step - loss: 1.7216 - acc: 0.3883 - val_loss: 1.7771 - val_acc: 0.3333
Epoch 8/300
5/5 [==============================] - 0s 15ms/step - loss: 1.6941 - acc: 0.3910 - val_loss: 1.7528 - val_acc: 0.3284
Epoch 9/300
5/5 [==============================] - 0s 15ms/step - loss: 1.5690 - acc: 0.4358 - val_loss: 1.7128 - val_acc: 0.3333
Epoch 10/300
5/5 [==============================] - 0s 15ms/step - loss: 1.5139 - acc: 0.4367 - val_loss: 1.6650 - val_acc: 0.3676
Epoch 11/300
5/5 [==============================] - 0s 15ms/step - loss: 1.4370 - acc: 0.4930 - val_loss: 1.6145 - val_acc: 0.3775
Epoch 12/300
5/5 [==============================] - 0s 15ms/step - loss: 1.3696 - acc: 0.5109 - val_loss: 1.5787 - val_acc: 0.3873
Epoch 13/300
5/5 [==============================] - 0s 15ms/step - loss: 1.3979 - acc: 0.5341 - val_loss: 1.5564 - val_acc: 0.3922
Epoch 14/300
5/5 [==============================] - 0s 15ms/step - loss: 1.2681 - acc: 0.5599 - val_loss: 1.5547 - val_acc: 0.3922
Epoch 15/300
5/5 [==============================] - 0s 16ms/step - loss: 1.1970 - acc: 0.5807 - val_loss: 1.5735 - val_acc: 0.3873
Epoch 16/300
5/5 [==============================] - 0s 15ms/step - loss: 1.1555 - acc: 0.6032 - val_loss: 1.5131 - val_acc: 0.4216
Epoch 17/300
5/5 [==============================] - 0s 15ms/step - loss: 1.1234 - acc: 0.6130 - val_loss: 1.4385 - val_acc: 0.4608
Epoch 18/300
5/5 [==============================] - 0s 14ms/step - loss: 1.0507 - acc: 0.6306 - val_loss: 1.3929 - val_acc: 0.4804
Epoch 19/300
5/5 [==============================] - 0s 15ms/step - loss: 1.0341 - acc: 0.6393 - val_loss: 1.3628 - val_acc: 0.4902
Epoch 20/300
5/5 [==============================] - 0s 35ms/step - loss: 0.9457 - acc: 0.6693 - val_loss: 1.3383 - val_acc: 0.4902
Epoch 21/300
5/5 [==============================] - 0s 17ms/step - loss: 0.9054 - acc: 0.6756 - val_loss: 1.3365 - val_acc: 0.4951
Epoch 22/300
5/5 [==============================] - 0s 15ms/step - loss: 0.8952 - acc: 0.6854 - val_loss: 1.3228 - val_acc: 0.5049
Epoch 23/300
5/5 [==============================] - 0s 15ms/step - loss: 0.8413 - acc: 0.7217 - val_loss: 1.2924 - val_acc: 0.5294
Epoch 24/300
5/5 [==============================] - 0s 15ms/step - loss: 0.8543 - acc: 0.6998 - val_loss: 1.2379 - val_acc: 0.5490
Epoch 25/300
5/5 [==============================] - 0s 16ms/step - loss: 0.7632 - acc: 0.7376 - val_loss: 1.1516 - val_acc: 0.5833
Epoch 26/300
5/5 [==============================] - 0s 15ms/step - loss: 0.7189 - acc: 0.7496 - val_loss: 1.1296 - val_acc: 0.5931
Epoch 27/300
5/5 [==============================] - 0s 15ms/step - loss: 0.7433 - acc: 0.7482 - val_loss: 1.0937 - val_acc: 0.6127
Epoch 28/300
5/5 [==============================] - 0s 15ms/step - loss: 0.7310 - acc: 0.7440 - val_loss: 1.0950 - val_acc: 0.5980
Epoch 29/300
5/5 [==============================] - 0s 16ms/step - loss: 0.7059 - acc: 0.7654 - val_loss: 1.1343 - val_acc: 0.5882
Epoch 30/300
5/5 [==============================] - 0s 21ms/step - loss: 0.6831 - acc: 0.7645 - val_loss: 1.1938 - val_acc: 0.5686
Epoch 31/300
5/5 [==============================] - 0s 23ms/step - loss: 0.6741 - acc: 0.7788 - val_loss: 1.1281 - val_acc: 0.5931
Epoch 32/300
5/5 [==============================] - 0s 16ms/step - loss: 0.6344 - acc: 0.7753 - val_loss: 1.0870 - val_acc: 0.6029
Epoch 33/300
5/5 [==============================] - 0s 16ms/step - loss: 0.6052 - acc: 0.7876 - val_loss: 1.0947 - val_acc: 0.6127
Epoch 34/300
5/5 [==============================] - 0s 15ms/step - loss: 0.6313 - acc: 0.7908 - val_loss: 1.1186 - val_acc: 0.5882
Epoch 35/300
5/5 [==============================] - 0s 16ms/step - loss: 0.6163 - acc: 0.7955 - val_loss: 1.0899 - val_acc: 0.6176
Epoch 36/300
5/5 [==============================] - 0s 16ms/step - loss: 0.5388 - acc: 0.8203 - val_loss: 1.1222 - val_acc: 0.5882
Epoch 37/300
5/5 [==============================] - 0s 16ms/step - loss: 0.5487 - acc: 0.8080 - val_loss: 1.0205 - val_acc: 0.6127
Epoch 38/300
5/5 [==============================] - 0s 16ms/step - loss: 0.5885 - acc: 0.7903 - val_loss: 0.9268 - val_acc: 0.6569
Epoch 39/300
5/5 [==============================] - 0s 15ms/step - loss: 0.5541 - acc: 0.8025 - val_loss: 0.9367 - val_acc: 0.6471
Epoch 40/300
5/5 [==============================] - 0s 36ms/step - loss: 0.5594 - acc: 0.7935 - val_loss: 0.9688 - val_acc: 0.6275
Epoch 41/300
5/5 [==============================] - 0s 17ms/step - loss: 0.5255 - acc: 0.8169 - val_loss: 1.0076 - val_acc: 0.6324
Epoch 42/300
5/5 [==============================] - 0s 16ms/step - loss: 0.5284 - acc: 0.8180 - val_loss: 1.0106 - val_acc: 0.6373
Epoch 43/300
5/5 [==============================] - 0s 15ms/step - loss: 0.5141 - acc: 0.8188 - val_loss: 0.8842 - val_acc: 0.6912
Epoch 44/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4767 - acc: 0.8342 - val_loss: 0.8249 - val_acc: 0.7108
Epoch 45/300
5/5 [==============================] - 0s 15ms/step - loss: 0.5915 - acc: 0.8055 - val_loss: 0.8567 - val_acc: 0.6912
Epoch 46/300
5/5 [==============================] - 0s 15ms/step - loss: 0.5026 - acc: 0.8357 - val_loss: 0.9287 - val_acc: 0.6618
Epoch 47/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4859 - acc: 0.8304 - val_loss: 0.9044 - val_acc: 0.6667
Epoch 48/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4860 - acc: 0.8440 - val_loss: 0.8672 - val_acc: 0.6912
Epoch 49/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4723 - acc: 0.8358 - val_loss: 0.8717 - val_acc: 0.6863
Epoch 50/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4831 - acc: 0.8457 - val_loss: 0.8674 - val_acc: 0.6912
Epoch 51/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4873 - acc: 0.8353 - val_loss: 0.8587 - val_acc: 0.7010
Epoch 52/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4537 - acc: 0.8472 - val_loss: 0.8544 - val_acc: 0.7059
Epoch 53/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4684 - acc: 0.8425 - val_loss: 0.8423 - val_acc: 0.7206
Epoch 54/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4436 - acc: 0.8523 - val_loss: 0.8607 - val_acc: 0.6961
Epoch 55/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4589 - acc: 0.8335 - val_loss: 0.8462 - val_acc: 0.7059
Epoch 56/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4757 - acc: 0.8360 - val_loss: 0.8415 - val_acc: 0.7010
Epoch 57/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4270 - acc: 0.8593 - val_loss: 0.8094 - val_acc: 0.7255
Epoch 58/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4530 - acc: 0.8307 - val_loss: 0.8357 - val_acc: 0.7108
Epoch 59/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4370 - acc: 0.8453 - val_loss: 0.8804 - val_acc: 0.7108
Epoch 60/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4379 - acc: 0.8465 - val_loss: 0.8791 - val_acc: 0.7108
Epoch 61/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4254 - acc: 0.8615 - val_loss: 0.8355 - val_acc: 0.7059
Epoch 62/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3929 - acc: 0.8696 - val_loss: 0.8355 - val_acc: 0.7304
Epoch 63/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4039 - acc: 0.8516 - val_loss: 0.8576 - val_acc: 0.7353
Epoch 64/300
5/5 [==============================] - 0s 35ms/step - loss: 0.4220 - acc: 0.8596 - val_loss: 0.8848 - val_acc: 0.7059
Epoch 65/300
5/5 [==============================] - 0s 17ms/step - loss: 0.4091 - acc: 0.8521 - val_loss: 0.8560 - val_acc: 0.7108
Epoch 66/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4658 - acc: 0.8470 - val_loss: 0.8518 - val_acc: 0.7206
Epoch 67/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4269 - acc: 0.8437 - val_loss: 0.7878 - val_acc: 0.7255
Epoch 68/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4368 - acc: 0.8438 - val_loss: 0.7859 - val_acc: 0.7255
Epoch 69/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4113 - acc: 0.8452 - val_loss: 0.8056 - val_acc: 0.7402
Epoch 70/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4304 - acc: 0.8469 - val_loss: 0.8093 - val_acc: 0.7451
Epoch 71/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4159 - acc: 0.8585 - val_loss: 0.8090 - val_acc: 0.7451
Epoch 72/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4218 - acc: 0.8610 - val_loss: 0.8028 - val_acc: 0.7402
Epoch 73/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3632 - acc: 0.8714 - val_loss: 0.8153 - val_acc: 0.7304
Epoch 74/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3745 - acc: 0.8722 - val_loss: 0.8299 - val_acc: 0.7402
Epoch 75/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3997 - acc: 0.8680 - val_loss: 0.8445 - val_acc: 0.7255
Epoch 76/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4143 - acc: 0.8620 - val_loss: 0.8344 - val_acc: 0.7206
Epoch 77/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4006 - acc: 0.8616 - val_loss: 0.8358 - val_acc: 0.7255
Epoch 78/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4266 - acc: 0.8532 - val_loss: 0.8266 - val_acc: 0.7206
Epoch 79/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4337 - acc: 0.8523 - val_loss: 0.8181 - val_acc: 0.7206
Epoch 80/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3857 - acc: 0.8624 - val_loss: 0.8143 - val_acc: 0.7206
Epoch 81/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4146 - acc: 0.8567 - val_loss: 0.8192 - val_acc: 0.7108
Epoch 82/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3638 - acc: 0.8794 - val_loss: 0.8248 - val_acc: 0.7206
Epoch 83/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4126 - acc: 0.8678 - val_loss: 0.8565 - val_acc: 0.7255
Epoch 84/300
5/5 [==============================] - 0s 36ms/step - loss: 0.3941 - acc: 0.8530 - val_loss: 0.8624 - val_acc: 0.7206
Epoch 85/300
5/5 [==============================] - 0s 17ms/step - loss: 0.3843 - acc: 0.8786 - val_loss: 0.8389 - val_acc: 0.7255
Epoch 86/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3651 - acc: 0.8747 - val_loss: 0.8314 - val_acc: 0.7206
Epoch 87/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3911 - acc: 0.8657 - val_loss: 0.8736 - val_acc: 0.7255
Epoch 88/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3706 - acc: 0.8714 - val_loss: 0.9159 - val_acc: 0.7108
Epoch 89/300
5/5 [==============================] - 0s 15ms/step - loss: 0.4403 - acc: 0.8386 - val_loss: 0.9038 - val_acc: 0.7206
Epoch 90/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3865 - acc: 0.8668 - val_loss: 0.8733 - val_acc: 0.7206
Epoch 91/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3757 - acc: 0.8643 - val_loss: 0.8704 - val_acc: 0.7157
Epoch 92/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3828 - acc: 0.8669 - val_loss: 0.8786 - val_acc: 0.7157
Epoch 93/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3651 - acc: 0.8787 - val_loss: 0.8977 - val_acc: 0.7206
Epoch 94/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3913 - acc: 0.8614 - val_loss: 0.9415 - val_acc: 0.7206
Epoch 95/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3995 - acc: 0.8590 - val_loss: 0.9495 - val_acc: 0.7157
Epoch 96/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4228 - acc: 0.8508 - val_loss: 0.9490 - val_acc: 0.7059
Epoch 97/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3853 - acc: 0.8789 - val_loss: 0.9402 - val_acc: 0.7157
Epoch 98/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3711 - acc: 0.8812 - val_loss: 0.9283 - val_acc: 0.7206
Epoch 99/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3949 - acc: 0.8578 - val_loss: 0.9591 - val_acc: 0.7108
Epoch 100/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3563 - acc: 0.8780 - val_loss: 0.9744 - val_acc: 0.7206
Epoch 101/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3579 - acc: 0.8815 - val_loss: 0.9358 - val_acc: 0.7206
Epoch 102/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4069 - acc: 0.8698 - val_loss: 0.9245 - val_acc: 0.7157
Epoch 103/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3161 - acc: 0.8955 - val_loss: 0.9401 - val_acc: 0.7157
Epoch 104/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3346 - acc: 0.8910 - val_loss: 0.9517 - val_acc: 0.7157
Epoch 105/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4204 - acc: 0.8538 - val_loss: 0.9366 - val_acc: 0.7157
Epoch 106/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3492 - acc: 0.8821 - val_loss: 0.9424 - val_acc: 0.7353
Epoch 107/300
5/5 [==============================] - 0s 16ms/step - loss: 0.4002 - acc: 0.8604 - val_loss: 0.9842 - val_acc: 0.7157
Epoch 108/300
5/5 [==============================] - 0s 35ms/step - loss: 0.3701 - acc: 0.8736 - val_loss: 0.9999 - val_acc: 0.7010
Epoch 109/300
5/5 [==============================] - 0s 17ms/step - loss: 0.3391 - acc: 0.8866 - val_loss: 0.9768 - val_acc: 0.6961
Epoch 110/300
5/5 [==============================] - 0s 15ms/step - loss: 0.3857 - acc: 0.8739 - val_loss: 0.9953 - val_acc: 0.7255
Epoch 111/300
5/5 [==============================] - 0s 16ms/step - loss: 0.3822 - acc: 0.8731 - val_loss: 0.9817 - val_acc: 0.7255
Epoch 112/300
5/5 [==============================] - 0s 23ms/step - loss: 0.3211 - acc: 0.8887 - val_loss: 0.9781 - val_acc: 0.7108
Epoch 113/300
5/5 [==============================] - 0s 20ms/step - loss: 0.3473 - acc: 0.8715 - val_loss: 0.9927 - val_acc: 0.6912
Epoch 114/300
5/5 [==============================] - 0s 20ms/step - loss: 0.4026 - acc: 0.8621 - val_loss: 1.0002 - val_acc: 0.6863
Epoch 115/300
5/5 [==============================] - 0s 20ms/step - loss: 0.3413 - acc: 0.8837 - val_loss: 1.0031 - val_acc: 0.6912
Epoch 116/300
5/5 [==============================] - 0s 20ms/step - loss: 0.3653 - acc: 0.8765 - val_loss: 1.0065 - val_acc: 0.7010
Epoch 117/300
5/5 [==============================] - 0s 21ms/step - loss: 0.3147 - acc: 0.8974 - val_loss: 1.0206 - val_acc: 0.7059
Epoch 118/300
5/5 [==============================] - 0s 21ms/step - loss: 0.3639 - acc: 0.8783 - val_loss: 1.0206 - val_acc: 0.7010
Epoch 119/300
5/5 [==============================] - 0s 19ms/step - loss: 0.3660 - acc: 0.8696 - val_loss: 1.0260 - val_acc: 0.6912
Epoch 120/300
5/5 [==============================] - 0s 18ms/step - loss: 0.3624 - acc: 0.8708 - val_loss: 1.0619 - val_acc: 0.6814
让我们绘制学习曲线。
display_learning_curves(history)
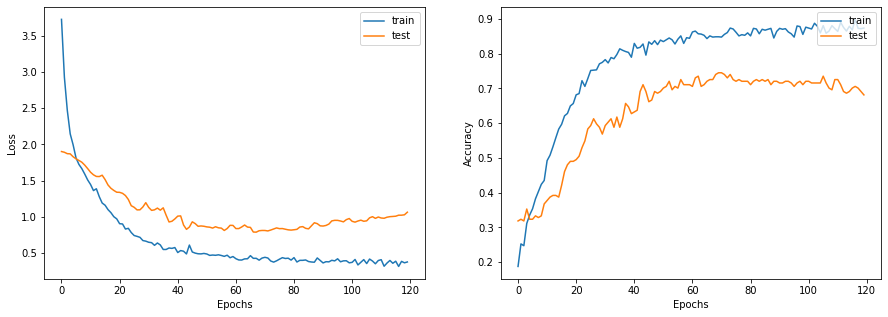
现在我们在测试数据集上评估基线模型。
_, test_accuracy = baseline_model.evaluate(x=x_test, y=y_test, verbose=0)
print(f"测试准确率: {round(test_accuracy * 100, 2)}%")
测试准确率: 73.52%
检查基线模型预测
让我们通过随机生成关于单词出现概率的二元词向量来创建新的数据实例。
def generate_random_instances(num_instances):
token_probability = x_train.mean(axis=0)
instances = []
for _ in range(num_instances):
probabilities = np.random.uniform(size=len(token_probability))
instance = (probabilities <= token_probability).astype(int)
instances.append(instance)
return np.array(instances)
def display_class_probabilities(probabilities):
for instance_idx, probs in enumerate(probabilities):
print(f"实例 {instance_idx + 1}:")
for class_idx, prob in enumerate(probs):
print(f"- {class_values[class_idx]}: {round(prob * 100, 2)}%")
现在,我们展示基线模型在这些随机生成实例上的预测结果。
new_instances = generate_random_instances(num_classes)
logits = baseline_model.predict(new_instances)
probabilities = keras.activations.softmax(tf.convert_to_tensor(logits)).numpy()
display_class_probabilities(probabilities)
实例 1:
- Case_Based: 13.02%
- Genetic_Algorithms: 6.89%
- Neural_Networks: 23.32%
- Probabilistic_Methods: 47.89%
- Reinforcement_Learning: 2.66%
- Rule_Learning: 1.18%
- Theory: 5.03%
实例 2:
- Case_Based: 1.64%
- Genetic_Algorithms: 59.74%
- Neural_Networks: 27.13%
- Probabilistic_Methods: 9.02%
- Reinforcement_Learning: 1.05%
- Rule_Learning: 0.12%
- Theory: 1.31%
实例 3:
- Case_Based: 1.35%
- Genetic_Algorithms: 77.41%
- Neural_Networks: 9.56%
- Probabilistic_Methods: 7.89%
- Reinforcement_Learning: 0.42%
- Rule_Learning: 0.46%
- Theory: 2.92%
实例 4:
- Case_Based: 0.43%
- Genetic_Algorithms: 3.87%
- Neural_Networks: 92.88%
- Probabilistic_Methods: 0.97%
- Reinforcement_Learning: 0.56%
- Rule_Learning: 0.09%
- Theory: 1.2%
实例 5:
- Case_Based: 0.11%
- Genetic_Algorithms: 0.17%
- Neural_Networks: 10.26%
- Probabilistic_Methods: 0.5%
- Reinforcement_Learning: 0.35%
- Rule_Learning: 0.63%
- Theory: 87.97%
实例 6:
- Case_Based: 0.98%
- Genetic_Algorithms: 23.37%
- Neural_Networks: 70.76%
- Probabilistic_Methods: 1.12%
- Reinforcement_Learning: 2.23%
- Rule_Learning: 0.21%
- Theory: 1.33%
实例 7:
- Case_Based: 0.64%
- Genetic_Algorithms: 2.42%
- Neural_Networks: 27.19%
- Probabilistic_Methods: 14.07%
- Reinforcement_Learning: 1.62%
- Rule_Learning: 9.35%
- Theory: 44.7%
构建图神经网络模型
准备图模型的数据
准备和加载图数据到模型中进行训练是在GNN模型中最具挑战性的部分,这一部分在不同的专用库中以不同的方式进行处理。在这个例子中,我们展示了一种简单的方法来准备和使用图数据,如果你的数据集由完全能够放入内存的单个图组成,这种方法是合适的。
图数据由 graph_info 元组表示,包含以下三个元素:
node_features: 这是一个形状为[num_nodes, num_features]的 NumPy 数组,包含节点特征。在这个数据集中,节点是论文,而node_features是每篇论文的单词存在二元向量。edges: 这是一个形状为[num_edges, num_edges]的 NumPy 数组,表示节点之间链接的稀疏 邻接矩阵。在这个示例中,链接是论文之间的引用关系。edge_weights(可选):这是一个形状为[num_edges]的 NumPy 数组,包含边的权重,量化 图中节点之间的关系。在这个示例中,论文引用没有权重。
# 创建一个形状为 [2, num_edges] 的边数组(稀疏邻接矩阵)。
edges = citations[["source", "target"]].to_numpy().T
# 创建一个全为1的边权重数组。
edge_weights = tf.ones(shape=edges.shape[1])
# 创建一个形状为 [num_nodes, num_features] 的节点特征数组。
node_features = tf.cast(
papers.sort_values("paper_id")[feature_names].to_numpy(), dtype=tf.dtypes.float32
)
# 创建包含节点特征、边和边权重的图信息元组。
graph_info = (node_features, edges, edge_weights)
print("边的形状:", edges.shape)
print("节点的形状:", node_features.shape)
边的形状: (2, 5429)
节点的形状: (2708, 1433)
实现图卷积层
我们将图卷积模块实现为一个 Keras 层。我们的 GraphConvLayer 执行以下步骤:
- 准备:输入节点表示通过 FFN 处理以生成一个 信息。您可以通过只应用线性变换来简化处理。
- 聚合:每个节点邻居的信息与
edge_weights使用 置换不变 的池化操作(如 sum、mean 和 max)进行聚合,以准备每个节点的单一聚合信息。例如,参见 tf.math.unsorted_segment_sum APIs 用于聚合邻居信息。 - 更新:
node_repesentations和aggregated_messages的形状均为[num_nodes, representation_dim],二者结合并处理以生成节点表示(节点嵌入)的新状态。如果combination_type为gru,则node_repesentations和aggregated_messages被堆叠以创建序列,然后由 GRU 层处理。否则,node_repesentations和aggregated_messages被相加或连接,然后使用 FFN 处理。
实施的技术借鉴了 图卷积网络、GraphSage、图同构网络、简单图网络 和 门控图序列神经网络 的思想。还有其他两个关键技术未涉及:图注意力网络 和 消息传递神经网络。
def create_gru(hidden_units, dropout_rate):
inputs = keras.layers.Input(shape=(2, hidden_units[0]))
x = inputs
for units in hidden_units:
x = layers.GRU(
units=units,
activation="tanh",
recurrent_activation="sigmoid",
return_sequences=True,
dropout=dropout_rate,
return_state=False,
recurrent_dropout=dropout_rate,
)(x)
return keras.Model(inputs=inputs, outputs=x)
class GraphConvLayer(layers.Layer):
def __init__(
self,
hidden_units,
dropout_rate=0.2,
aggregation_type="mean",
combination_type="concat",
normalize=False,
*args,
**kwargs,
):
super().__init__(*args, **kwargs)
self.aggregation_type = aggregation_type
self.combination_type = combination_type
self.normalize = normalize
self.ffn_prepare = create_ffn(hidden_units, dropout_rate)
if self.combination_type == "gru":
self.update_fn = create_gru(hidden_units, dropout_rate)
else:
self.update_fn = create_ffn(hidden_units, dropout_rate)
def prepare(self, node_repesentations, weights=None):
# node_repesentations 的形状是 [num_edges, embedding_dim].
messages = self.ffn_prepare(node_repesentations)
if weights is not None:
messages = messages * tf.expand_dims(weights, -1)
return messages
def aggregate(self, node_indices, neighbour_messages, node_repesentations):
# node_indices 的形状是 [num_edges].
# neighbour_messages 的形状: [num_edges, representation_dim].
# node_repesentations 的形状是 [num_nodes, representation_dim]
num_nodes = node_repesentations.shape[0]
if self.aggregation_type == "sum":
aggregated_message = tf.math.unsorted_segment_sum(
neighbour_messages, node_indices, num_segments=num_nodes
)
elif self.aggregation_type == "mean":
aggregated_message = tf.math.unsorted_segment_mean(
neighbour_messages, node_indices, num_segments=num_nodes
)
elif self.aggregation_type == "max":
aggregated_message = tf.math.unsorted_segment_max(
neighbour_messages, node_indices, num_segments=num_nodes
)
else:
raise ValueError(f"无效的聚合类型: {self.aggregation_type}.")
return aggregated_message
def update(self, node_repesentations, aggregated_messages):
# node_repesentations 的形状是 [num_nodes, representation_dim].
# aggregated_messages 的形状是 [num_nodes, representation_dim].
if self.combination_type == "gru":
# 为 GRU 层创建两个元素的序列。
h = tf.stack([node_repesentations, aggregated_messages], axis=1)
elif self.combination_type == "concat":
# 连接 node_repesentations 和 aggregated_messages.
h = tf.concat([node_repesentations, aggregated_messages], axis=1)
elif self.combination_type == "add":
# 加法 node_repesentations 和 aggregated_messages.
h = node_repesentations + aggregated_messages
else:
raise ValueError(f"无效的组合类型: {self.combination_type}.")
# 应用处理函数。
node_embeddings = self.update_fn(h)
if self.combination_type == "gru":
node_embeddings = tf.unstack(node_embeddings, axis=1)[-1]
if self.normalize:
node_embeddings = tf.nn.l2_normalize(node_embeddings, axis=-1)
return node_embeddings
def call(self, inputs):
"""处理输入以生成 node_embeddings.
inputs: 包含三个元素的元组: node_repesentations, edges, edge_weights.
返回: 形状为 [num_nodes, representation_dim] 的 node_embeddings.
"""
node_repesentations, edges, edge_weights = inputs
# 从边缘获取 node_indices (源) 和 neighbour_indices (目标).
node_indices, neighbour_indices = edges[0], edges[1]
# neighbour_repesentations 的形状是 [num_edges, representation_dim].
neighbour_repesentations = tf.gather(node_repesentations, neighbour_indices)
# 准备邻居的消息.
neighbour_messages = self.prepare(neighbour_repesentations, edge_weights)
# 聚合邻居消息.
aggregated_messages = self.aggregate(
node_indices, neighbour_messages, node_repesentations
)
# 使用邻居消息更新节点嵌入.
return self.update(node_repesentations, aggregated_messages)
实现图神经网络节点分类器
GNN分类模型遵循图神经网络的设计空间的方法,步骤如下:
- 使用FFN对节点特征进行预处理,以生成初始节点表示。
- 对节点表示应用一个或多个图卷积层,带有跳跃连接,生成节点嵌入。
- 使用FFN对节点嵌入进行后处理,以生成最终节点嵌入。
- 将节点嵌入在Softmax层中输入,以预测节点类别。
每个添加的图卷积层捕获来自更远邻居的信息。然而,添加多个图卷积层可能会导致过平滑,模型为所有节点生成相似的嵌入。
请注意,传递给Keras模型构造函数的graph_info,并作为Keras模型对象的属性使用,而不是训练或预测的输入数据。模型将接受一批node_indices,用于从graph_info中查找节点特征和邻居。
class GNNNodeClassifier(tf.keras.Model):
def __init__(
self,
graph_info,
num_classes,
hidden_units,
aggregation_type="sum",
combination_type="concat",
dropout_rate=0.2,
normalize=True,
*args,
**kwargs,
):
super().__init__(*args, **kwargs)
# 解包graph_info为三个元素:节点特征,边和边权重。
node_features, edges, edge_weights = graph_info
self.node_features = node_features
self.edges = edges
self.edge_weights = edge_weights
# 如果未提供,则将edge_weights设置为1。
if self.edge_weights is None:
self.edge_weights = tf.ones(shape=edges.shape[1])
# 将edge_weights的总和归一化为1。
self.edge_weights = self.edge_weights / tf.math.reduce_sum(self.edge_weights)
# 创建一个处理层。
self.preprocess = create_ffn(hidden_units, dropout_rate, name="preprocess")
# 创建第一个GraphConv层。
self.conv1 = GraphConvLayer(
hidden_units,
dropout_rate,
aggregation_type,
combination_type,
normalize,
name="graph_conv1",
)
# 创建第二个GraphConv层。
self.conv2 = GraphConvLayer(
hidden_units,
dropout_rate,
aggregation_type,
combination_type,
normalize,
name="graph_conv2",
)
# 创建一个后处理层。
self.postprocess = create_ffn(hidden_units, dropout_rate, name="postprocess")
# 创建一个计算logits层。
self.compute_logits = layers.Dense(units=num_classes, name="logits")
def call(self, input_node_indices):
# 对node_features进行预处理以生成节点表示。
x = self.preprocess(self.node_features)
# 应用第一个图卷积层。
x1 = self.conv1((x, self.edges, self.edge_weights))
# 跳跃连接。
x = x1 + x
# 应用第二个图卷积层。
x2 = self.conv2((x, self.edges, self.edge_weights))
# 跳跃连接。
x = x2 + x
# 对节点嵌入进行后处理。
x = self.postprocess(x)
# 为输入的node_indices获取节点嵌入。
node_embeddings = tf.gather(x, input_node_indices)
# 计算logits
return self.compute_logits(node_embeddings)
让我们测试实例化和调用GNN模型。注意,如果提供N个节点索引,输出将是形状为[N, num_classes]的张量,与图的大小无关。
gnn_model = GNNNodeClassifier(
graph_info=graph_info,
num_classes=num_classes,
hidden_units=hidden_units,
dropout_rate=dropout_rate,
name="gnn_model",
)
print("GNN输出形状:", gnn_model([1, 10, 100]))
gnn_model.summary()
GNN 输出形状: tf.Tensor( [[ 0.00620723 0.06162593 0.0176599 0.00830251 -0.03019211 -0.00402163 0.00277454] [ 0.01705155 -0.0467547 0.01400987 -0.02146192 -0.11757397 0.10820404 -0.0375765 ] [-0.02516522 -0.05514468 -0.03842098 -0.0495692 -0.05128997 -0.02241635 -0.07738923]], shape=(3, 7), dtype=float32) 模型: "gnn_model"
层 (类型) 输出形状 参数 #
预处理 (序列) (2708, 32) 52804
图卷积层1 (GraphConvLayer) 多个 5888
图卷积层2 (GraphConvLayer) 多个 5888
后处理 (序列) (2708, 32) 2368
逻辑层 (Dense) 多个 231
总参数: 67,179 可训练参数: 63,481 不可训练参数: 3,698
训练GNN模型
请注意,我们使用标准的监督交叉熵损失来训练模型。 然而,我们可以为生成的节点嵌入添加另一个自监督损失项,以确保图中的相邻节点具有相似的表示,而远离的节点具有不相似的表示。
x_train = train_data.paper_id.to_numpy()
history = run_experiment(gnn_model, x_train, y_train)
Epoch 1/300
5/5 [==============================] - 4s 188ms/step - loss: 2.2529 - acc: 0.1793 - val_loss: 1.8933 - val_acc: 0.2941
Epoch 2/300
5/5 [==============================] - 0s 83ms/step - loss: 1.9866 - acc: 0.2601 - val_loss: 1.8753 - val_acc: 0.3186
Epoch 3/300
5/5 [==============================] - 0s 77ms/step - loss: 1.8794 - acc: 0.2846 - val_loss: 1.8655 - val_acc: 0.3186
Epoch 4/300
5/5 [==============================] - 0s 74ms/step - loss: 1.8432 - acc: 0.3078 - val_loss: 1.8529 - val_acc: 0.3186
Epoch 5/300
5/5 [==============================] - 0s 69ms/step - loss: 1.8314 - acc: 0.3134 - val_loss: 1.8429 - val_acc: 0.3186
Epoch 6/300
5/5 [==============================] - 0s 68ms/step - loss: 1.8157 - acc: 0.3208 - val_loss: 1.8326 - val_acc: 0.3186
Epoch 7/300
5/5 [==============================] - 0s 94ms/step - loss: 1.8112 - acc: 0.3071 - val_loss: 1.8265 - val_acc: 0.3186
Epoch 8/300
5/5 [==============================] - 0s 67ms/step - loss: 1.8028 - acc: 0.3132 - val_loss: 1.8171 - val_acc: 0.3186
Epoch 9/300
5/5 [==============================] - 0s 68ms/step - loss: 1.8007 - acc: 0.3206 - val_loss: 1.7961 - val_acc: 0.3186
Epoch 10/300
5/5 [==============================] - 0s 68ms/step - loss: 1.7571 - acc: 0.3259 - val_loss: 1.7623 - val_acc: 0.3186
Epoch 11/300
5/5 [==============================] - 0s 68ms/step - loss: 1.7373 - acc: 0.3279 - val_loss: 1.7131 - val_acc: 0.3186
Epoch 12/300
5/5 [==============================] - 0s 76ms/step - loss: 1.7130 - acc: 0.3169 - val_loss: 1.6552 - val_acc: 0.3186
Epoch 13/300
5/5 [==============================] - 0s 70ms/step - loss: 1.6989 - acc: 0.3315 - val_loss: 1.6075 - val_acc: 0.3284
Epoch 14/300
5/5 [==============================] - 0s 79ms/step - loss: 1.6733 - acc: 0.3522 - val_loss: 1.6027 - val_acc: 0.3333
Epoch 15/300
5/5 [==============================] - 0s 75ms/step - loss: 1.6060 - acc: 0.3641 - val_loss: 1.6422 - val_acc: 0.3480
Epoch 16/300
5/5 [==============================] - 0s 68ms/step - loss: 1.5783 - acc: 0.3924 - val_loss: 1.6893 - val_acc: 0.3676
Epoch 17/300
5/5 [==============================] - 0s 70ms/step - loss: 1.5269 - acc: 0.4315 - val_loss: 1.7534 - val_acc: 0.3725
Epoch 18/300
5/5 [==============================] - 0s 77ms/step - loss: 1.4558 - acc: 0.4633 - val_loss: 1.7224 - val_acc: 0.4167
Epoch 19/300
5/5 [==============================] - 0s 75ms/step - loss: 1.4131 - acc: 0.4765 - val_loss: 1.6482 - val_acc: 0.4510
Epoch 20/300
5/5 [==============================] - 0s 70ms/step - loss: 1.3880 - acc: 0.4859 - val_loss: 1.4956 - val_acc: 0.4706
Epoch 21/300
5/5 [==============================] - 0s 73ms/step - loss: 1.3223 - acc: 0.5166 - val_loss: 1.5299 - val_acc: 0.4853
Epoch 22/300
5/5 [==============================] - 0s 75ms/step - loss: 1.3226 - acc: 0.5172 - val_loss: 1.6304 - val_acc: 0.4902
Epoch 23/300
5/5 [==============================] - 0s 75ms/step - loss: 1.2888 - acc: 0.5267 - val_loss: 1.6679 - val_acc: 0.5000
Epoch 24/300
5/5 [==============================] - 0s 69ms/step - loss: 1.2478 - acc: 0.5279 - val_loss: 1.6552 - val_acc: 0.4853
Epoch 25/300
5/5 [==============================] - 0s 70ms/step - loss: 1.1978 - acc: 0.5720 - val_loss: 1.6705 - val_acc: 0.4902
Epoch 26/300
5/5 [==============================] - 0s 70ms/step - loss: 1.1814 - acc: 0.5596 - val_loss: 1.6327 - val_acc: 0.5343
Epoch 27/300
5/5 [==============================] - 0s 68ms/step - loss: 1.1085 - acc: 0.5979 - val_loss: 1.5184 - val_acc: 0.5245
Epoch 28/300
5/5 [==============================] - 0s 69ms/step - loss: 1.0695 - acc: 0.6078 - val_loss: 1.5212 - val_acc: 0.4853
Epoch 29/300
5/5 [==============================] - 0s 70ms/step - loss: 1.1063 - acc: 0.6002 - val_loss: 1.5988 - val_acc: 0.4706
Epoch 30/300
5/5 [==============================] - 0s 68ms/step - loss: 1.0194 - acc: 0.6326 - val_loss: 1.5636 - val_acc: 0.4951
Epoch 31/300
5/5 [==============================] - 0s 70ms/step - loss: 1.0320 - acc: 0.6268 - val_loss: 1.5191 - val_acc: 0.5196
Epoch 32/300
5/5 [==============================] - 0s 82ms/step - loss: 0.9749 - acc: 0.6433 - val_loss: 1.5922 - val_acc: 0.5098
Epoch 33/300
5/5 [==============================] - 0s 85ms/step - loss: 0.9095 - acc: 0.6717 - val_loss: 1.5879 - val_acc: 0.5000
Epoch 34/300
5/5 [==============================] - 0s 78ms/step - loss: 0.9324 - acc: 0.6903 - val_loss: 1.5717 - val_acc: 0.4951
Epoch 35/300
5/5 [==============================] - 0s 80ms/step - loss: 0.8908 - acc: 0.6953 - val_loss: 1.5010 - val_acc: 0.5098
Epoch 36/300
5/5 [==============================] - 0s 99ms/step - loss: 0.8858 - acc: 0.6977 - val_loss: 1.5939 - val_acc: 0.5147
Epoch 37/300
5/5 [==============================] - 0s 79ms/step - loss: 0.8376 - acc: 0.6991 - val_loss: 1.4000 - val_acc: 0.5833
Epoch 38/300
5/5 [==============================] - 0s 75ms/step - loss: 0.8657 - acc: 0.7080 - val_loss: 1.3288 - val_acc: 0.5931
Epoch 39/300
5/5 [==============================] - 0s 86ms/step - loss: 0.9160 - acc: 0.6819 - val_loss: 1.1358 - val_acc: 0.6275
Epoch 40/300
5/5 [==============================] - 0s 80ms/step - loss: 0.8676 - acc: 0.7109 - val_loss: 1.0618 - val_acc: 0.6765
Epoch 41/300
5/5 [==============================] - 0s 72ms/step - loss: 0.8065 - acc: 0.7246 - val_loss: 1.0785 - val_acc: 0.6765
Epoch 42/300
5/5 [==============================] - 0s 76ms/step - loss: 0.8478 - acc: 0.7145 - val_loss: 1.0502 - val_acc: 0.6569
Epoch 43/300
5/5 [==============================] - 0s 78ms/step - loss: 0.8125 - acc: 0.7068 - val_loss: 0.9888 - val_acc: 0.6520
Epoch 44/300
5/5 [==============================] - 0s 68ms/step - loss: 0.7791 - acc: 0.7425 - val_loss: 0.9820 - val_acc: 0.6618
Epoch 45/300
5/5 [==============================] - 0s 69ms/step - loss: 0.7492 - acc: 0.7368 - val_loss: 0.9297 - val_acc: 0.6961
Epoch 46/300
5/5 [==============================] - 0s 71ms/step - loss: 0.7521 - acc: 0.7668 - val_loss: 0.9757 - val_acc: 0.6961
Epoch 47/300
5/5 [==============================] - 0s 71ms/step - loss: 0.7090 - acc: 0.7587 - val_loss: 0.9676 - val_acc: 0.7059
Epoch 48/300
5/5 [==============================] - 0s 68ms/step - loss: 0.7008 - acc: 0.7430 - val_loss: 0.9457 - val_acc: 0.7010
Epoch 49/300
5/5 [==============================] - 0s 69ms/step - loss: 0.6919 - acc: 0.7584 - val_loss: 0.9998 - val_acc: 0.6569
Epoch 50/300
5/5 [==============================] - 0s 68ms/step - loss: 0.7583 - acc: 0.7628 - val_loss: 0.9707 - val_acc: 0.6667
Epoch 51/300
5/5 [==============================] - 0s 69ms/step - loss: 0.6575 - acc: 0.7697 - val_loss: 0.9260 - val_acc: 0.6814
Epoch 52/300
5/5 [==============================] - 0s 78ms/step - loss: 0.6751 - acc: 0.7774 - val_loss: 0.9173 - val_acc: 0.6765
Epoch 53/300
5/5 [==============================] - 0s 92ms/step - loss: 0.6964 - acc: 0.7561 - val_loss: 0.8985 - val_acc: 0.6961
Epoch 54/300
5/5 [==============================] - 0s 77ms/step - loss: 0.6386 - acc: 0.7872 - val_loss: 0.9455 - val_acc: 0.6961
Epoch 55/300
5/5 [==============================] - 0s 77ms/step - loss: 0.6110 - acc: 0.8130 - val_loss: 0.9780 - val_acc: 0.6716
Epoch 56/300
5/5 [==============================] - 0s 76ms/step - loss: 0.6483 - acc: 0.7703 - val_loss: 0.9650 - val_acc: 0.6863
Epoch 57/300
5/5 [==============================] - 0s 78ms/step - loss: 0.6811 - acc: 0.7706 - val_loss: 0.9446 - val_acc: 0.6667
Epoch 58/300
5/5 [==============================] - 0s 76ms/step - loss: 0.6391 - acc: 0.7852 - val_loss: 0.9059 - val_acc: 0.7010
Epoch 59/300
5/5 [==============================] - 0s 76ms/step - loss: 0.6533 - acc: 0.7784 - val_loss: 0.8964 - val_acc: 0.7108
Epoch 60/300
5/5 [==============================] - 0s 101ms/step - loss: 0.6587 - acc: 0.7863 - val_loss: 0.8417 - val_acc: 0.7108
Epoch 61/300
5/5 [==============================] - 0s 84ms/step - loss: 0.5776 - acc: 0.8166 - val_loss: 0.8035 - val_acc: 0.7304
Epoch 62/300
5/5 [==============================] - 0s 80ms/step - loss: 0.6396 - acc: 0.7792 - val_loss: 0.8072 - val_acc: 0.7500
Epoch 63/300
5/5 [==============================] - 0s 67ms/step - loss: 0.6201 - acc: 0.7972 - val_loss: 0.7809 - val_acc: 0.7696
Epoch 64/300
5/5 [==============================] - 0s 68ms/step - loss: 0.6358 - acc: 0.7875 - val_loss: 0.7635 - val_acc: 0.7500
Epoch 65/300
5/5 [==============================] - 0s 70ms/step - loss: 0.5914 - acc: 0.8027 - val_loss: 0.8147 - val_acc: 0.7402
Epoch 66/300
5/5 [==============================] - 0s 69ms/step - loss: 0.5960 - acc: 0.7955 - val_loss: 0.9350 - val_acc: 0.7304
Epoch 67/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5752 - acc: 0.8001 - val_loss: 0.9849 - val_acc: 0.7157
Epoch 68/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5189 - acc: 0.8322 - val_loss: 1.0268 - val_acc: 0.7206
Epoch 69/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5413 - acc: 0.8078 - val_loss: 0.9132 - val_acc: 0.7549
Epoch 70/300
5/5 [==============================] - 0s 75ms/step - loss: 0.5231 - acc: 0.8222 - val_loss: 0.8673 - val_acc: 0.7647
Epoch 71/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5416 - acc: 0.8219 - val_loss: 0.8179 - val_acc: 0.7696
Epoch 72/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5060 - acc: 0.8263 - val_loss: 0.7870 - val_acc: 0.7794
Epoch 73/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5502 - acc: 0.8221 - val_loss: 0.7749 - val_acc: 0.7549
Epoch 74/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5111 - acc: 0.8434 - val_loss: 0.7830 - val_acc: 0.7549
Epoch 75/300
5/5 [==============================] - 0s 69ms/step - loss: 0.5119 - acc: 0.8386 - val_loss: 0.8140 - val_acc: 0.7451
Epoch 76/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4922 - acc: 0.8433 - val_loss: 0.8149 - val_acc: 0.7353
Epoch 77/300
5/5 [==============================] - 0s 71ms/step - loss: 0.5217 - acc: 0.8188 - val_loss: 0.7784 - val_acc: 0.7598
Epoch 78/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5027 - acc: 0.8410 - val_loss: 0.7660 - val_acc: 0.7696
Epoch 79/300
5/5 [==============================] - 0s 67ms/step - loss: 0.5307 - acc: 0.8265 - val_loss: 0.7217 - val_acc: 0.7696
Epoch 80/300
5/5 [==============================] - 0s 68ms/step - loss: 0.5164 - acc: 0.8239 - val_loss: 0.6974 - val_acc: 0.7647
Epoch 81/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4404 - acc: 0.8526 - val_loss: 0.6891 - val_acc: 0.7745
Epoch 82/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4565 - acc: 0.8449 - val_loss: 0.6839 - val_acc: 0.7696
Epoch 83/300
5/5 [==============================] - 0s 67ms/step - loss: 0.4759 - acc: 0.8491 - val_loss: 0.7162 - val_acc: 0.7745
Epoch 84/300
5/5 [==============================] - 0s 70ms/step - loss: 0.5154 - acc: 0.8476 - val_loss: 0.7889 - val_acc: 0.7598
Epoch 85/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4847 - acc: 0.8480 - val_loss: 0.7579 - val_acc: 0.7794
Epoch 86/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4519 - acc: 0.8592 - val_loss: 0.7056 - val_acc: 0.7941
Epoch 87/300
5/5 [==============================] - 0s 67ms/step - loss: 0.5038 - acc: 0.8472 - val_loss: 0.6725 - val_acc: 0.7794
Epoch 88/300
5/5 [==============================] - 0s 92ms/step - loss: 0.4729 - acc: 0.8454 - val_loss: 0.7057 - val_acc: 0.7745
Epoch 89/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4811 - acc: 0.8562 - val_loss: 0.6784 - val_acc: 0.7990
Epoch 90/300
5/5 [==============================] - 0s 70ms/step - loss: 0.4102 - acc: 0.8779 - val_loss: 0.6383 - val_acc: 0.8039
Epoch 91/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4493 - acc: 0.8703 - val_loss: 0.6574 - val_acc: 0.7941
Epoch 92/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4560 - acc: 0.8610 - val_loss: 0.6764 - val_acc: 0.7941
Epoch 93/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4465 - acc: 0.8626 - val_loss: 0.6628 - val_acc: 0.7892
Epoch 94/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4773 - acc: 0.8446 - val_loss: 0.6573 - val_acc: 0.7941
Epoch 95/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4313 - acc: 0.8734 - val_loss: 0.6875 - val_acc: 0.7941
Epoch 96/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4668 - acc: 0.8598 - val_loss: 0.6712 - val_acc: 0.8039
Epoch 97/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4329 - acc: 0.8696 - val_loss: 0.6274 - val_acc: 0.8088
Epoch 98/300
5/5 [==============================] - 0s 71ms/step - loss: 0.4223 - acc: 0.8542 - val_loss: 0.6259 - val_acc: 0.7990
Epoch 99/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4677 - acc: 0.8488 - val_loss: 0.6431 - val_acc: 0.8186
Epoch 100/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3933 - acc: 0.8753 - val_loss: 0.6559 - val_acc: 0.8186
Epoch 101/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3945 - acc: 0.8777 - val_loss: 0.6461 - val_acc: 0.8186
Epoch 102/300
5/5 [==============================] - 0s 70ms/step - loss: 0.4671 - acc: 0.8324 - val_loss: 0.6607 - val_acc: 0.7990
Epoch 103/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3890 - acc: 0.8762 - val_loss: 0.6792 - val_acc: 0.7941
Epoch 104/300
5/5 [==============================] - 0s 67ms/step - loss: 0.4336 - acc: 0.8646 - val_loss: 0.6854 - val_acc: 0.7990
Epoch 105/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4304 - acc: 0.8651 - val_loss: 0.6949 - val_acc: 0.8039
Epoch 106/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4043 - acc: 0.8723 - val_loss: 0.6941 - val_acc: 0.7892
Epoch 107/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4043 - acc: 0.8713 - val_loss: 0.6798 - val_acc: 0.8088
Epoch 108/300
5/5 [==============================] - 0s 70ms/step - loss: 0.4647 - acc: 0.8599 - val_loss: 0.6726 - val_acc: 0.8039
Epoch 109/300
5/5 [==============================] - 0s 73ms/step - loss: 0.3916 - acc: 0.8820 - val_loss: 0.6680 - val_acc: 0.8137
Epoch 110/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3990 - acc: 0.8875 - val_loss: 0.6580 - val_acc: 0.8137
Epoch 111/300
5/5 [==============================] - 0s 95ms/step - loss: 0.4240 - acc: 0.8786 - val_loss: 0.6487 - val_acc: 0.8137
Epoch 112/300
5/5 [==============================] - 0s 67ms/step - loss: 0.4050 - acc: 0.8633 - val_loss: 0.6471 - val_acc: 0.8186
Epoch 113/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4120 - acc: 0.8522 - val_loss: 0.6375 - val_acc: 0.8137
Epoch 114/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3802 - acc: 0.8793 - val_loss: 0.6454 - val_acc: 0.8137
Epoch 115/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4073 - acc: 0.8730 - val_loss: 0.6504 - val_acc: 0.8088
Epoch 116/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3573 - acc: 0.8948 - val_loss: 0.6501 - val_acc: 0.7990
Epoch 117/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4238 - acc: 0.8611 - val_loss: 0.7339 - val_acc: 0.7843
Epoch 118/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3565 - acc: 0.8832 - val_loss: 0.7533 - val_acc: 0.7941
Epoch 119/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3863 - acc: 0.8834 - val_loss: 0.7470 - val_acc: 0.8186
Epoch 120/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3935 - acc: 0.8768 - val_loss: 0.6778 - val_acc: 0.8333
Epoch 121/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3745 - acc: 0.8862 - val_loss: 0.6741 - val_acc: 0.8137
Epoch 122/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4152 - acc: 0.8647 - val_loss: 0.6594 - val_acc: 0.8235
Epoch 123/300
5/5 [==============================] - 0s 64ms/step - loss: 0.3987 - acc: 0.8813 - val_loss: 0.6478 - val_acc: 0.8235
Epoch 124/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4005 - acc: 0.8798 - val_loss: 0.6837 - val_acc: 0.8284
Epoch 125/300
5/5 [==============================] - 0s 68ms/step - loss: 0.4366 - acc: 0.8699 - val_loss: 0.6456 - val_acc: 0.8235
Epoch 126/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3544 - acc: 0.8852 - val_loss: 0.6967 - val_acc: 0.8088
Epoch 127/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3835 - acc: 0.8676 - val_loss: 0.7279 - val_acc: 0.8088
Epoch 128/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3932 - acc: 0.8723 - val_loss: 0.7471 - val_acc: 0.8137
Epoch 129/300
5/5 [==============================] - 0s 66ms/step - loss: 0.3788 - acc: 0.8822 - val_loss: 0.7028 - val_acc: 0.8284
Epoch 130/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3546 - acc: 0.8876 - val_loss: 0.6424 - val_acc: 0.8382
Epoch 131/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4244 - acc: 0.8784 - val_loss: 0.6478 - val_acc: 0.8382
Epoch 132/300
5/5 [==============================] - 0s 66ms/step - loss: 0.4120 - acc: 0.8689 - val_loss: 0.6834 - val_acc: 0.8186
Epoch 133/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3585 - acc: 0.8872 - val_loss: 0.6802 - val_acc: 0.8186
Epoch 134/300
5/5 [==============================] - 0s 71ms/step - loss: 0.3782 - acc: 0.8788 - val_loss: 0.6936 - val_acc: 0.8235
Epoch 135/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3459 - acc: 0.8776 - val_loss: 0.6776 - val_acc: 0.8431
Epoch 136/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3176 - acc: 0.9108 - val_loss: 0.6881 - val_acc: 0.8382
Epoch 137/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3205 - acc: 0.9052 - val_loss: 0.6934 - val_acc: 0.8431
Epoch 138/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4079 - acc: 0.8782 - val_loss: 0.6830 - val_acc: 0.8431
Epoch 139/300
5/5 [==============================] - 0s 71ms/step - loss: 0.3465 - acc: 0.8973 - val_loss: 0.6876 - val_acc: 0.8431
Epoch 140/300
5/5 [==============================] - 0s 95ms/step - loss: 0.3935 - acc: 0.8766 - val_loss: 0.7166 - val_acc: 0.8382
Epoch 141/300
5/5 [==============================] - 0s 71ms/step - loss: 0.3905 - acc: 0.8868 - val_loss: 0.7320 - val_acc: 0.8284
Epoch 142/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3482 - acc: 0.8887 - val_loss: 0.7575 - val_acc: 0.8186
Epoch 143/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3567 - acc: 0.8820 - val_loss: 0.7537 - val_acc: 0.8235
Epoch 144/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3427 - acc: 0.8753 - val_loss: 0.7225 - val_acc: 0.8284
Epoch 145/300
5/5 [==============================] - 0s 72ms/step - loss: 0.3894 - acc: 0.8750 - val_loss: 0.7228 - val_acc: 0.8333
Epoch 146/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3585 - acc: 0.8938 - val_loss: 0.6870 - val_acc: 0.8284
Epoch 147/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3450 - acc: 0.8830 - val_loss: 0.6666 - val_acc: 0.8284
Epoch 148/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3174 - acc: 0.8929 - val_loss: 0.6683 - val_acc: 0.8382
Epoch 149/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3357 - acc: 0.9041 - val_loss: 0.6676 - val_acc: 0.8480
Epoch 150/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3597 - acc: 0.8792 - val_loss: 0.6913 - val_acc: 0.8235
Epoch 151/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3043 - acc: 0.9093 - val_loss: 0.7146 - val_acc: 0.8039
Epoch 152/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3935 - acc: 0.8814 - val_loss: 0.6716 - val_acc: 0.8382
Epoch 153/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3200 - acc: 0.8898 - val_loss: 0.6832 - val_acc: 0.8578
Epoch 154/300
5/5 [==============================] - 0s 71ms/step - loss: 0.3738 - acc: 0.8809 - val_loss: 0.6622 - val_acc: 0.8529
Epoch 155/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3784 - acc: 0.8777 - val_loss: 0.6510 - val_acc: 0.8431
Epoch 156/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3565 - acc: 0.8962 - val_loss: 0.6600 - val_acc: 0.8333
Epoch 157/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2935 - acc: 0.9137 - val_loss: 0.6732 - val_acc: 0.8333
Epoch 158/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3130 - acc: 0.9060 - val_loss: 0.7070 - val_acc: 0.8284
Epoch 159/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3386 - acc: 0.8937 - val_loss: 0.6865 - val_acc: 0.8480
Epoch 160/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3310 - acc: 0.9038 - val_loss: 0.7082 - val_acc: 0.8382
Epoch 161/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3232 - acc: 0.8993 - val_loss: 0.7184 - val_acc: 0.8431
Epoch 162/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3062 - acc: 0.9036 - val_loss: 0.7070 - val_acc: 0.8382
Epoch 163/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3374 - acc: 0.8962 - val_loss: 0.7187 - val_acc: 0.8284
Epoch 164/300
5/5 [==============================] - 0s 94ms/step - loss: 0.3249 - acc: 0.8977 - val_loss: 0.7197 - val_acc: 0.8382
Epoch 165/300
5/5 [==============================] - 0s 69ms/step - loss: 0.4041 - acc: 0.8764 - val_loss: 0.7195 - val_acc: 0.8431
Epoch 166/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3356 - acc: 0.9015 - val_loss: 0.7114 - val_acc: 0.8333
Epoch 167/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3006 - acc: 0.9017 - val_loss: 0.6988 - val_acc: 0.8235
Epoch 168/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3368 - acc: 0.8970 - val_loss: 0.6795 - val_acc: 0.8284
Epoch 169/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3049 - acc: 0.9124 - val_loss: 0.6590 - val_acc: 0.8333
Epoch 170/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3652 - acc: 0.8900 - val_loss: 0.6538 - val_acc: 0.8431
Epoch 171/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3153 - acc: 0.9094 - val_loss: 0.6342 - val_acc: 0.8480
Epoch 172/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2881 - acc: 0.9038 - val_loss: 0.6242 - val_acc: 0.8382
Epoch 173/300
5/5 [==============================] - 0s 66ms/step - loss: 0.3764 - acc: 0.8824 - val_loss: 0.6220 - val_acc: 0.8480
Epoch 174/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3352 - acc: 0.8958 - val_loss: 0.6305 - val_acc: 0.8578
Epoch 175/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3450 - acc: 0.9026 - val_loss: 0.6426 - val_acc: 0.8578
Epoch 176/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3471 - acc: 0.8941 - val_loss: 0.6653 - val_acc: 0.8333
Epoch 177/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3373 - acc: 0.8970 - val_loss: 0.6941 - val_acc: 0.8137
Epoch 178/300
5/5 [==============================] - 0s 69ms/step - loss: 0.2986 - acc: 0.9092 - val_loss: 0.6841 - val_acc: 0.8137
Epoch 179/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3466 - acc: 0.9038 - val_loss: 0.6704 - val_acc: 0.8284
Epoch 180/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3661 - acc: 0.8998 - val_loss: 0.6995 - val_acc: 0.8235
Epoch 181/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3163 - acc: 0.8902 - val_loss: 0.6806 - val_acc: 0.8235
Epoch 182/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3278 - acc: 0.9025 - val_loss: 0.6815 - val_acc: 0.8284
Epoch 183/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3343 - acc: 0.8960 - val_loss: 0.6704 - val_acc: 0.8333
Epoch 184/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3172 - acc: 0.8906 - val_loss: 0.6434 - val_acc: 0.8333
Epoch 185/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3679 - acc: 0.8921 - val_loss: 0.6394 - val_acc: 0.8529
Epoch 186/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3030 - acc: 0.9079 - val_loss: 0.6677 - val_acc: 0.8480
Epoch 187/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3102 - acc: 0.8908 - val_loss: 0.6456 - val_acc: 0.8529
Epoch 188/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2763 - acc: 0.9140 - val_loss: 0.6151 - val_acc: 0.8431
Epoch 189/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3298 - acc: 0.8964 - val_loss: 0.6119 - val_acc: 0.8676
Epoch 190/300
5/5 [==============================] - 0s 69ms/step - loss: 0.2928 - acc: 0.9094 - val_loss: 0.6141 - val_acc: 0.8480
Epoch 191/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3066 - acc: 0.9093 - val_loss: 0.6393 - val_acc: 0.8480
Epoch 192/300
5/5 [==============================] - 0s 94ms/step - loss: 0.2988 - acc: 0.9060 - val_loss: 0.6380 - val_acc: 0.8431
Epoch 193/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3654 - acc: 0.8800 - val_loss: 0.6102 - val_acc: 0.8578
Epoch 194/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3482 - acc: 0.8981 - val_loss: 0.6396 - val_acc: 0.8480
Epoch 195/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3029 - acc: 0.9083 - val_loss: 0.6410 - val_acc: 0.8431
Epoch 196/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3276 - acc: 0.8931 - val_loss: 0.6209 - val_acc: 0.8529
Epoch 197/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3252 - acc: 0.8989 - val_loss: 0.6153 - val_acc: 0.8578
Epoch 198/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3542 - acc: 0.8917 - val_loss: 0.6079 - val_acc: 0.8627
Epoch 199/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3191 - acc: 0.9006 - val_loss: 0.6087 - val_acc: 0.8578
Epoch 200/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3077 - acc: 0.9008 - val_loss: 0.6209 - val_acc: 0.8529
Epoch 201/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3045 - acc: 0.9076 - val_loss: 0.6609 - val_acc: 0.8333
Epoch 202/300
5/5 [==============================] - 0s 71ms/step - loss: 0.3053 - acc: 0.9058 - val_loss: 0.7324 - val_acc: 0.8284
Epoch 203/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3107 - acc: 0.8985 - val_loss: 0.7755 - val_acc: 0.8235
Epoch 204/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3047 - acc: 0.8995 - val_loss: 0.7936 - val_acc: 0.7941
Epoch 205/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3131 - acc: 0.9098 - val_loss: 0.6453 - val_acc: 0.8529
Epoch 206/300
5/5 [==============================] - 0s 71ms/step - loss: 0.3795 - acc: 0.8849 - val_loss: 0.6213 - val_acc: 0.8529
Epoch 207/300
5/5 [==============================] - 0s 70ms/step - loss: 0.2903 - acc: 0.9114 - val_loss: 0.6354 - val_acc: 0.8578
Epoch 208/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2599 - acc: 0.9164 - val_loss: 0.6390 - val_acc: 0.8676
Epoch 209/300
5/5 [==============================] - 0s 71ms/step - loss: 0.2954 - acc: 0.9041 - val_loss: 0.6376 - val_acc: 0.8775
Epoch 210/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3250 - acc: 0.9023 - val_loss: 0.6206 - val_acc: 0.8725
Epoch 211/300
5/5 [==============================] - 0s 69ms/step - loss: 0.2694 - acc: 0.9149 - val_loss: 0.6177 - val_acc: 0.8676
Epoch 212/300
5/5 [==============================] - 0s 71ms/step - loss: 0.2920 - acc: 0.9054 - val_loss: 0.6438 - val_acc: 0.8627
Epoch 213/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2861 - acc: 0.9048 - val_loss: 0.7128 - val_acc: 0.8480
Epoch 214/300
5/5 [==============================] - 0s 65ms/step - loss: 0.2916 - acc: 0.9083 - val_loss: 0.7030 - val_acc: 0.8431
Epoch 215/300
5/5 [==============================] - 0s 91ms/step - loss: 0.3288 - acc: 0.8887 - val_loss: 0.6593 - val_acc: 0.8529
Epoch 216/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3802 - acc: 0.8875 - val_loss: 0.6165 - val_acc: 0.8578
Epoch 217/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2905 - acc: 0.9175 - val_loss: 0.6141 - val_acc: 0.8725
Epoch 218/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3078 - acc: 0.9104 - val_loss: 0.6158 - val_acc: 0.8676
Epoch 219/300
5/5 [==============================] - 0s 66ms/step - loss: 0.2757 - acc: 0.9214 - val_loss: 0.6195 - val_acc: 0.8578
Epoch 220/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3159 - acc: 0.8958 - val_loss: 0.6375 - val_acc: 0.8578
Epoch 221/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3348 - acc: 0.8944 - val_loss: 0.6839 - val_acc: 0.8431
Epoch 222/300
5/5 [==============================] - 0s 70ms/step - loss: 0.3239 - acc: 0.8936 - val_loss: 0.6450 - val_acc: 0.8578
Epoch 223/300
5/5 [==============================] - 0s 73ms/step - loss: 0.2783 - acc: 0.9081 - val_loss: 0.6163 - val_acc: 0.8627
Epoch 224/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2852 - acc: 0.9165 - val_loss: 0.6495 - val_acc: 0.8431
Epoch 225/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3073 - acc: 0.8902 - val_loss: 0.6622 - val_acc: 0.8529
Epoch 226/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3127 - acc: 0.9102 - val_loss: 0.6652 - val_acc: 0.8431
Epoch 227/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3248 - acc: 0.9067 - val_loss: 0.6475 - val_acc: 0.8529
Epoch 228/300
5/5 [==============================] - 0s 69ms/step - loss: 0.3155 - acc: 0.9089 - val_loss: 0.6263 - val_acc: 0.8382
Epoch 229/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3585 - acc: 0.8898 - val_loss: 0.6308 - val_acc: 0.8578
Epoch 230/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2812 - acc: 0.9180 - val_loss: 0.6201 - val_acc: 0.8529
Epoch 231/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3070 - acc: 0.8984 - val_loss: 0.6170 - val_acc: 0.8431
Epoch 232/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3433 - acc: 0.8909 - val_loss: 0.6568 - val_acc: 0.8431
Epoch 233/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2844 - acc: 0.9085 - val_loss: 0.6571 - val_acc: 0.8529
Epoch 234/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3122 - acc: 0.9044 - val_loss: 0.6516 - val_acc: 0.8480
Epoch 235/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3047 - acc: 0.9232 - val_loss: 0.6505 - val_acc: 0.8480
Epoch 236/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2913 - acc: 0.9192 - val_loss: 0.6432 - val_acc: 0.8529
Epoch 237/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2505 - acc: 0.9322 - val_loss: 0.6462 - val_acc: 0.8627
Epoch 238/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3033 - acc: 0.9085 - val_loss: 0.6378 - val_acc: 0.8627
Epoch 239/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3418 - acc: 0.8975 - val_loss: 0.6232 - val_acc: 0.8578
Epoch 240/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3167 - acc: 0.9051 - val_loss: 0.6284 - val_acc: 0.8627
Epoch 241/300
5/5 [==============================] - 0s 69ms/step - loss: 0.2637 - acc: 0.9145 - val_loss: 0.6427 - val_acc: 0.8627
Epoch 242/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2678 - acc: 0.9227 - val_loss: 0.6492 - val_acc: 0.8578
Epoch 243/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2730 - acc: 0.9113 - val_loss: 0.6736 - val_acc: 0.8578
Epoch 244/300
5/5 [==============================] - 0s 93ms/step - loss: 0.3013 - acc: 0.9077 - val_loss: 0.7138 - val_acc: 0.8333
Epoch 245/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3151 - acc: 0.9096 - val_loss: 0.7278 - val_acc: 0.8382
Epoch 246/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3307 - acc: 0.9058 - val_loss: 0.6944 - val_acc: 0.8627
Epoch 247/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2631 - acc: 0.9236 - val_loss: 0.6789 - val_acc: 0.8529
Epoch 248/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3215 - acc: 0.9027 - val_loss: 0.6790 - val_acc: 0.8529
Epoch 249/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2968 - acc: 0.9038 - val_loss: 0.6864 - val_acc: 0.8480
Epoch 250/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2998 - acc: 0.9078 - val_loss: 0.7079 - val_acc: 0.8480
Epoch 251/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2375 - acc: 0.9197 - val_loss: 0.7252 - val_acc: 0.8529
Epoch 252/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2955 - acc: 0.9178 - val_loss: 0.7298 - val_acc: 0.8284
Epoch 253/300
5/5 [==============================] - 0s 69ms/step - loss: 0.2946 - acc: 0.9039 - val_loss: 0.7172 - val_acc: 0.8284
Epoch 254/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3051 - acc: 0.9087 - val_loss: 0.6861 - val_acc: 0.8382
Epoch 255/300
5/5 [==============================] - 0s 67ms/step - loss: 0.3563 - acc: 0.8882 - val_loss: 0.6739 - val_acc: 0.8480
Epoch 256/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3144 - acc: 0.8969 - val_loss: 0.6970 - val_acc: 0.8382
Epoch 257/300
5/5 [==============================] - 0s 68ms/step - loss: 0.3210 - acc: 0.9152 - val_loss: 0.7106 - val_acc: 0.8333
Epoch 258/300
5/5 [==============================] - 0s 67ms/step - loss: 0.2523 - acc: 0.9214 - val_loss: 0.7111 - val_acc: 0.8431
Epoch 259/300
5/5 [==============================] - 0s 68ms/step - loss: 0.2552 - acc: 0.9236 - val_loss: 0.7258 - val_acc: 0.8382
让我们绘制学习曲线
display_learning_curves(history)
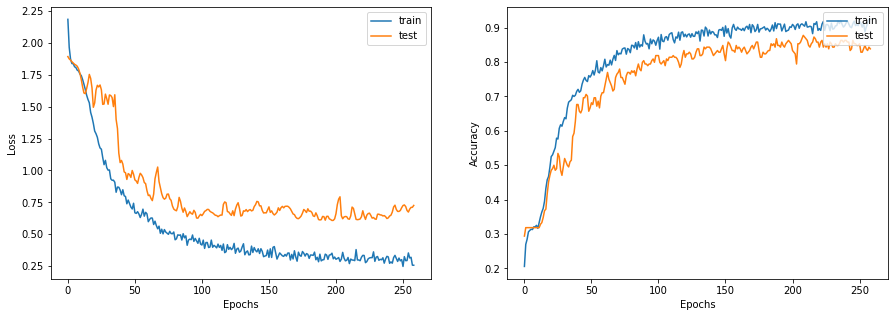
现在我们在测试数据集上评估GNN模型。 结果可能会因训练样本而异,但是GNN模型在测试准确度上始终优于基线模型。
x_test = test_data.paper_id.to_numpy()
_, test_accuracy = gnn_model.evaluate(x=x_test, y=y_test, verbose=0)
print(f"测试准确率: {round(test_accuracy * 100, 2)}%")
测试准确率: 80.19%
检查GNN模型预测
让我们将新实例作为节点添加到node_features中,并生成链接
(引用)到现有节点。
# 首先我们将 N 个新实例作为节点添加到图中
# 通过将 new_instance 附加到 node_features。
num_nodes = node_features.shape[0]
new_node_features = np.concatenate([node_features, new_instances])
# 其次,我们将 M 条边(引用)从每个新节点添加到
# 特定学科中的一组现有节点
new_node_indices = [i + num_nodes for i in range(num_classes)]
new_citations = []
for subject_idx, group in papers.groupby("subject"):
subject_papers = list(group.paper_id)
# 选择特定学科的随机 x 篇论文。
selected_paper_indices1 = np.random.choice(subject_papers, 5)
# 从任何学科中选择随机 y 篇论文(其中 y < x)。
selected_paper_indices2 = np.random.choice(list(papers.paper_id), 2)
# 合并所选论文索引。
selected_paper_indices = np.concatenate(
[selected_paper_indices1, selected_paper_indices2], axis=0
)
# 在引用论文索引和所选被引用论文之间创建边。
citing_paper_indx = new_node_indices[subject_idx]
for cited_paper_idx in selected_paper_indices:
new_citations.append([citing_paper_indx, cited_paper_idx])
new_citations = np.array(new_citations).T
new_edges = np.concatenate([edges, new_citations], axis=1)
现在让我们更新GNN模型中的node_features和edges。
print("原始 node_features 形状:", gnn_model.node_features.shape)
print("原始 edges 形状:", gnn_model.edges.shape)
gnn_model.node_features = new_node_features
gnn_model.edges = new_edges
gnn_model.edge_weights = tf.ones(shape=new_edges.shape[1])
print("新 node_features 形状:", gnn_model.node_features.shape)
print("新 edges 形状:", gnn_model.edges.shape)
logits = gnn_model.predict(tf.convert_to_tensor(new_node_indices))
probabilities = keras.activations.softmax(tf.convert_to_tensor(logits)).numpy()
display_class_probabilities(probabilities)
原始 node_features 形状: (2708, 1433)
原始 edges 形状: (2, 5429)
新 node_features 形状: (2715, 1433)
新 edges 形状: (2, 5478)
实例 1:
- 基于案例: 4.35%
- 遗传算法: 4.19%
- 神经网络: 1.49%
- 概率方法: 1.68%
- 强化学习: 21.34%
- 规则学习: 52.82%
- 理论: 14.14%
实例 2:
- 基于案例: 0.01%
- 遗传算法: 99.88%
- 神经网络: 0.03%
- 概率方法: 0.0%
- 强化学习: 0.07%
- 规则学习: 0.0%
- 理论: 0.01%
实例 3:
- 基于案例: 0.1%
- 遗传算法: 59.18%
- 神经网络: 39.17%
- 概率方法: 0.38%
- 强化学习: 0.55%
- 规则学习: 0.08%
- 理论: 0.54%
实例 4:
- 基于案例: 0.14%
- 遗传算法: 10.44%
- 神经网络: 84.1%
- 概率方法: 3.61%
- 强化学习: 0.71%
- 规则学习: 0.16%
- 理论: 0.85%
实例 5:
- 基于案例: 0.27%
- 遗传算法: 0.15%
- 神经网络: 0.48%
- 概率方法: 0.23%
- 强化学习: 0.79%
- 规则学习: 0.45%
- 理论: 97.63%
实例 6:
- 基于案例: 3.12%
- 遗传算法: 1.35%
- 神经网络: 19.72%
- 概率方法: 0.48%
- 强化学习: 39.56%
- 规则学习: 28.0%
- 理论: 7.77%
实例 7:
- 基于案例: 1.6%
- 遗传算法: 34.76%
- 神经网络: 4.45%
- 概率方法: 9.59%
- 强化学习: 2.97%
- 规则学习: 4.05%
- 理论: 42.6%
注意到预期学科的概率 (添加了多个引用的学科)高于基线模型。
