使用混合密度网络逼近非函数映射
作者: lukewood
创建日期: 2023/07/15
最后修改: 2023/07/15
描述: 使用混合密度网络逼近非单一映射。
逼近非函数
神经网络是通用函数逼近器。关键字:函数!
虽然神经网络是强大的函数逼近器,但它们无法逼近非函数。
一个重要的限制是,函数 - 它们有一个输入,一个输出!
当训练集中,对于单个 X 存在多个 Y 的情况下,神经网络受到很大影响。
在本指南中,我将向您展示如何逼近由 x -> y 映射组成的非函数类,以便给定的 x 可能存在多个 y。我们将使用一种称为“混合密度网络”的神经网络类别。
我将使用新的 多后端 Keras Core 项目 来构建我的混合密度网络。
Keras 团队在这个项目上做得很棒 - 能够用一行代码更换框架太棒了。
一些坏消息:我在本指南中使用 TensorFlow 概率……所以它实际上无法与其他后端配合使用。
无论如何,让我们开始安装依赖并整理导入:
!pip install -q --upgrade tensorflow-probability keras-core
import numpy as np
import matplotlib.pyplot as plt
import math
import random
from keras_core import callbacks
import keras_core
import tensorflow as tf
from keras_core import layers
from keras_core import optimizers
from tensorflow_probability import distributions as tfd
使用 TensorFlow 后端
接下来,让我们生成一个嘈杂的螺旋形,我们将尝试逼近。
我在下面定义了一些函数来实现这一点:
def normalize(x):
return (x - np.min(x)) / (np.max(x) - np.min(x))
def create_noisy_spiral(n, jitter_std=0.2, revolutions=2):
angle = np.random.uniform(0, 2 * np.pi * revolutions, [n])
r = angle
x = r * np.cos(angle)
y = r * np.sin(angle)
result = np.stack([x, y], axis=1)
result = result + np.random.normal(scale=jitter_std, size=[n, 2])
result = 5 * normalize(result)
return result
接下来,让我们多次调用此函数来构建一个样本数据集:
xy = create_noisy_spiral(10000)
x, y = xy[:, 0:1], xy[:, 1:]
plt.scatter(x, y)
plt.show()

正如您所看到的,给定的 X 存在多个可能的 Y 值。
普通的神经网络将简单地学习这些点在几何空间中的均值。
我们可以用一个简单的线性模型快速展示这一点:
N_HIDDEN = 128
model = keras_core.Sequential(
[
layers.Dense(N_HIDDEN, activation="relu"),
layers.Dense(N_HIDDEN, activation="relu"),
layers.Dense(1),
]
)
让我们使用均方误差以及 Adam 优化器。
这些通常是合理的原型选择:
model.compile(optimizer="adam", loss="mse")
我们可以很容易地拟合这个模型:
model.fit(
x,
y,
epochs=300,
batch_size=128,
validation_split=0.15,
callbacks=[callbacks.EarlyStopping(monitor="val_loss", patience=10)],
)
Epoch 1/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 3s 8ms/step - loss: 2.6971 - val_loss: 1.6366
Epoch 2/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.5672 - val_loss: 1.2341
Epoch 3/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.1751 - val_loss: 1.0113
Epoch 4/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0322 - val_loss: 1.0108
Epoch 5/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0625 - val_loss: 1.0212
Epoch 6/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0290 - val_loss: 1.0022
Epoch 7/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0469 - val_loss: 1.0033
Epoch 8/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0247 - val_loss: 1.0011
Epoch 9/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0313 - val_loss: 0.9997
Epoch 10/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0252 - val_loss: 0.9995
Epoch 11/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0369 - val_loss: 1.0015
Epoch 12/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0203 - val_loss: 0.9958
Epoch 13/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0305 - val_loss: 0.9960
Epoch 14/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0283 - val_loss: 1.0081
Epoch 15/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0331 - val_loss: 0.9943
Epoch 16/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 1.0244 - val_loss: 1.0021
Epoch 17/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0496 - val_loss: 1.0077
Epoch 18/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0367 - val_loss: 0.9940
Epoch 19/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0201 - val_loss: 0.9927
Epoch 20/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0501 - val_loss: 1.0133
Epoch 21/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0098 - val_loss: 0.9980
Epoch 22/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0195 - val_loss: 0.9907
Epoch 23/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0196 - val_loss: 0.9899
Epoch 24/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0170 - val_loss: 1.0033
Epoch 25/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0169 - val_loss: 0.9963
Epoch 26/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0141 - val_loss: 0.9895
Epoch 27/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0367 - val_loss: 0.9916
Epoch 28/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0301 - val_loss: 0.9991
Epoch 29/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0097 - val_loss: 1.0004
Epoch 30/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0415 - val_loss: 1.0062
Epoch 31/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0186 - val_loss: 0.9888
Epoch 32/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0230 - val_loss: 0.9910
Epoch 33/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0217 - val_loss: 0.9910
Epoch 34/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0180 - val_loss: 0.9945
Epoch 35/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0329 - val_loss: 0.9963
Epoch 36/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0190 - val_loss: 0.9912
Epoch 37/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0341 - val_loss: 0.9894
Epoch 38/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0100 - val_loss: 0.9920
Epoch 39/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0097 - val_loss: 0.9899
Epoch 40/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0216 - val_loss: 0.9948
Epoch 41/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0115 - val_loss: 0.9923
<keras_core.src.callbacks.history.History at 0x12e0b4dd0>
让我们看看结果:
y_pred = model.predict(x) # 模型预测
313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 851us/step
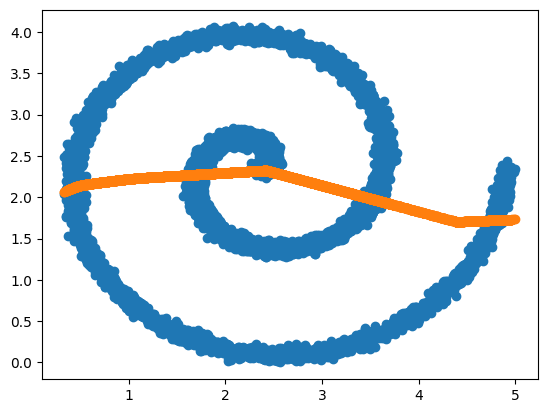
正如预期的那样,模型学习了给定 x 的所有点在 y 中的几何平均值。
plt.scatter(x, y) # 绘制真实值散点图
plt.scatter(x, y_pred) # 绘制预测值散点图
plt.show()
混合密度网络
混合密度网络可以缓解这个问题。
混合密度是一类可用较简单密度表达的复杂密度。
它们实际上是大量概率分布的总和。
混合密度网络学习根据给定的训练集参数化混合密度分布。
作为从业者,您只需要知道混合密度网络解决了给定 X 的多重 Y 值问题。
我希望为您的工具包添加一个工具——但我不会在本指南中正式解释混合密度网络的推导。
最重要的是,混合密度网络学习如何参数化混合密度分布。
这是通过计算针对提供的 y_i 标签以及对应的 x_i 的预测分布的特殊损失来完成的。
该损失函数通过计算 y_i 从预测混合分布中抽取的概率来运作。
让我们实现一个混合密度网络。
下面定义了一堆基于旧的 Keras 库的助手函数 Keras Mixture Density Network Layer。
我已经调整了代码以便与 Keras 核心一起使用。
让我们开始编写混合密度网络!
首先,我们需要一个特殊的激活函数:ELU 加上一个小的 epsilon。
这有助于防止 ELU 输出 0,从而导致混合密度网络损失评估中的 NaN。
def elu_plus_one_plus_epsilon(x):
return keras_core.activations.elu(x) + 1 + keras_core.backend.epsilon() # ELU 加一加 epsilon
接下来,让我们实际定义一个混合密度输出层,该层输出从学习到的混合分布中采样所需的所有值:
class MixtureDensityOutput(layers.Layer):
def __init__(self, output_dimension, num_mixtures, **kwargs):
super().__init__(**kwargs)
self.output_dim = output_dimension
self.num_mix = num_mixtures
self.mdn_mus = layers.Dense(
self.num_mix * self.output_dim, name="mdn_mus"
) # mix*output 值,无激活
self.mdn_sigmas = layers.Dense(
self.num_mix * self.output_dim,
activation=elu_plus_one_plus_epsilon,
name="mdn_sigmas",
) # mix*output 值,指数激活
self.mdn_pi = layers.Dense(self.num_mix, name="mdn_pi") # mix 值,logits
def build(self, input_shape):
self.mdn_mus.build(input_shape)
self.mdn_sigmas.build(input_shape)
self.mdn_pi.build(input_shape)
super().build(input_shape)
@property
def trainable_weights(self):
return (
self.mdn_mus.trainable_weights
+ self.mdn_sigmas.trainable_weights
+ self.mdn_pi.trainable_weights
)
@property
def non_trainable_weights(self):
return (
self.mdn_mus.non_trainable_weights
+ self.mdn_sigmas.non_trainable_weights
+ self.mdn_pi.non_trainable_weights
)
def call(self, x, mask=None):
return layers.concatenate(
[self.mdn_mus(x), self.mdn_sigmas(x), self.mdn_pi(x)], name="mdn_outputs" # 返回混合密度输出
)
让我们使用我们的新层构建一个混合密度网络:
OUTPUT_DIMS = 1
N_MIXES = 20
mdn_network = keras_core.Sequential(
[
layers.Dense(N_HIDDEN, activation="relu"), # 隐藏层
layers.Dense(N_HIDDEN, activation="relu"), # 隐藏层
MixtureDensityOutput(OUTPUT_DIMS, N_MIXES), # 混合密度输出层
]
)
接下来,让我们实现一个自定义损失函数,以根据真实值和我们期望的输出训练混合密度网络层:
def get_mixture_loss_func(output_dim, num_mixes):
def mdn_loss_func(y_true, y_pred):
# 在可能用于 TimeDistributed 层的情况下重塑输入
y_pred = tf.reshape(
y_pred,
[-1, (2 * num_mixes * output_dim) + num_mixes],
name="reshape_ypreds",
)
y_true = tf.reshape(y_true, [-1, output_dim], name="reshape_ytrue")
# 将输入拆分为参数
out_mu, out_sigma, out_pi = tf.split(
y_pred,
num_or_size_splits=[
num_mixes * output_dim,
num_mixes * output_dim,
num_mixes,
],
axis=-1,
name="mdn_coef_split",
)
# 构建混合模型
cat = tfd.Categorical(logits=out_pi)
component_splits = [output_dim] * num_mixes
mus = tf.split(out_mu, num_or_size_splits=component_splits, axis=1)
sigs = tf.split(out_sigma, num_or_size_splits=component_splits, axis=1)
coll = [
tfd.MultivariateNormalDiag(loc=loc, scale_diag=scale)
for loc, scale in zip(mus, sigs)
]
mixture = tfd.Mixture(cat=cat, components=coll)
loss = mixture.log_prob(y_true)
loss = tf.negative(loss)
loss = tf.reduce_mean(loss)
return loss
return mdn_loss_func
mdn_network.compile(loss=get_mixture_loss_func(OUTPUT_DIMS, N_MIXES), optimizer="adam")
最后,我们可以像其他Keras模型一样调用model.fit()。
mdn_network.fit(
x,
y,
epochs=300,
batch_size=128,
validation_split=0.15,
callbacks=[
callbacks.EarlyStopping(monitor="loss", patience=10, restore_best_weights=True), # 提前停止监控损失,耐心为10,恢复最佳权重
callbacks.ReduceLROnPlateau(monitor="loss", patience=5), # 减少学习率,如果损失在5个epoch内没有改善
],
)
Epoch 1/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 20s 89ms/step - loss: 2.5088 - val_loss: 1.6384 - learning_rate: 0.0010
Epoch 2/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.5954 - val_loss: 1.4872 - learning_rate: 0.0010
Epoch 3/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.4818 - val_loss: 1.4026 - learning_rate: 0.0010
Epoch 4/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.3818 - val_loss: 1.3327 - learning_rate: 0.0010
Epoch 5/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.3478 - val_loss: 1.3034 - learning_rate: 0.0010
Epoch 6/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 1.3045 - val_loss: 1.2684 - learning_rate: 0.0010
Epoch 7/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 1.2836 - val_loss: 1.2381 - learning_rate: 0.0010
Epoch 8/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 1.2582 - val_loss: 1.2047 - learning_rate: 0.0010
Epoch 9/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.2212 - val_loss: 1.1915 - learning_rate: 0.0010
Epoch 10/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.1907 - val_loss: 1.1903 - learning_rate: 0.0010
Epoch 11/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.1456 - val_loss: 1.0221 - learning_rate: 0.0010
Epoch 12/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.0075 - val_loss: 0.9356 - learning_rate: 0.0010
Epoch 13/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.9413 - val_loss: 0.8409 - learning_rate: 0.0010
Epoch 14/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.8646 - val_loss: 0.8717 - learning_rate: 0.0010
Epoch 15/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.8053 - val_loss: 0.8080 - learning_rate: 0.0010
Epoch 16/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.7568 - val_loss: 0.6381 - learning_rate: 0.0010
Epoch 17/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.6638 - val_loss: 0.6175 - learning_rate: 0.0010
Epoch 18/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.5893 - val_loss: 0.5387 - learning_rate: 0.0010
Epoch 19/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.5835 - val_loss: 0.5449 - learning_rate: 0.0010
Epoch 20/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.5137 - val_loss: 0.4536 - learning_rate: 0.0010
Epoch 21/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.4808 - val_loss: 0.4779 - learning_rate: 0.0010
Epoch 22/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.4592 - val_loss: 0.4359 - learning_rate: 0.0010
Epoch 23/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.4303 - val_loss: 0.4768 - learning_rate: 0.0010
Epoch 24/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.4505 - val_loss: 0.4084 - learning_rate: 0.0010
Epoch 25/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.4033 - val_loss: 0.3484 - learning_rate: 0.0010
Epoch 26/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.3696 - val_loss: 0.4844 - learning_rate: 0.0010
Epoch 27/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.3868 - val_loss: 0.3406 - learning_rate: 0.0010
Epoch 28/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.3214 - val_loss: 0.2739 - learning_rate: 0.0010
Epoch 29/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.3154 - val_loss: 0.3286 - learning_rate: 0.0010
Epoch 30/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.2930 - val_loss: 0.2263 - learning_rate: 0.0010
Epoch 31/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.2946 - val_loss: 0.2927 - learning_rate: 0.0010
Epoch 32/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.2739 - val_loss: 0.2026 - learning_rate: 0.0010
Epoch 33/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.2454 - val_loss: 0.2451 - learning_rate: 0.0010
Epoch 34/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.2146 - val_loss: 0.1722 - learning_rate: 0.0010
Epoch 35/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.2041 - val_loss: 0.2774 - learning_rate: 0.0010
Epoch 36/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.2020 - val_loss: 0.1257 - learning_rate: 0.0010
Epoch 37/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.1614 - val_loss: 0.1128 - learning_rate: 0.0010
Epoch 38/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.1676 - val_loss: 0.1908 - learning_rate: 0.0010
Epoch 39/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.1511 - val_loss: 0.1045 - learning_rate: 0.0010
Epoch 40/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.1061 - val_loss: 0.1321 - learning_rate: 0.0010
Epoch 41/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.1170 - val_loss: 0.0879 - learning_rate: 0.0010
Epoch 42/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.1045 - val_loss: 0.0307 - learning_rate: 0.0010
Epoch 43/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.1066 - val_loss: 0.0637 - learning_rate: 0.0010
Epoch 44/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0960 - val_loss: 0.0304 - learning_rate: 0.0010
Epoch 45/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0747 - val_loss: 0.0211 - learning_rate: 0.0010
Epoch 46/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0733 - val_loss: -0.0155 - learning_rate: 0.0010
Epoch 47/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0339 - val_loss: 0.0079 - learning_rate: 0.0010
Epoch 48/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0597 - val_loss: 0.0223 - learning_rate: 0.0010
Epoch 49/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0370 - val_loss: 0.0549 - learning_rate: 0.0010
Epoch 50/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0343 - val_loss: 0.0031 - learning_rate: 0.0010
Epoch 51/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0132 - val_loss: -0.0304 - learning_rate: 0.0010
Epoch 52/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0326 - val_loss: 0.0584 - learning_rate: 0.0010
Epoch 53/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0512 - val_loss: -0.0166 - learning_rate: 0.0010
Epoch 54/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0210 - val_loss: -0.0433 - learning_rate: 0.0010
Epoch 55/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0261 - val_loss: 0.0317 - learning_rate: 0.0010
Epoch 56/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0185 - val_loss: -0.0210 - learning_rate: 0.0010
Epoch 57/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0021 - val_loss: -0.0218 - learning_rate: 0.0010
Epoch 58/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0100 - val_loss: -0.0488 - learning_rate: 0.0010
Epoch 59/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0126 - val_loss: -0.0504 - learning_rate: 0.0010
Epoch 60/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0278 - val_loss: -0.0622 - learning_rate: 0.0010
Epoch 61/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0180 - val_loss: -0.0756 - learning_rate: 0.0010
Epoch 62/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: -0.0198 - val_loss: -0.0427 - learning_rate: 0.0010
Epoch 63/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0129 - val_loss: -0.0483 - learning_rate: 0.0010
Epoch 64/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0221 - val_loss: -0.0379 - learning_rate: 0.0010
Epoch 65/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: -0.0177 - val_loss: -0.0626 - learning_rate: 0.0010
Epoch 66/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0045 - val_loss: -0.0148 - learning_rate: 0.0010
Epoch 67/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0045 - val_loss: -0.0570 - learning_rate: 0.0010
Epoch 68/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0304 - val_loss: -0.0062 - learning_rate: 0.0010
Epoch 69/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0053 - val_loss: -0.0553 - learning_rate: 0.0010
Epoch 70/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0364 - val_loss: -0.1112 - learning_rate: 0.0010
Epoch 71/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0017 - val_loss: -0.0865 - learning_rate: 0.0010
Epoch 72/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0082 - val_loss: -0.1180 - learning_rate: 0.0010
Epoch 73/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0501 - val_loss: -0.1028 - learning_rate: 0.0010
Epoch 74/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0452 - val_loss: -0.0381 - learning_rate: 0.0010
Epoch 75/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0397 - val_loss: -0.0517 - learning_rate: 0.0010
Epoch 76/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0317 - val_loss: -0.1144 - learning_rate: 0.0010
Epoch 77/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0400 - val_loss: -0.1283 - learning_rate: 0.0010
Epoch 78/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0756 - val_loss: -0.0749 - learning_rate: 0.0010
Epoch 79/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0459 - val_loss: -0.1229 - learning_rate: 0.0010
Epoch 80/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0485 - val_loss: -0.0896 - learning_rate: 0.0010
Epoch 81/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: -0.0351 - val_loss: -0.1037 - learning_rate: 0.0010
Epoch 82/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0617 - val_loss: -0.0949 - learning_rate: 0.0010
Epoch 83/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0614 - val_loss: -0.1044 - learning_rate: 0.0010
Epoch 84/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0650 - val_loss: -0.1128 - learning_rate: 0.0010
Epoch 85/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0710 - val_loss: -0.1236 - learning_rate: 0.0010
Epoch 86/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0504 - val_loss: -0.0149 - learning_rate: 0.0010
Epoch 87/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0561 - val_loss: -0.1095 - learning_rate: 0.0010
Epoch 88/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0527 - val_loss: -0.0929 - learning_rate: 0.0010
Epoch 89/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0704 - val_loss: -0.1062 - learning_rate: 0.0010
Epoch 90/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.0386 - val_loss: -0.1433 - learning_rate: 0.0010
Epoch 91/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1129 - val_loss: -0.1698 - learning_rate: 1.0000e-04
Epoch 92/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1210 - val_loss: -0.1696 - learning_rate: 1.0000e-04
Epoch 93/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1315 - val_loss: -0.1663 - learning_rate: 1.0000e-04
Epoch 94/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1207 - val_loss: -0.1696 - learning_rate: 1.0000e-04
Epoch 95/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1208 - val_loss: -0.1606 - learning_rate: 1.0000e-04
Epoch 96/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1157 - val_loss: -0.1728 - learning_rate: 1.0000e-04
Epoch 97/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1367 - val_loss: -0.1691 - learning_rate: 1.0000e-04
Epoch 98/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1237 - val_loss: -0.1740 - learning_rate: 1.0000e-04
Epoch 99/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1271 - val_loss: -0.1593 - learning_rate: 1.0000e-04
Epoch 100/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1358 - val_loss: -0.1738 - learning_rate: 1.0000e-04
Epoch 101/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1260 - val_loss: -0.1669 - learning_rate: 1.0000e-04
Epoch 102/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1184 - val_loss: -0.1660 - learning_rate: 1.0000e-04
Epoch 103/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1221 - val_loss: -0.1740 - learning_rate: 1.0000e-04
Epoch 104/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1207 - val_loss: -0.1498 - learning_rate: 1.0000e-04
Epoch 105/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1210 - val_loss: -0.1695 - learning_rate: 1.0000e-04
Epoch 106/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1264 - val_loss: -0.1477 - learning_rate: 1.0000e-04
Epoch 107/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1217 - val_loss: -0.1717 - learning_rate: 1.0000e-04
Epoch 108/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1182 - val_loss: -0.1748 - learning_rate: 1.0000e-05
Epoch 109/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1394 - val_loss: -0.1757 - learning_rate: 1.0000e-05
Epoch 110/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1363 - val_loss: -0.1762 - learning_rate: 1.0000e-05
Epoch 111/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1292 - val_loss: -0.1765 - learning_rate: 1.0000e-05
Epoch 112/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1330 - val_loss: -0.1737 - learning_rate: 1.0000e-05
Epoch 113/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1341 - val_loss: -0.1769 - learning_rate: 1.0000e-05
Epoch 114/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1318 - val_loss: -0.1771 - learning_rate: 1.0000e-05
Epoch 115/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1285 - val_loss: -0.1756 - learning_rate: 1.0000e-05
Epoch 116/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1211 - val_loss: -0.1764 - learning_rate: 1.0000e-05
Epoch 117/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1434 - val_loss: -0.1755 - learning_rate: 1.0000e-05
Epoch 118/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - loss: -0.1375 - val_loss: -0.1757 - learning_rate: 1.0000e-05
Epoch 119/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1407 - val_loss: -0.1740 - learning_rate: 1.0000e-05
Epoch 120/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1406 - val_loss: -0.1754 - learning_rate: 1.0000e-06
Epoch 121/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1258 - val_loss: -0.1761 - learning_rate: 1.0000e-06
Epoch 122/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1384 - val_loss: -0.1762 - learning_rate: 1.0000e-06
Epoch 123/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1522 - val_loss: -0.1764 - learning_rate: 1.0000e-06
Epoch 124/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1310 - val_loss: -0.1763 - learning_rate: 1.0000e-06
Epoch 125/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1434 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 126/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1329 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 127/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1392 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 128/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1300 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 129/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: -0.1347 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 130/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: -0.1200 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 131/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: -0.1415 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 132/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1270 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 133/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1329 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 134/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1265 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 135/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1329 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 136/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1429 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 137/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1394 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 138/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1315 - val_loss: -0.1763 - learning_rate: 1.0000e-07
Epoch 139/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1253 - val_loss: -0.1763 - learning_rate: 1.0000e-08
Epoch 140/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1346 - val_loss: -0.1763 - learning_rate: 1.0000e-08
Epoch 141/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1418 - val_loss: -0.1763 - learning_rate: 1.0000e-08
Epoch 142/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: -0.1279 - val_loss: -0.1763 - learning_rate: 1.0000e-08
Epoch 143/300
67/67 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: -0.1224 - val_loss: -0.1763 - learning_rate: 1.0000e-08
<keras_core.src.callbacks.history.History at 0x148c20890>
让我们做一些预测!
y_pred_mixture = mdn_network.predict(x)
print(y_pred_mixture.shape)
313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 811us/step
(10000, 60)
MDN不会输出一个单一的值;而是输出用于参数化混合分布的值。 为了可视化这些输出,让我们从分布中进行采样。
请注意,采样是一个有损过程。 如果您希望将所有信息作为更大潜在表示的一部分保留(即用于下游处理),我建议您只是保留分布参数不变。
def split_mixture_params(params, output_dim, num_mixes):
mus = params[: num_mixes * output_dim]
sigs = params[num_mixes * output_dim : 2 * num_mixes * output_dim]
pi_logits = params[-num_mixes:]
return mus, sigs, pi_logits
def softmax(w, t=1.0):
e = np.array(w) / t # 调整温度
e -= e.max() # 减去最大值以防止指数值溢出
e = np.exp(e)
dist = e / np.sum(e)
return dist
def sample_from_categorical(dist):
r = np.random.rand(1) # [0,1]中的均匀随机数
accumulate = 0
for i in range(0, dist.size):
accumulate += dist[i]
if accumulate >= r:
return i
tf.logging.info("分类模型采样错误。")
return -1
def sample_from_output(params, output_dim, num_mixes, temp=1.0, sigma_temp=1.0):
mus, sigs, pi_logits = split_mixture_params(params, output_dim, num_mixes)
pis = softmax(pi_logits, t=temp)
m = sample_from_categorical(pis)
# 另一种从分类中采样的方法:
# m = np.random.choice(range(len(pis)), p=pis)
mus_vector = mus[m * output_dim : (m + 1) * output_dim]
sig_vector = sigs[m * output_dim : (m + 1) * output_dim]
scale_matrix = np.identity(output_dim) * sig_vector # 从对角线获取缩放矩阵
cov_matrix = np.matmul(scale_matrix, scale_matrix.T) # 协方差是缩放的平方
cov_matrix = cov_matrix * sigma_temp # 调整sigma温度
sample = np.random.multivariate_normal(mus_vector, cov_matrix, 1)
return sample
接下来,让我们使用我们的采样函数:
# 从预测的分布中采样
y_samples = np.apply_along_axis(
sample_from_output, 1, y_pred_mixture, 1, N_MIXES, temp=1.0
)
最后,我们可以可视化我们的网络输出
plt.scatter(x, y, alpha=0.05, color="blue", label="真实值")
plt.scatter(
x,
y_samples[:, :, 0],
color="green",
alpha=0.05,
label="混合密度网络预测",
)
plt.show()
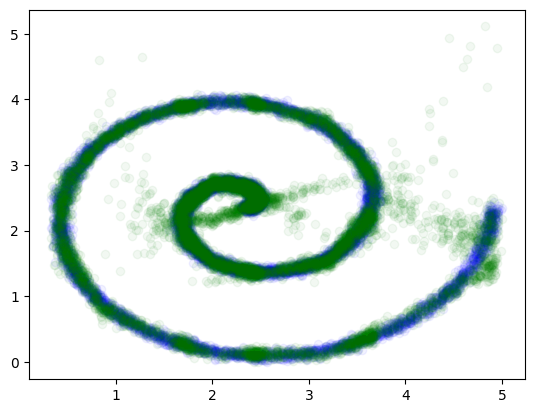
漂亮。 真高兴看到这一点
结论
神经网络是通用的函数逼近器——但它们只能逼近函数。混合密度网络可以使用一些巧妙的概率技巧逼近任意x->y映射。
有关更多使用 tensorflow_probability 的示例
从这里开始。
再来一个漂亮的图形作为结束:
fig, axs = plt.subplots(1, 3)
fig.set_figheight(3)
fig.set_figwidth(12)
axs[0].set_title("真实值")
axs[0].scatter(x, y, alpha=0.05, color="blue")
xlim = axs[0].get_xlim()
ylim = axs[0].get_ylim()
axs[1].set_title("正态模型预测")
axs[1].scatter(x, y_pred, alpha=0.05, color="red")
axs[1].set_xlim(xlim)
axs[1].set_ylim(ylim)
axs[2].scatter(
x,
y_samples[:, :, 0],
color="green",
alpha=0.05,
label="混合密度网络预测",
)
axs[2].set_title("混合密度网络预测")
axs[2].set_xlim(xlim)
axs[2].set_ylim(ylim)
plt.show()

