► 代码示例 / 快速Keras食谱 / Keras 调试技巧

Keras 调试技巧

作者: fchollet
创建日期: 2020/05/16
最后修改: 2023/11/16
描述: 四个简单的技巧帮助你调试 Keras 代码。

介绍

在 Keras 中，通常可以无需编写代码做几乎所有事情：无论你是在实现一种新的 GAN 类型还是最新的用于图像分割的卷积神经网络架构，你通常都可以调用内置的方法。由于所有内置方法都进行了广泛的输入验证检查，因此你几乎不用进行调试。完全由内置层构建的函数式 API 模型通常能第一次就成功运行——只要你能编译它，它就能运行。

然而，有时你需要深入挖掘，编写自己的代码。以下是一些常见的例子：

创建一个新的 Layer 子类。
创建一个自定义的 Metric 子类。
在 Model 上实现自定义的 train_step。

本文档提供了一些简单的技巧，帮助你在这些情况下进行调试。

技巧 1: 在测试整个模型之前先测试每个部分

如果你创建的任何对象有可能无法按预期工作，不要只是把它放入端到端的过程并看着它出错。相反，先单独测试你的自定义对象。这看起来似乎是显而易见的——但你会惊讶于人们有多么常常忽视这一点。

如果你编写了一个自定义层，不要现在就对整个模型调用 fit()。先在一些测试数据上调用你的层。
如果你编写了一个自定义指标，首先打印一些参考输入的输出。

这是一个简单的例子。让我们编写一个自定义层并在其中引入一个错误：

import os

# 最后的示例使用了 tf.GradientTape，因此需要 TensorFlow。
# 然而，这里的所有技巧都适用于所有后端。
os.environ["KERAS_BACKEND"] = "tensorflow"

import keras
from keras import layers
from keras import ops
import numpy as np
import tensorflow as tf


class MyAntirectifier(layers.Layer):
    def build(self, input_shape):
        output_dim = input_shape[-1]
        self.kernel = self.add_weight(
            shape=(output_dim * 2, output_dim),
            initializer="he_normal",
            name="kernel",
            trainable=True,
        )

    def call(self, inputs):
        # 获取输入的正部分
        pos = ops.relu(inputs)
        # 获取输入的负部分
        neg = ops.relu(-inputs)
        # 连接正部分和负部分
        concatenated = ops.concatenate([pos, neg], axis=0)
        # 将连接的结果投影回与输入相同的维度
        return ops.matmul(concatenated, self.kernel)

现在，我们不是直接在一个端到端的模型中使用它，而是尝试在一些测试数据上调用这个层：

x = tf.random.normal(shape=(2, 5))
y = MyAntirectifier()(x)

我们得到以下错误：

...
      1 x = tf.random.normal(shape=(2, 5))
----> 2 y = MyAntirectifier()(x)
...
     17         neg = tf.nn.relu(-inputs)
     18         concatenated = tf.concat([pos, neg], axis=0)
---> 19         return tf.matmul(concatenated, self.kernel)
...
InvalidArgumentError: 矩阵大小不兼容: 输入[0]: [4,5], 输入[1]: [10,5] [操作:MatMul]

看起来我们的输入张量在 matmul 操作中的形状可能不正确。让我们添加一个打印语句来检查实际形状：

class MyAntirectifier(layers.Layer):
    def build(self, input_shape):
        output_dim = input_shape[-1]
        self.kernel = self.add_weight(
            shape=(output_dim * 2, output_dim),
            initializer="he_normal",
            name="kernel",
            trainable=True,
        )

    def call(self, inputs):
        pos = ops.relu(inputs)
        neg = ops.relu(-inputs)
        print("pos.shape:", pos.shape)
        print("neg.shape:", neg.shape)
        concatenated = ops.concatenate([pos, neg], axis=0)
        print("concatenated.shape:", concatenated.shape)
        print("kernel.shape:", self.kernel.shape)
        return ops.matmul(concatenated, self.kernel)

我们得到了以下输出：

pos.shape: (2, 5)
neg.shape: (2, 5)
concatenated.shape: (4, 5)
kernel.shape: (10, 5)

结果发现我们的 concat 操作使用了错误的轴！我们应该在特征轴 1 上连接 neg 和 pos，而不是在批处理轴 0 上。以下是正确的版本：

class MyAntirectifier(layers.Layer):
    def build(self, input_shape):
        output_dim = input_shape[-1]
        self.kernel = self.add_weight(
            shape=(output_dim * 2, output_dim),
            initializer="he_normal",
            name="kernel",
            trainable=True,
        )

    def call(self, inputs):
        pos = ops.relu(inputs)
        neg = ops.relu(-inputs)
        print("pos.shape:", pos.shape)
        print("neg.shape:", neg.shape)
        concatenated = ops.concatenate([pos, neg], axis=1)
        print("concatenated.shape:", concatenated.shape)
        print("kernel.shape:", self.kernel.shape)
        return ops.matmul(concatenated, self.kernel)

现在我们的代码运行良好：

x = keras.random.normal(shape=(2, 5))
y = MyAntirectifier()(x)

pos.shape: (2, 5)
neg.shape: (2, 5)
concatenated.shape: (2, 10)
kernel.shape: (10, 5)

提示 2：使用 `model.summary()` 和 `plot_model()` 来检查层输出形状

如果你正在处理复杂的网络拓扑，你需要一种方法来可视化你的层是如何连接的，以及它们如何变换通过它们的数据。

这是一个示例。考虑这个具有三个输入和两个输出的模型（摘自 Functional API guide）：

num_tags = 12  # 唯一问题标签的数量
num_words = 10000  # 预处理文本数据时获得的词汇表大小
num_departments = 4  # 用于预测的部门数量

title_input = keras.Input(
    shape=(None,), name="title"
)  # 可变长度的整数序列
body_input = keras.Input(shape=(None,), name="body")  # 可变长度的整数序列
tags_input = keras.Input(
    shape=(num_tags,), name="tags"
)  # 大小为 `num_tags` 的二进制向量

# 将标题中的每个单词嵌入到一个 64 维的向量中
title_features = layers.Embedding(num_words, 64)(title_input)
# 将文本中的每个单词嵌入到一个 64 维的向量中
body_features = layers.Embedding(num_words, 64)(body_input)

# 将标题中的嵌入单词序列减少为单个 128 维的向量
title_features = layers.LSTM(128)(title_features)
# 将正文中的嵌入单词序列减少为单个 32 维的向量
body_features = layers.LSTM(32)(body_features)

# 通过连接将所有可用特征合并为一个大的向量
x = layers.concatenate([title_features, body_features, tags_input])

# 在特征上方加一个逻辑回归进行优先级预测
priority_pred = layers.Dense(1, name="priority")(x)
# 在特征上方加一个部门分类器
department_pred = layers.Dense(num_departments, name="department")(x)

# 实例化一个端到端的模型，预测优先级和部门
model = keras.Model(
    inputs=[title_input, body_input, tags_input],
    outputs=[priority_pred, department_pred],
)

调用 summary() 可以帮助你检查每一层的输出形状：

model.summary()

模型: "functional_1"

┏━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━┓
┃ 层 (类型)         ┃ 输出形状      ┃ 参数 # ┃ 连接到         ┃
┡━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━┩
│ title (InputLayer)  │ (None, None)      │       0 │ -                    │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ body (InputLayer)   │ (None, None)      │       0 │ -                    │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ embedding           │ (None, None, 64)  │ 640,000 │ title[0][0]          │
│ (Embedding)         │                   │         │                      │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ embedding_1         │ (无, 无, 64)  │ 640,000 │ body[0][0]           │
│ (嵌入)         │                   │         │                      │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ lstm (长短期记忆)         │ (无, 128)       │  98,816 │ embedding[0][0]      │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ lstm_1 (长短期记忆)       │ (无, 32)        │  12,416 │ embedding_1[0][0]    │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ tags (输入层)   │ (无, 12)        │       0 │ -                    │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ concatenate         │ (无, 172)       │       0 │ lstm[0][0],          │
│ (拼接)       │                   │         │ lstm_1[0][0],        │
│                     │                   │         │ tags[0][0]           │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ priority (稠密层)    │ (无, 1)         │     173 │ concatenate[0][0]    │
├─────────────────────┼───────────────────┼─────────┼──────────────────────┤
│ department (稠密层)  │ (无, 4)         │     692 │ concatenate[0][0]    │
└─────────────────────┴───────────────────┴─────────┴──────────────────────┘

 总参数: 1,392,097 (5.31 MB)

 可训练参数: 1,392,097 (5.31 MB)

 非可训练参数: 0 (0.00 B)

您还可以使用 plot_model 可视化整个网络拓扑结构及输出形状:

keras.utils.plot_model(model, show_shapes=True)

png

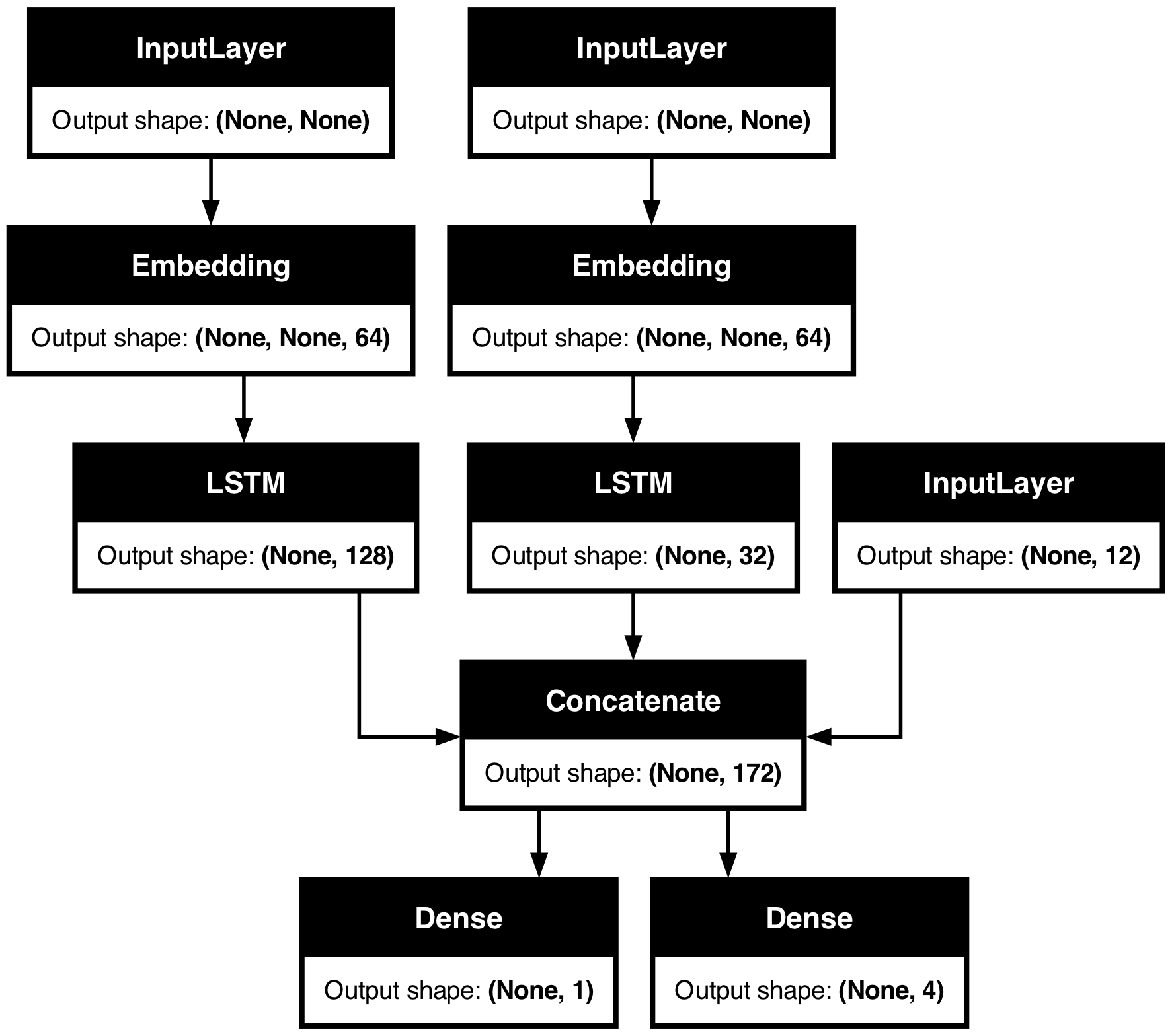
使用此图，任何连接级错误都会立即显而易见。

提示 3: 为了调试 `fit()` 期间发生的事情，使用 `run_eagerly=True`

fit() 方法运行得很快：它运行一个经过良好优化、完全编译的计算图。这对性能来说很棒，但这也意味着您执行的代码并不是您编写的 Python 代码。这在调试时可能会出现问题。正如您可能记得的，Python 运行缓慢——所以我们将其用作一个中间语言，而不是执行语言。

幸运的是，有一种简单的方法可以让您的代码在“调试模式”下完全渴望执行：将 run_eagerly=True 传递给 compile()。您的 fit() 调用现在将逐行执行，没有任何优化。这虽然较慢，但可以打印中间张量的值，或使用 Python 调试器。非常适合调试。

这是一个基本示例：让我们编写一个非常简单的模型，带有自定义的 train_step() 方法。我们的模型仅实现了梯度下降，但它使用一阶和二阶梯度的组合，而不是一阶梯度。到目前为止相当简单。

您能发现我们哪里做错了吗？

class MyModel(keras.Model):
    def train_step(self, data):
        inputs, targets = data
        trainable_vars = self.trainable_variables
        with tf.GradientTape() as tape2:
            with tf.GradientTape() as tape1:
                y_pred = self(inputs, training=True)  # 向前传播
                # 计算损失值
                # (损失函数在 `compile()` 中配置)
                loss = self.compute_loss(y=targets, y_pred=y_pred)
            # 计算一阶梯度
            dl_dw = tape1.gradient(loss, trainable_vars)
        # 计算二阶梯度
        d2l_dw2 = tape2.gradient(dl_dw, trainable_vars)

        # 组合一阶和二阶梯度
        grads = [0.5 * w1 + 0.5 * w2 for (w1, w2) in zip(d2l_dw2, dl_dw)]

        # 更新权重
        self.optimizer.apply_gradients(zip(grads, trainable_vars))

        # 更新指标（包括跟踪损失的指标）
        for metric in self.metrics:
            if metric.name == "loss":
                metric.update_state(loss)
            else:
                metric.update_state(targets, y_pred)

        # 返回一个字典，将指标名称映射到当前值
        return {m.name: m.result() for m in self.metrics}

让我们用这个自定义损失函数在 MNIST 上训练一个单层模型。

我们随机选择一个批量大小为 1024 和学习率为 0.1。总的想法是使用比通常更大的批量和学习率，因为我们的“改进”梯度应该使我们更快收敛。

# 构建 MyModel 的实例
def get_model():
    inputs = keras.Input(shape=(784,))
    intermediate = layers.Dense(256, activation="relu")(inputs)
    outputs = layers.Dense(10, activation="softmax")(intermediate)
    model = MyModel(inputs, outputs)
    return model


# 准备数据
(x_train, y_train), _ = keras.datasets.mnist.load_data()
x_train = np.reshape(x_train, (-1, 784)) / 255

model = get_model()
model.compile(
    optimizer=keras.optimizers.SGD(learning_rate=1e-2),
    loss="sparse_categorical_crossentropy",
)
model.fit(x_train, y_train, epochs=3, batch_size=1024, validation_split=0.1)

Epoch 1/3
 53/53 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 2.4264 - val_loss: 2.3036
Epoch 2/3
 53/53 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - loss: 2.3111 - val_loss: 2.3387
Epoch 3/3
 53/53 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 2.3442 - val_loss: 2.3697

<keras.src.callbacks.history.History at 0x29a899600>

哦，不，它没有收敛！某些事情并没有按计划进行。

是时候逐步打印我们梯度的运行情况了。

我们在 train_step 方法中添加了各种 print 语句，并确保将 run_eagerly=True 传递给 compile() 以逐步、渴望地运行我们的代码。

class MyModel(keras.Model):
    def train_step(self, data):
        print()
        print("----开始步骤: %d" % (self.step_counter,))
        self.step_counter += 1

        inputs, targets = data
        trainable_vars = self.trainable_variables
        with tf.GradientTape() as tape2:
            with tf.GradientTape() as tape1:
                y_pred = self(inputs, training=True)  # 正向传递
                # 计算损失值
                # (损失函数在`compile()`中配置)
                loss = self.compute_loss(y=targets, y_pred=y_pred)
            # 计算一阶梯度
            dl_dw = tape1.gradient(loss, trainable_vars)
        # 计算二阶梯度
        d2l_dw2 = tape2.gradient(dl_dw, trainable_vars)

        print("dl_dw[0]的最大值: %.4f" % tf.reduce_max(dl_dw[0]))
        print("dl_dw[0]的最小值: %.4f" % tf.reduce_min(dl_dw[0]))
        print("dl_dw[0]的均值: %.4f" % tf.reduce_mean(dl_dw[0]))
        print("-")
        print("d2l_dw2[0]的最大值: %.4f" % tf.reduce_max(d2l_dw2[0]))
        print("d2l_dw2[0]的最小值: %.4f" % tf.reduce_min(d2l_dw2[0]))
        print("d2l_dw2[0]的均值: %.4f" % tf.reduce_mean(d2l_dw2[0]))

        # 组合一阶和二阶梯度
        grads = [0.5 * w1 + 0.5 * w2 for (w1, w2) in zip(d2l_dw2, dl_dw)]

        # 更新权重
        self.optimizer.apply_gradients(zip(grads, trainable_vars))

        # 更新指标（包括跟踪损失的指标）
        for metric in self.metrics:
            if metric.name == "loss":
                metric.update_state(loss)
            else:
                metric.update_state(targets, y_pred)

        # 返回一个映射指标名称到当前值的字典
        return {m.name: m.result() for m in self.metrics}


model = get_model()
model.compile(
    optimizer=keras.optimizers.SGD(learning_rate=1e-2),
    loss="sparse_categorical_crossentropy",
    metrics=["sparse_categorical_accuracy"],
    run_eagerly=True,
)
model.step_counter = 0
# 我们传递epochs=1和steps_per_epoch=10来仅运行10个训练步骤。
model.fit(x_train, y_train, epochs=1, batch_size=1024, verbose=0, steps_per_epoch=10)

----开始步骤：0
dl_dw[0]的最大值：0.0332
dl_dw[0]的最小值：-0.0288
dl_dw[0]的均值：0.0003
-
d2l_dw2[0]的最大值：5.2691
d2l_dw2[0]的最小值：-2.6968
d2l_dw2[0]的均值：0.0981

----开始步骤：1
dl_dw[0]的最大值：0.0445
dl_dw[0]的最小值：-0.0169
dl_dw[0]的均值：0.0013
-
d2l_dw2[0]的最大值：3.3575
d2l_dw2[0]的最小值：-1.9024
d2l_dw2[0]的均值：0.0726

----开始步骤：2
dl_dw[0]的最大值：0.0669
dl_dw[0]的最小值：-0.0153
dl_dw[0]的均值：0.0013
-
d2l_dw2[0]的最大值：5.0661
d2l_dw2[0]的最小值：-1.7168
d2l_dw2[0]的均值：0.0809

----开始步骤：3
dl_dw[0]的最大值：0.0545
dl_dw[0]的最小值：-0.0125
dl_dw[0]的均值：0.0008
-
d2l_dw2[0]的最大值：6.5223
d2l_dw2[0]的最小值：-0.6604
d2l_dw2[0]的均值：0.0991

----开始步骤：4
dl_dw[0]的最大值：0.0247
dl_dw[0]的最小值：-0.0152
dl_dw[0]的均值：-0.0001
-
d2l_dw2[0]的最大值：2.8030
d2l_dw2[0]的最小值：-0.1156
d2l_dw2[0]的均值：0.0321

----开始步骤：5
dl_dw[0]的最大值：0.0051
dl_dw[0]的最小值：-0.0096
dl_dw[0]的均值：-0.0001
-
d2l_dw2[0]的最大值：0.2545
d2l_dw2[0]的最小值：-0.0284
d2l_dw2[0]的均值：0.0079

----开始步骤：6
dl_dw[0]的最大值：0.0041
dl_dw[0]的最小值：-0.0102
dl_dw[0]的均值：-0.0001
-
d2l_dw2[0]的最大值：0.2198
d2l_dw2[0]的最小值：-0.0175
d2l_dw2[0]的均值：0.0069

----开始步骤：7
dl_dw[0]的最大值：0.0035
dl_dw[0]的最小值：-0.0086
dl_dw[0]的均值：-0.0001
-
d2l_dw2[0]的最大值：0.1485
d2l_dw2[0]的最小值：-0.0175
d2l_dw2[0]的均值：0.0060

----开始步骤：8
dl_dw[0]的最大值：0.0039
dl_dw[0]的最小值：-0.0094
dl_dw[0]的均值：-0.0001
-
d2l_dw2[0]的最大值：0.1454
d2l_dw2[0]的最小值：-0.0130
d2l_dw2[0]的均值：0.0061

----开始步骤：9
dl_dw[0]的最大值：0.0028
dl_dw[0]的最小值：-0.0087
dl_dw[0]的均值：-0.0001
-
d2l_dw2[0]的最大值：0.1491
d2l_dw2[0]的最小值：-0.0326
d2l_dw2[0]的均值：0.0058

<keras.src.callbacks.history.History at 0x2a0d1e440>

我们学到了什么？

一阶和二阶梯度的值可能相差几个数量级。
有时，它们甚至可能没有相同的符号。
它们的值在每一步中可能会有很大的变化。

这让我们产生了一个显而易见的想法：在组合它们之前，让我们对梯度进行归一化。

class MyModel(keras.Model):
    def train_step(self, data):
        inputs, targets = data
        trainable_vars = self.trainable_variables
        with tf.GradientTape() as tape2:
            with tf.GradientTape() as tape1:
                y_pred = self(inputs, training=True)  # 前向传递
                # 计算损失值
                # （损失函数在`compile()`中配置）
                loss = self.compute_loss(y=targets, y_pred=y_pred)
            # 计算一阶梯度
            dl_dw = tape1.gradient(loss, trainable_vars)
        # 计算二阶梯度
        d2l_dw2 = tape2.gradient(dl_dw, trainable_vars)

        dl_dw = [tf.math.l2_normalize(w) for w in dl_dw]
        d2l_dw2 = [tf.math.l2_normalize(w) for w in d2l_dw2]

        # 组合一阶和二阶梯度
        grads = [0.5 * w1 + 0.5 * w2 for (w1, w2) in zip(d2l_dw2, dl_dw)]

        # 更新权重
        self.optimizer.apply_gradients(zip(grads, trainable_vars))

        # 更新指标（包含跟踪损失的指标）
        for metric in self.metrics:
            if metric.name == "loss":
                metric.update_state(loss)
            else:
                metric.update_state(targets, y_pred)

        # 返回一个字典，将指标名称映射到当前值
        return {m.name: m.result() for m in self.metrics}


model = get_model()
model.compile(
    optimizer=keras.optimizers.SGD(learning_rate=1e-2),
    loss="sparse_categorical_crossentropy",
    metrics=["sparse_categorical_accuracy"],
)
model.fit(x_train, y_train, epochs=5, batch_size=1024, validation_split=0.1)

Epoch 1/5
 53/53 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - 稀疏类别准确率: 0.1250 - 损失: 2.3185 - 验证损失: 2.0502 - 验证稀疏类别准确率: 0.3373
Epoch 2/5
 53/53 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - 稀疏类别准确率: 0.3966 - 损失: 1.9934 - 验证损失: 1.8032 - 验证稀疏类别准确率: 0.5698
Epoch 3/5
 53/53 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - 稀疏类别准确率: 0.5663 - 损失: 1.7784 - 验证损失: 1.6241 - 验证稀疏类别准确率: 0.6470
Epoch 4/5
 53/53 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - 稀疏类别准确率: 0.6135 - 损失: 1.6256 - 验证损失: 1.5010 - 验证稀疏类别准确率: 0.6595
Epoch 5/5
 53/53 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - 稀疏类别准确率: 0.6216 - 损失: 1.5173 - 验证损失: 1.4169 - 验证稀疏类别准确率: 0.6625

<keras.src.callbacks.history.History at 0x2a0d4c640>

现在，训练收敛了！它的表现并不好，但至少模型学到了一些东西。

经过几分钟的参数调整，我们得到了以下配置，效果还算不错（达到了97%的验证准确率，并且似乎在过拟合方面相对稳健）：

使用 0.2 * w1 + 0.8 * w2 来组合梯度。
使用一个随时间线性衰减的学习率。

我不会说这个想法是有效的——这并不是你应该采用的二阶优化方法（提示：请参阅牛顿法和高斯-牛顿法、拟牛顿方法和BFGS）。但希望这个演示能给你一个思路，告诉你如何调试困难的训练情况。

记住：在调试 fit() 中发生的事情时使用 run_eagerly=True。当你的代码最终按预期工作时，请确保删除此标志，以获取最佳的运行时性能！

这是我们的最终训练过程：

class MyModel(keras.Model):
    def train_step(self, data):
        inputs, targets = data
        trainable_vars = self.trainable_variables
        with tf.GradientTape() as tape2:
            with tf.GradientTape() as tape1:
                y_pred = self(inputs, training=True)  # 前向传播
                # 计算损失值
                # （损失函数在 `compile()` 中配置）
                loss = self.compute_loss(y=targets, y_pred=y_pred)
            # 计算一阶梯度
            dl_dw = tape1.gradient(loss, trainable_vars)
        # 计算二阶梯度
        d2l_dw2 = tape2.gradient(dl_dw, trainable_vars)

        dl_dw = [tf.math.l2_normalize(w) for w in dl_dw]
        d2l_dw2 = [tf.math.l2_normalize(w) for w in d2l_dw2]

        # 组合一阶和二阶梯度
        grads = [0.2 * w1 + 0.8 * w2 for (w1, w2) in zip(d2l_dw2, dl_dw)]

        # 更新权重
        self.optimizer.apply_gradients(zip(grads, trainable_vars))

        # 更新指标（包括跟踪损失的指标）
        for metric in self.metrics:
            if metric.name == "loss":
                metric.update_state(loss)
            else:
                metric.update_state(targets, y_pred)

        # 返回一个字典，将指标名称映射到当前值
        return {m.name: m.result() for m in self.metrics}


model = get_model()
lr = learning_rate = keras.optimizers.schedules.InverseTimeDecay(
    initial_learning_rate=0.1, decay_steps=25, decay_rate=0.1
)
model.compile(
    optimizer=keras.optimizers.SGD(lr),
    loss="sparse_categorical_crossentropy",
    metrics=["sparse_categorical_accuracy"],
)
model.fit(x_train, y_train, epochs=50, batch_size=2048, validation_split=0.1)

Epoch 1/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 1s 14ms/step - sparse_categorical_accuracy: 0.5056 - loss: 1.7508 - val_loss: 0.6378 - val_sparse_categorical_accuracy: 0.8658
Epoch 2/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - sparse_categorical_accuracy: 0.8407 - loss: 0.6323 - val_loss: 0.4039 - val_sparse_categorical_accuracy: 0.8970
Epoch 3/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - sparse_categorical_accuracy: 0.8807 - loss: 0.4472 - val_loss: 0.3243 - val_sparse_categorical_accuracy: 0.9120
Epoch 4/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - sparse_categorical_accuracy: 0.8947 - loss: 0.3781 - val_loss: 0.2861 - val_sparse_categorical_accuracy: 0.9235
Epoch 5/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9022 - loss: 0.3453 - val_loss: 0.2622 - val_sparse_categorical_accuracy: 0.9288
Epoch 6/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9093 - loss: 0.3243 - val_loss: 0.2523 - val_sparse_categorical_accuracy: 0.9303
Epoch 7/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9148 - loss: 0.3021 - val_loss: 0.2362 - val_sparse_categorical_accuracy: 0.9338
Epoch 8/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9184 - loss: 0.2899 - val_loss: 0.2289 - val_sparse_categorical_accuracy: 0.9365
Epoch 9/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9212 - loss: 0.2784 - val_loss: 0.2183 - val_sparse_categorical_accuracy: 0.9383
Epoch 10/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9246 - loss: 0.2670 - val_loss: 0.2097 - val_sparse_categorical_accuracy: 0.9405
Epoch 11/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9267 - loss: 0.2563 - val_loss: 0.2063 - val_sparse_categorical_accuracy: 0.9442
Epoch 12/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9313 - loss: 0.2412 - val_loss: 0.1965 - val_sparse_categorical_accuracy: 0.9458
Epoch 13/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9324 - loss: 0.2411 - val_loss: 0.1917 - val_sparse_categorical_accuracy: 0.9472
Epoch 14/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9359 - loss: 0.2260 - val_loss: 0.1861 - val_sparse_categorical_accuracy: 0.9495
Epoch 15/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9374 - loss: 0.2234 - val_loss: 0.1804 - val_sparse_categorical_accuracy: 0.9517
Epoch 16/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 14ms/step - sparse_categorical_accuracy: 0.9382 - loss: 0.2196 - val_loss: 0.1761 - val_sparse_categorical_accuracy: 0.9528
Epoch 17/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 14ms/step - sparse_categorical_accuracy: 0.9417 - loss: 0.2076 - val_loss: 0.1709 - val_sparse_categorical_accuracy: 0.9557
Epoch 18/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step - sparse_categorical_accuracy: 0.9423 - loss: 0.2032 - val_loss: 0.1664 - val_sparse_categorical_accuracy: 0.9555
Epoch 19/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9444 - loss: 0.1953 - val_loss: 0.1616 - val_sparse_categorical_accuracy: 0.9582
Epoch 20/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9451 - loss: 0.1916 - val_loss: 0.1597 - val_sparse_categorical_accuracy: 0.9592
Epoch 21/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step - sparse_categorical_accuracy: 0.9473 - loss: 0.1866 - val_loss: 0.1563 - val_sparse_categorical_accuracy: 0.9615
Epoch 22/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9486 - loss: 0.1818 - val_loss: 0.1520 - val_sparse_categorical_accuracy: 0.9617
Epoch 23/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9502 - loss: 0.1794 - val_loss: 0.1499 - val_sparse_categorical_accuracy: 0.9635
Epoch 24/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9502 - loss: 0.1759 - val_loss: 0.1466 - val_sparse_categorical_accuracy: 0.9640
Epoch 25/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9515 - loss: 0.1714 - val_loss: 0.1437 - val_sparse_categorical_accuracy: 0.9645
Epoch 26/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 14ms/step - sparse_categorical_accuracy: 0.9535 - loss: 0.1649 - val_loss: 0.1435 - val_sparse_categorical_accuracy: 0.9640
Epoch 27/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step - sparse_categorical_accuracy: 0.9548 - loss: 0.1628 - val_loss: 0.1411 - val_sparse_categorical_accuracy: 0.9650
Epoch 28/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9541 - loss: 0.1620 - val_loss: 0.1384 - val_sparse_categorical_accuracy: 0.9655
Epoch 29/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9564 - loss: 0.1560 - val_loss: 0.1359 - val_sparse_categorical_accuracy: 0.9668
Epoch 30/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9577 - loss: 0.1547 - val_loss: 0.1338 - val_sparse_categorical_accuracy: 0.9672
Epoch 31/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9569 - loss: 0.1520 - val_loss: 0.1329 - val_sparse_categorical_accuracy: 0.9663
Epoch 32/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9582 - loss: 0.1478 - val_loss: 0.1320 - val_sparse_categorical_accuracy: 0.9675
Epoch 33/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9582 - loss: 0.1483 - val_loss: 0.1292 - val_sparse_categorical_accuracy: 0.9670
Epoch 34/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9594 - loss: 0.1448 - val_loss: 0.1274 - val_sparse_categorical_accuracy: 0.9677
Epoch 35/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9587 - loss: 0.1452 - val_loss: 0.1262 - val_sparse_categorical_accuracy: 0.9678
Epoch 36/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9603 - loss: 0.1418 - val_loss: 0.1251 - val_sparse_categorical_accuracy: 0.9677
Epoch 37/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9603 - loss: 0.1402 - val_loss: 0.1238 - val_sparse_categorical_accuracy: 0.9682
Epoch 38/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9618 - loss: 0.1382 - val_loss: 0.1228 - val_sparse_categorical_accuracy: 0.9680
Epoch 39/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9630 - loss: 0.1335 - val_loss: 0.1213 - val_sparse_categorical_accuracy: 0.9695
Epoch 40/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9629 - loss: 0.1327 - val_loss: 0.1198 - val_sparse_categorical_accuracy: 0.9698
Epoch 41/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9639 - loss: 0.1323 - val_loss: 0.1191 - val_sparse_categorical_accuracy: 0.9695
Epoch 42/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9629 - loss: 0.1346 - val_loss: 0.1183 - val_sparse_categorical_accuracy: 0.9692
Epoch 43/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9661 - loss: 0.1262 - val_loss: 0.1182 - val_sparse_categorical_accuracy: 0.9700
Epoch 44/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9652 - loss: 0.1274 - val_loss: 0.1163 - val_sparse_categorical_accuracy: 0.9702
Epoch 45/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9650 - loss: 0.1259 - val_loss: 0.1154 - val_sparse_categorical_accuracy: 0.9708
Epoch 46/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - sparse_categorical_accuracy: 0.9647 - loss: 0.1246 - val_loss: 0.1148 - val_sparse_categorical_accuracy: 0.9703
Epoch 47/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9659 - loss: 0.1236 - val_loss: 0.1137 - val_sparse_categorical_accuracy: 0.9707
Epoch 48/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9665 - loss: 0.1221 - val_loss: 0.1133 - val_sparse_categorical_accuracy: 0.9710
Epoch 49/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9675 - loss: 0.1192 - val_loss: 0.1124 - val_sparse_categorical_accuracy: 0.9712
Epoch 50/50
 27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step - sparse_categorical_accuracy: 0.9664 - loss: 0.1214 - val_loss: 0.1112 - val_sparse_categorical_accuracy: 0.9707

<keras.src.callbacks.history.History at 0x29e76ae60>

Keras 调试技巧

◆ 介绍

◆ 技巧 1: 在测试整个模型之前先测试每个部分

◆ 提示 2：使用 model.summary() 和 plot_model() 来检查层输出形状

◆ 提示 3: 为了调试 fit() 期间发生的事情，使用 run_eagerly=True

Keras 调试技巧

介绍

技巧 1: 在测试整个模型之前先测试每个部分

提示 2：使用 model.summary() 和 plot_model() 来检查层输出形状

提示 3: 为了调试 fit() 期间发生的事情，使用 run_eagerly=True

提示 2：使用 `model.summary()` 和 `plot_model()` 来检查层输出形状

提示 3: 为了调试 `fit()` 期间发生的事情，使用 `run_eagerly=True`