估算模型训练所需的样本大小
作者: JacoVerster
创建日期: 2021/05/20
最后修改日期: 2021/06/06
描述: 建模训练集大小与模型准确性之间的关系。
介绍
在许多现实场景中,可用来训练深度学习模型的图像数据量是有限的。这在医学成像领域尤其如此,因为数据集创建的成本很高。通常在接触一个新问题时,第一个问题是:“我们需要多少张图像才能训练出一个足够好的机器学习模型?”
在大多数情况下,只有一小部分样本可用,我们可以利用它来建模训练数据大小与模型性能之间的关系。这种模型可以用于估算达到所需模型性能所需的最佳图像数量,以确定样本大小。
Balki 等人对样本大小确定方法的系统评审提供了几种样本大小确定方法的示例。在这个例子中,使用了一种平衡子抽样方案来确定我们模型的最佳样本大小。这是通过选择一个包含 Y 张图像的随机子样本并使用该子样本训练模型来完成的。然后在独立的测试集上评估模型。对于每个子样本,此过程重复 N 次,以允许构建观察到的性能的均值和置信区间。
设置
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import keras
from keras import layers
import tensorflow_datasets as tfds
# 定义种子和固定变量
seed = 42
keras.utils.set_random_seed(seed)
AUTO = tf.data.AUTOTUNE
加载 TensorFlow 数据集并转换为 NumPy 数组
我们将使用 TF Flowers 数据集。
# 指定数据集参数
dataset_name = "tf_flowers"
batch_size = 64
image_size = (224, 224)
# 从 tfds 加载数据并分割 10% 用作测试集
(train_data, test_data), ds_info = tfds.load(
dataset_name,
split=["train[:90%]", "train[90%:]"],
shuffle_files=True,
as_supervised=True,
with_info=True,
)
# 提取类的数量和类名列表
num_classes = ds_info.features["label"].num_classes
class_names = ds_info.features["label"].names
print(f"类的数量: {num_classes}")
print(f"类名: {class_names}")
# 将数据集转换为 NumPy 数组
def dataset_to_array(dataset, image_size, num_classes):
images, labels = [], []
for img, lab in dataset.as_numpy_iterator():
images.append(tf.image.resize(img, image_size).numpy())
labels.append(tf.one_hot(lab, num_classes))
return np.array(images), np.array(labels)
img_train, label_train = dataset_to_array(train_data, image_size, num_classes)
img_test, label_test = dataset_to_array(test_data, image_size, num_classes)
num_train_samples = len(img_train)
print(f"训练样本数量: {num_train_samples}")
类的数量: 5
类名: ['蒲公英', '雏菊', '郁金香', '向日葵', '玫瑰']
训练样本数量: 3303
绘制测试集的一些示例
plt.figure(figsize=(16, 12))
for n in range(30):
ax = plt.subplot(5, 6, n + 1)
plt.imshow(img_test[n].astype("uint8"))
plt.title(np.array(class_names)[label_test[n] == True][0])
plt.axis("off")

数据增强
定义图像增强使用 keras 预处理层,并将其应用于训练集。
# 定义图像增强模型
image_augmentation = keras.Sequential(
[
layers.RandomFlip(mode="horizontal"),
layers.RandomRotation(factor=0.1),
layers.RandomZoom(height_factor=(-0.1, -0)),
layers.RandomContrast(factor=0.1),
],
)
# 将增强应用于训练图像并绘制一些示例
img_train = image_augmentation(img_train).numpy()
plt.figure(figsize=(16, 12))
for n in range(30):
ax = plt.subplot(5, 6, n + 1)
plt.imshow(img_train[n].astype("uint8"))
plt.title(np.array(class_names)[label_train[n] == True][0])
plt.axis("off")

定义模型构建和训练函数
我们创建了一些方便的函数来构建一个迁移学习模型,编译并训练它,并解冻层以进行微调。
def build_model(num_classes, img_size=image_size[0], top_dropout=0.3):
"""基于预训练的 MobileNetV2 创建一个分类器。
参数:
num_classes: 整数,softmax 层中使用的类别数量。
img_size: 整数,输入图像的正方形大小(默认值为 224)。
top_dropout: 整数,dropout 层的值(默认值为 0.3)。
返回:
未编译的 Keras 模型。
"""
# 创建 MobileNetV2 的输入和预处理层
inputs = layers.Input(shape=(img_size, img_size, 3))
x = layers.Rescaling(scale=1.0 / 127.5, offset=-1)(inputs)
model = keras.applications.MobileNetV2(
include_top=False, weights="imagenet", input_tensor=x
)
# 冻结预训练权重
model.trainable = False
# 重建顶部
x = layers.GlobalAveragePooling2D(name="avg_pool")(model.output)
x = layers.Dropout(top_dropout)(x)
outputs = layers.Dense(num_classes, activation="softmax")(x)
model = keras.Model(inputs, outputs)
print("可训练权重:", len(model.trainable_weights))
print("不可训练权重:", len(model.non_trainable_weights))
return model
def compile_and_train(
model,
training_data,
training_labels,
metrics=[keras.metrics.AUC(name="auc"), "acc"],
optimizer=keras.optimizers.Adam(),
patience=5,
epochs=5,
):
"""编译并训练模型。
参数:
model: 未编译的 Keras 模型。
training_data: NumPy 数组,训练数据。
training_labels: NumPy 数组,训练标签。
metrics: Keras/TF 指标,至少需要 'auc' 指标(默认是
`[keras.metrics.AUC(name='auc'), 'acc']`)。
optimizer: Keras/TF 优化器(默认是 `keras.optimizers.Adam()`)。
patience: 整数,EarlyStopping 的耐心轮数(默认值为 5)。
epochs: 整数,训练的轮数(默认值为 5)。
返回:
训练的 Keras 模型的训练历史。
"""
stopper = keras.callbacks.EarlyStopping(
monitor="val_auc",
mode="max",
min_delta=0,
patience=patience,
verbose=1,
restore_best_weights=True,
)
model.compile(loss="categorical_crossentropy", optimizer=optimizer, metrics=metrics)
history = model.fit(
x=training_data,
y=training_labels,
batch_size=batch_size,
epochs=epochs,
validation_split=0.1,
callbacks=[stopper],
)
return history
def unfreeze(model, block_name, verbose=0):
"""解冻 Keras 模型层。
参数:
model: Keras 模型。
block_name: 字符串,层名称,例如 block_name = 'block4'。
检查提供的字符串是否在层名称中。
verbose: 整数,0 表示静默,1 打印出层的可训练状态。
返回:
Keras 模型,所有在指定的 block_name 之后(包括该层)的层可训练,排除 BatchNormalization 层。
"""
# 从 block_name 开始解冻
set_trainable = False
for layer in model.layers:
if block_name in layer.name:
set_trainable = True
if set_trainable and not isinstance(layer, layers.BatchNormalization):
layer.trainable = True
if verbose == 1:
print(layer.name, "可训练")
else:
if verbose == 1:
print(layer.name, "不可训练")
print("可训练权重:", len(model.trainable_weights))
print("不可训练权重:", len(model.non_trainable_weights))
return model
定义迭代训练函数
为了对多个子样本集训练模型,我们需要创建一个迭代训练函数。
def train_model(training_data, training_labels):
"""训练模型如下:
- 仅训练顶部层10个周期。
- 解冻更深层。
- 再训练20个周期。
参数:
training_data: NumPy数组,训练数据。
training_labels: NumPy数组,训练标签。
返回:
模型精度。
"""
model = build_model(num_classes)
# 编译并训练顶部层
history = compile_and_train(
model,
training_data,
training_labels,
metrics=[keras.metrics.AUC(name="auc"), "acc"],
optimizer=keras.optimizers.Adam(),
patience=3,
epochs=10,
)
# 从第10块开始解冻模型
model = unfreeze(model, "block_10")
# 用较低的学习率编译并训练20个周期
fine_tune_epochs = 20
total_epochs = history.epoch[-1] + fine_tune_epochs
history_fine = compile_and_train(
model,
training_data,
training_labels,
metrics=[keras.metrics.AUC(name="auc"), "acc"],
optimizer=keras.optimizers.Adam(learning_rate=1e-4),
patience=5,
epochs=total_epochs,
)
# 计算模型在测试集上的精度
_, _, acc = model.evaluate(img_test, label_test)
return np.round(acc, 4)
迭代训练模型
现在我们有了模型构建函数和支持迭代的函数,我们可以在多个子样本分割上训练模型。
- 我们选择子样本分割为下载数据集的5%、10%、25%和50%。我们假装当前只有50%的实际数据可用。
- 我们在每个分割上从头开始训练模型5次,并记录准确性值。
请注意,这将训练20个模型,并需要一些时间。确保您有一个GPU运行时处于活动状态。
为了保持此示例轻量化,提供了来自上次训练运行的样本数据。
def train_iteratively(sample_splits=[0.05, 0.1, 0.25, 0.5], iter_per_split=5):
"""针对多个样本分割迭代训练模型。
参数:
sample_splits: 列表/Numpy数组,包含训练集中用于训练的比例。
iter_per_split: 整数,每个样本分割重复训练模型的次数。
返回:
所有分割和迭代的训练准确性及每个分割用于训练的样本数量。
"""
# 训练所有样本模型并计算准确性
train_acc = []
sample_sizes = []
for fraction in sample_splits:
print(f"分割比例: {fraction}")
# 对于每个样本大小重复训练3次
sample_accuracy = []
num_samples = int(num_train_samples * fraction)
for i in range(iter_per_split):
print(f"第 {i+1} 次运行,共 {iter_per_split} 次:")
# 创建部分子集
rand_idx = np.random.randint(num_train_samples, size=num_samples)
train_img_subset = img_train[rand_idx, :]
train_label_subset = label_train[rand_idx, :]
# 训练模型并计算准确性
accuracy = train_model(train_img_subset, train_label_subset)
print(f"准确性: {accuracy}")
sample_accuracy.append(accuracy)
train_acc.append(sample_accuracy)
sample_sizes.append(num_samples)
return train_acc, sample_sizes
# 运行上述函数生成以下输出
train_acc = [
[0.8202, 0.7466, 0.8011, 0.8447, 0.8229],
[0.861, 0.8774, 0.8501, 0.8937, 0.891],
[0.891, 0.9237, 0.8856, 0.9101, 0.891],
[0.8937, 0.9373, 0.9128, 0.8719, 0.9128],
]
sample_sizes = [165, 330, 825, 1651]
学习曲线
我们现在通过将指数曲线拟合到平均准确性点来绘制学习曲线。我们使用TF来拟合一条指数函数。
然后我们推断学习曲线以预测在整个训练集上训练的模型的准确性。
def fit_and_predict(train_acc, sample_sizes, pred_sample_size):
"""拟合学习曲线以模型训练准确度结果。
参数:
train_acc: 列表/Numpy 数组,所有模型
训练拆分和迭代的训练准确度。
sample_sizes: 列表/Numpy 数组,每个拆分用于训练的样本数量。
pred_sample_size: 整数,基于
拟合学习曲线预测模型准确度的样本大小。
"""
x = sample_sizes
mean_acc = tf.convert_to_tensor([np.mean(i) for i in train_acc])
error = [np.std(i) for i in train_acc]
# 定义均方误差成本和指数曲线拟合函数
mse = keras.losses.MeanSquaredError()
def exp_func(x, a, b):
return a * x**b
# 定义变量、学习率和用于拟合的训练轮数
a = tf.Variable(0.0)
b = tf.Variable(0.0)
learning_rate = 0.01
training_epochs = 5000
# 将指数函数拟合到数据
for epoch in range(training_epochs):
with tf.GradientTape() as tape:
y_pred = exp_func(x, a, b)
cost_function = mse(y_pred, mean_acc)
# 获取梯度并计算调整后的权重
gradients = tape.gradient(cost_function, [a, b])
a.assign_sub(gradients[0] * learning_rate)
b.assign_sub(gradients[1] * learning_rate)
print(f"曲线拟合权重: a = {a.numpy()} 和 b = {b.numpy()}.")
# 现在我们可以估算 pred_sample_size 的准确度
max_acc = exp_func(pred_sample_size, a, b).numpy()
# 打印预测的 x 值并附加到图值
print(f"预计在 {pred_sample_size} 个样本中模型准确度为 {max_acc}。")
x_cont = np.linspace(x[0], pred_sample_size, 100)
# 构建图形
fig, ax = plt.subplots(figsize=(12, 6))
ax.errorbar(x, mean_acc, yerr=error, fmt="o", label="均值准确度和标准差。")
ax.plot(x_cont, exp_func(x_cont, a, b), "r-", label="拟合的指数曲线。")
ax.set_ylabel("模型分类准确度。", fontsize=12)
ax.set_xlabel("训练样本大小。", fontsize=12)
ax.set_xticks(np.append(x, pred_sample_size))
ax.set_yticks(np.append(mean_acc, max_acc))
ax.set_xticklabels(list(np.append(x, pred_sample_size)), rotation=90, fontsize=10)
ax.yaxis.set_tick_params(labelsize=10)
ax.set_title("学习曲线:模型准确度与样本大小。", fontsize=14)
ax.legend(loc=(0.75, 0.75), fontsize=10)
ax.xaxis.grid(True)
ax.yaxis.grid(True)
plt.tight_layout()
plt.show()
# 计算曲线拟合的平均绝对误差(MAE),以查看拟合数据的效果。
# 误差越小,拟合效果越好。
mae = keras.losses.MeanAbsoluteError()
print(f"曲线拟合的 mae 为 {mae(mean_acc, exp_func(x, a, b)).numpy()}。")
# 我们使用整个训练集来预测模型准确度
fit_and_predict(train_acc, sample_sizes, pred_sample_size=num_train_samples)
曲线拟合权重: a = 0.6445642113685608 和 b = 0.048097413033246994.
对于3303个样本,预测的模型准确度为0.9517362117767334。
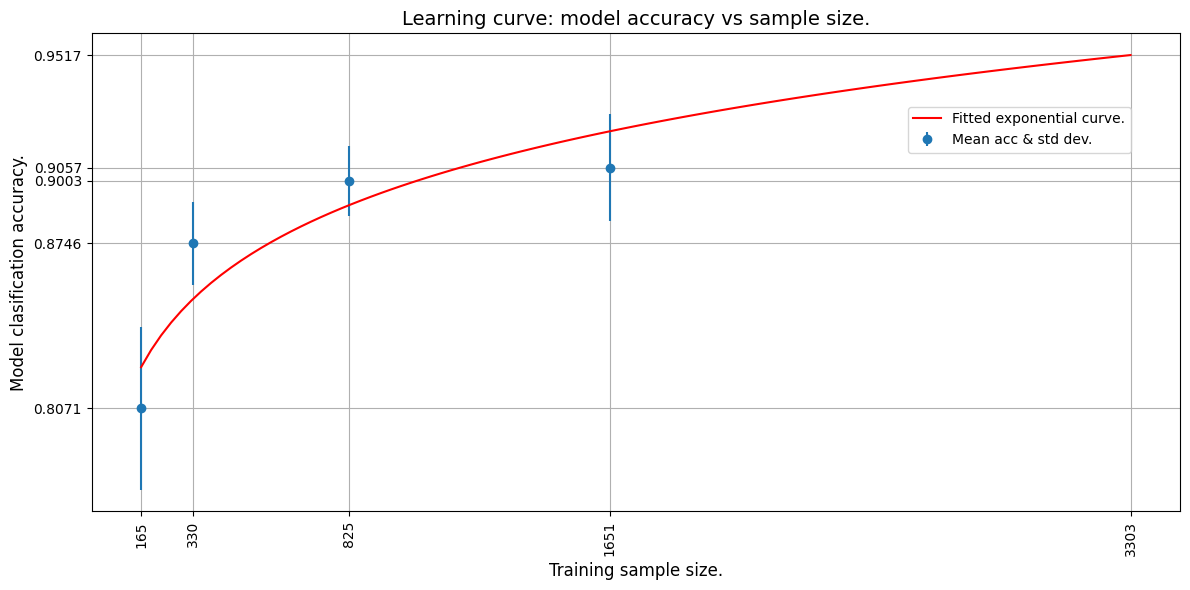
曲线拟合的mae为0.016098767518997192。
从外推的曲线中我们可以看到,3303张图像将产生估计的准确率约为95%。
现在,让我们使用所有数据(3303张图像)来训练模型,看看我们的预测是否准确!
# 现在用完整数据集训练模型以获得实际准确度
accuracy = train_model(img_train, label_train)
print(f"在{num_train_samples}张图像上达到的模型准确度为{accuracy}!")
/var/folders/8n/8w8cqnvj01xd4ghznl11nyn000_93_/T/ipykernel_30919/1838736464.py:16: UserWarning: `input_shape` 未定义或不是正方形,或者 `rows` 不在 [96, 128, 160, 192, 224] 中。输入形状 (224, 224) 的权重将作为默认值加载。
model = keras.applications.MobileNetV2(
可训练权重: 2
不可训练权重: 260
第 1 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 18s 338ms/step - acc: 0.4305 - auc: 0.7221 - loss: 1.4585 - val_acc: 0.8218 - val_auc: 0.9700 - val_loss: 0.5043
第 2 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 15s 326ms/step - acc: 0.7666 - auc: 0.9504 - loss: 0.6287 - val_acc: 0.8792 - val_auc: 0.9838 - val_loss: 0.3733
第 3 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 332ms/step - acc: 0.8252 - auc: 0.9673 - loss: 0.5039 - val_acc: 0.8852 - val_auc: 0.9880 - val_loss: 0.3182
第 4 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 348ms/step - acc: 0.8458 - auc: 0.9768 - loss: 0.4264 - val_acc: 0.8822 - val_auc: 0.9893 - val_loss: 0.2956
第 5 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 350ms/step - acc: 0.8661 - auc: 0.9812 - loss: 0.3821 - val_acc: 0.8912 - val_auc: 0.9903 - val_loss: 0.2755
第 6 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 336ms/step - acc: 0.8656 - auc: 0.9836 - loss: 0.3555 - val_acc: 0.9003 - val_auc: 0.9906 - val_loss: 0.2701
第 7 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 331ms/step - acc: 0.8800 - auc: 0.9846 - loss: 0.3430 - val_acc: 0.8943 - val_auc: 0.9914 - val_loss: 0.2548
第 8 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 333ms/step - acc: 0.8917 - auc: 0.9871 - loss: 0.3143 - val_acc: 0.8973 - val_auc: 0.9917 - val_loss: 0.2494
第 9 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 15s 320ms/step - acc: 0.9003 - auc: 0.9891 - loss: 0.2906 - val_acc: 0.9063 - val_auc: 0.9908 - val_loss: 0.2463
第 10 轮/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 15s 324ms/step - acc: 0.8997 - auc: 0.9895 - loss: 0.2839 - val_acc: 0.9124 - val_auc: 0.9912 - val_loss: 0.2394
可训练权重: 24
不可训练权重: 238
第 1 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 27s 537ms/step - acc: 0.8457 - auc: 0.9747 - loss: 0.4365 - val_acc: 0.9094 - val_auc: 0.9916 - val_loss: 0.2692
第 2 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 24s 502ms/step - acc: 0.9223 - auc: 0.9932 - loss: 0.2198 - val_acc: 0.9033 - val_auc: 0.9891 - val_loss: 0.2826
第 3 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 534ms/step - acc: 0.9499 - auc: 0.9972 - loss: 0.1399 - val_acc: 0.9003 - val_auc: 0.9910 - val_loss: 0.2804
第 4 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 26s 554ms/step - acc: 0.9590 - auc: 0.9983 - loss: 0.1130 - val_acc: 0.9396 - val_auc: 0.9968 - val_loss: 0.1510
第 5 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 533ms/step - acc: 0.9805 - auc: 0.9996 - loss: 0.0538 - val_acc: 0.9486 - val_auc: 0.9914 - val_loss: 0.1795
第 6 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 24s 516ms/step - acc: 0.9949 - auc: 1.0000 - loss: 0.0226 - val_acc: 0.9124 - val_auc: 0.9833 - val_loss: 0.3186
第 7 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 534ms/step - acc: 0.9900 - auc: 0.9999 - loss: 0.0297 - val_acc: 0.9275 - val_auc: 0.9881 - val_loss: 0.3017
第 8 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 536ms/step - acc: 0.9910 - auc: 0.9999 - loss: 0.0228 - val_acc: 0.9426 - val_auc: 0.9927 - val_loss: 0.1938
第 9 轮/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 0s 489ms/step - acc: 0.9995 - auc: 1.0000 - loss: 0.0069恢复模型权重,使之从最佳轮次的末尾恢复: 4。
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 527ms/step - acc: 0.9995 - auc: 1.0000 - loss: 0.0068 - val_acc: 0.9426 - val_auc: 0.9919 - val_loss: 0.2957
第 9 轮: 早停
12/12 ━━━━━━━━━━━━━━━━━━━━ 2s 170ms/step - acc: 0.9641 - auc: 0.9972 - loss: 0.1264
在3303张图像上达到的模型准确度为0.9964!
结论
我们看到使用3303张图像达到了大约94-96%*的模型准确度。这与我们的估计非常接近!
即使我们只使用了50%的数据集(1651张图像),我们仍然能够建模我们模型的训练行为并预测给定数量图像的模型准确度。这种方法论可以用来预测达到所需准确度所需图像的数量。当可用的数据集较小且已经证明时,这非常有用, 对深度学习模型的收敛是可能的,但需要更多的图像。图像数量预测可以用于规划和预算进一步的图像收集活动。
