使用图神经网络和LSTM进行交通预测
作者: Arash Khodadadi
创建日期: 2021/12/28
最后修改: 2023/11/22
描述: 本示例展示了如何在图上进行时间序列预测。
介绍
本示例展示了如何使用图神经网络和LSTM预测交通状况。 具体来说,我们的目标是预测给定一系列道路段交通速度历史数据的未来交通速度值。
解决此问题的一种流行方法是将每个道路段的交通速度视为一个单独的时间序列,并使用同一时间序列的过去值来预测未来值。
然而,这种方法忽略了一个道路段的交通速度与邻近段的依赖关系。为了能够考虑相邻道路的交通速度之间复杂的相互作用,我们可以将交通网络定义为一个图,并将交通速度视为该图上的信号。在本示例中,我们实现了一种能够处理图上时间序列数据的神经网络架构。 我们首先展示如何处理数据并创建一个 tf.data.Dataset用于图上的预测。然后,我们实现一个模型,该模型使用图卷积和LSTM层在图上执行预测。
数据处理和模型架构的灵感来自以下论文:
Yu, Bing, Haoteng Yin, 和 Zhanxing Zhu. "时空图卷积网络:用于交通预测的深度学习框架。" 第27届国际联合人工智能大会论文集,2018。 (github)
设置
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import pandas as pd
import numpy as np
import typing
import matplotlib.pyplot as plt
import tensorflow as tf
import keras
from keras import layers
from keras import ops
数据准备
数据描述
我们使用一个真实世界的交通速度数据集,名为 PeMSD7。我们使用的是 Yu et al., 2018 收集和准备的版本,具体可在 这里 获取。
该数据集包含两个文件:
PeMSD7_W_228.csv包含加州第7区228个站点之间的距离。PeMSD7_V_228.csv包含2012年5月和6月工作日收集的这些站点的交通速度。
数据集的完整描述可以在 Yu et al., 2018 找到。
加载数据
url = "https://github.com/VeritasYin/STGCN_IJCAI-18/raw/master/dataset/PeMSD7_Full.zip"
data_dir = keras.utils.get_file(origin=url, extract=True, archive_format="zip")
data_dir = data_dir.rstrip("PeMSD7_Full.zip")
route_distances = pd.read_csv(
os.path.join(data_dir, "PeMSD7_W_228.csv"), header=None
).to_numpy()
speeds_array = pd.read_csv(
os.path.join(data_dir, "PeMSD7_V_228.csv"), header=None
).to_numpy()
print(f"route_distances shape={route_distances.shape}")
print(f"speeds_array shape={speeds_array.shape}")
route_distances shape=(228, 228)
speeds_array shape=(12672, 228)
子采样道路
为了减少问题的规模并加快训练速度,我们将仅使用数据集中228条道路中的26条样本。我们从道路0开始,选择与其最接近的5条道路,并继续这一过程,直到我们得到25条道路。您可以选择其他任何道路子集。我们这样选择道路是为了增加有相关速度时间序列的道路的可能性。sample_routes包含所选道路的ID。
sample_routes = [
0,
1,
4,
7,
8,
11,
15,
108,
109,
114,
115,
118,
120,
123,
124,
126,
127,
129,
130,
132,
133,
136,
139,
144,
147,
216,
]
route_distances = route_distances[np.ix_(sample_routes, sample_routes)]
speeds_array = speeds_array[:, sample_routes]
print(f"route_distances shape={route_distances.shape}")
print(f"speeds_array shape={speeds_array.shape}")
route_distances shape=(26, 26)
speeds_array shape=(12672, 26)
数据可视化
以下是两条路线的交通速度时间序列:
plt.figure(figsize=(18, 6))
plt.plot(speeds_array[:, [0, -1]])
plt.legend(["route_0", "route_25"])
<matplotlib.legend.Legend at 0x7f5a870b2050>
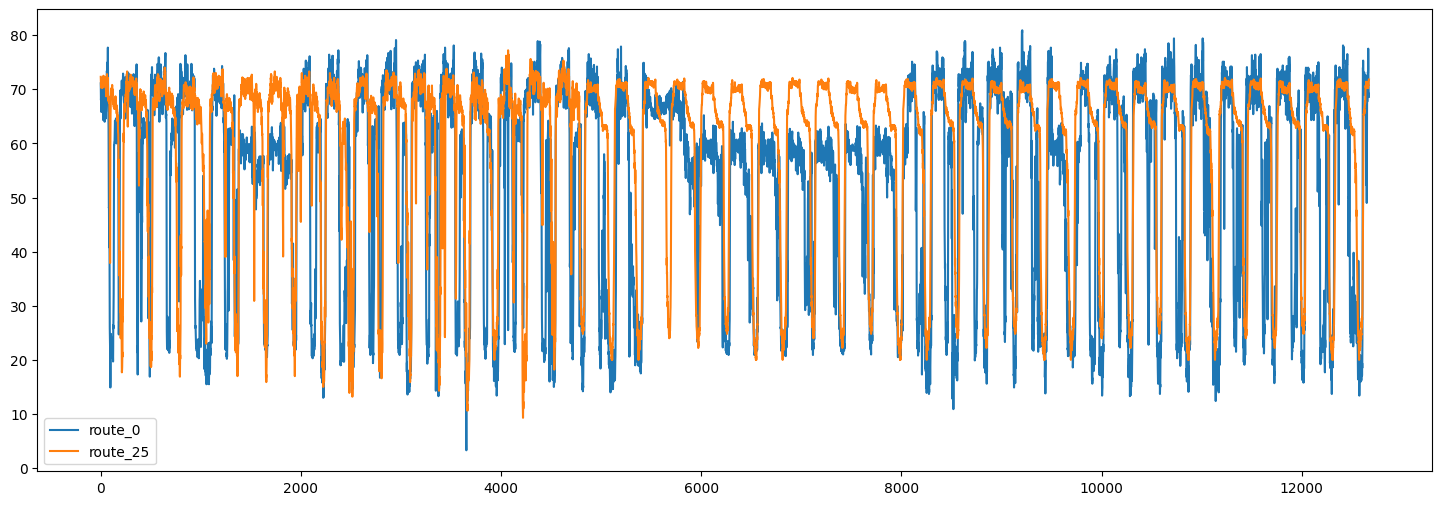
我们还可以可视化不同路线间时间序列的相关性。
plt.figure(figsize=(8, 8))
plt.matshow(np.corrcoef(speeds_array.T), 0)
plt.xlabel("道路编号")
plt.ylabel("道路编号")
Text(0, 0.5, '道路编号')
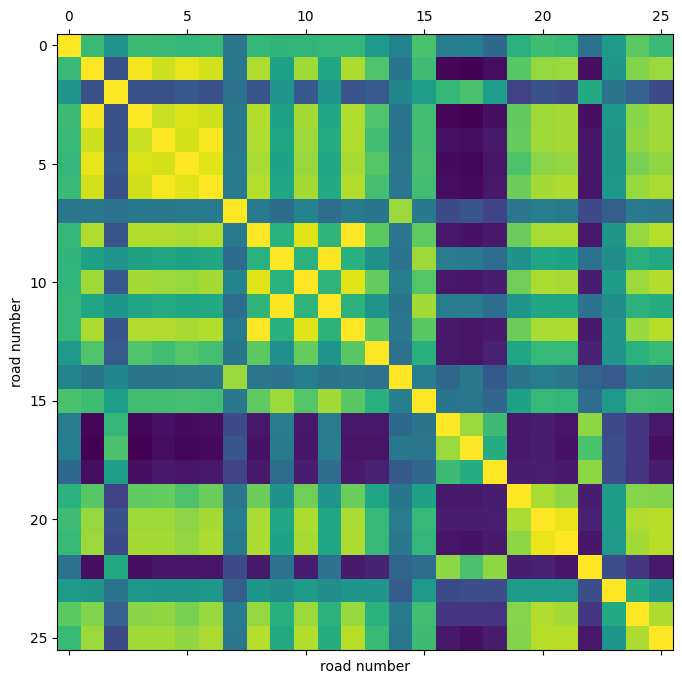
通过这个相关性热图,我们可以看到,例如4、5、6号路线的速度高度相关。
拆分和标准化数据
接下来,我们将速度值数组拆分为训练/验证/测试集,并标准化结果数组:
train_size, val_size = 0.5, 0.2
def preprocess(data_array: np.ndarray, train_size: float, val_size: float):
"""将数据拆分为训练/验证/测试集并对数据进行标准化。
参数:
data_array: 形状为 `(num_time_steps, num_routes)` 的ndarray
train_size: 介于0.0和1.0之间的浮动值,表示数据集中训练集的比例。
val_size: 介于0.0和1.0之间的浮动值,表示数据集中验证集的比例。
返回:
`train_array`, `val_array`, `test_array`
"""
num_time_steps = data_array.shape[0]
num_train, num_val = (
int(num_time_steps * train_size),
int(num_time_steps * val_size),
)
train_array = data_array[:num_train]
mean, std = train_array.mean(axis=0), train_array.std(axis=0)
train_array = (train_array - mean) / std
val_array = (data_array[num_train : (num_train + num_val)] - mean) / std
test_array = (data_array[(num_train + num_val) :] - mean) / std
return train_array, val_array, test_array
train_array, val_array, test_array = preprocess(speeds_array, train_size, val_size)
print(f"训练集大小: {train_array.shape}")
print(f"验证集大小: {val_array.shape}")
print(f"测试集大小: {test_array.shape}")
训练集大小: (6336, 26)
验证集大小: (2534, 26)
测试集大小: (3802, 26)
创建 TensorFlow 数据集
接下来,我们为我们的预测问题创建数据集。预测问题可以表述为:给定时间 t+1, t+2, ..., t+T 的道路速度值序列,我们希望预测时间 t+T+1, ..., t+T+h 的道路速度的未来值。因此,对于每个时间 t,我们模型的输入是 T 个大小为 N 的向量,目标是 h 个大小为 N 的向量,其中 N 是道路的数量。
我们使用 Keras 内置函数 keras.utils.timeseries_dataset_from_array。下面的函数 create_tf_dataset() 接受一个 numpy.ndarray 作为输入,并返回一个 tf.data.Dataset。在此函数中 input_sequence_length=T 和 forecast_horizon=h。
参数 multi_horizon 需要更多解释。假设 forecast_horizon=3。如果 multi_horizon=True,则模型将对时间步 t+T+1, t+T+2, t+T+3 进行预测。因此,目标将具有形状 (T,3)。但如果 multi_horizon=False,模型将仅对时间步 t+T+3 进行预测,因此目标将具有形状 (T, 1)。
您可能会注意到,每个批次中的输入张量的形状为 (batch_size, input_sequence_length, num_routes, 1)。最后一个维度的添加是为了使模型更通用:在每个时间步, 每条道路的输入特征可能包含多个时间序列。例如,可能希望在历史速度值的基础上,额外使用温度时间序列作为输入特征。在这个例子中,输入的最后一个维度始终为1。
我们使用每条道路最近的12个速度值来预测接下来3个时间步的速度:
batch_size = 64
input_sequence_length = 12
forecast_horizon = 3
multi_horizon = False
def create_tf_dataset(
data_array: np.ndarray,
input_sequence_length: int,
forecast_horizon: int,
batch_size: int = 128,
shuffle=True,
multi_horizon=True,
):
"""从numpy数组创建tensorflow数据集。
该函数创建一个数据集,其中每个元素是一个元组 `(inputs, targets)`。
`inputs` 是一个形状为 `(batch_size, input_sequence_length, num_routes, 1)` 的张量,包含
每个节点的时间序列的 `input_sequence_length` 个过去值。
`targets` 是一个形状为 `(batch_size, forecast_horizon, num_routes)` 的张量,
包含每个节点的时间序列的 `forecast_horizon`
个未来值。
参数:
data_array: 形状为 `(num_time_steps, num_routes)` 的 np.ndarray
input_sequence_length: 输入序列的长度(以时间步数计算)。
forecast_horizon: 如果 `multi_horizon=True`,目标将是时间序列在未来 1 到 `forecast_horizon` 个时间步的值。
如果 `multi_horizon=False`,目标将是时间序列在 `forecast_horizon` 步后的值(仅一个值)。
batch_size: 每个批次中的时间序列样本数量。
shuffle: 是否对输出样本进行洗牌,或者按时间顺序提取它们。
multi_horizon: 见 `forecast_horizon`。
返回:
tf.data.Dataset 实例。
"""
inputs = keras.utils.timeseries_dataset_from_array(
np.expand_dims(data_array[:-forecast_horizon], axis=-1),
None,
sequence_length=input_sequence_length,
shuffle=False,
batch_size=batch_size,
)
target_offset = (
input_sequence_length
if multi_horizon
else input_sequence_length + forecast_horizon - 1
)
target_seq_length = forecast_horizon if multi_horizon else 1
targets = keras.utils.timeseries_dataset_from_array(
data_array[target_offset:],
None,
sequence_length=target_seq_length,
shuffle=False,
batch_size=batch_size,
)
dataset = tf.data.Dataset.zip((inputs, targets))
if shuffle:
dataset = dataset.shuffle(100)
return dataset.prefetch(16).cache()
train_dataset, val_dataset = (
create_tf_dataset(data_array, input_sequence_length, forecast_horizon, batch_size)
for data_array in [train_array, val_array]
)
test_dataset = create_tf_dataset(
test_array,
input_sequence_length,
forecast_horizon,
batch_size=test_array.shape[0],
shuffle=False,
multi_horizon=multi_horizon,
)
道路图
如前所述,我们假设道路段形成一个图。
PeMSD7数据集包含道路段的距离。下一步是根据这些距离创建图的邻接矩阵。按照Yu et al., 2018(公式10),我们认为如果相应道路之间的距离小于某个阈值,则图中的两个节点之间存在一条边。
def compute_adjacency_matrix(
route_distances: np.ndarray, sigma2: float, epsilon: float
):
"""从距离矩阵计算邻接矩阵。
它使用 https://github.com/VeritasYin/STGCN_IJCAI-18#data-preprocessing 中的公式计算邻接矩阵。
该实现遵循该论文。
Args:
route_distances: 形状为 `(num_routes, num_routes)` 的 np.ndarray。该数组的条目 `i,j` 是
道路 `i,j` 之间的距离。
sigma2: 决定应用于平方距离矩阵的高斯核的宽度。
epsilon: 指定两个节点之间是否存在边的阈值。具体而言,`A[i,j]=1`
如果 `np.exp(-w2[i,j] / sigma2) >= epsilon`,否则 `A[i,j]=0`,其中 `A` 是邻接
矩阵,`w2=route_distances * route_distances`
Returns:
一个布尔图邻接矩阵。
"""
num_routes = route_distances.shape[0]
route_distances = route_distances / 10000.0
w2, w_mask = (
route_distances * route_distances,
np.ones([num_routes, num_routes]) - np.identity(num_routes),
)
return (np.exp(-w2 / sigma2) >= epsilon) * w_mask
函数 compute_adjacency_matrix() 返回一个布尔邻接矩阵,
其中 1 表示两个节点之间存在边。我们使用以下类来存储图的信息。
class GraphInfo:
def __init__(self, edges: typing.Tuple[list, list], num_nodes: int):
self.edges = edges
self.num_nodes = num_nodes
sigma2 = 0.1
epsilon = 0.5
adjacency_matrix = compute_adjacency_matrix(route_distances, sigma2, epsilon)
node_indices, neighbor_indices = np.where(adjacency_matrix == 1)
graph = GraphInfo(
edges=(node_indices.tolist(), neighbor_indices.tolist()),
num_nodes=adjacency_matrix.shape[0],
)
print(f"节点数量: {graph.num_nodes}, 边数量: {len(graph.edges[0])}")
节点数量: 26, 边数量: 150
网络架构
我们的模型用于在图上进行预测,由一个图卷积层和一个 LSTM 层组成。
图卷积层
我们对图卷积层的实现类似于this Keras example中的实现。请注意,在该示例中,层的输入是一个形状为(num_nodes,in_feat)的 2D 张量,但在我们的示例中,层的输入是一个形状为(num_nodes, batch_size, input_seq_length, in_feat)的 4D 张量。图卷积层执行以下步骤:
- 节点的表示在
self.compute_nodes_representation()中通过将输入特征乘以self.weight进行计算 - 聚合邻居消息在
self.compute_aggregated_messages()中进行计算,首先聚合邻居的表示,然后将结果乘以self.weight - 层的最终输出在
self.update()中通过结合节点表示和邻居的聚合消息进行计算
class GraphConv(layers.Layer):
def __init__(
self,
in_feat,
out_feat,
graph_info: GraphInfo,
aggregation_type="mean",
combination_type="concat",
activation: typing.Optional[str] = None,
**kwargs,
):
super().__init__(**kwargs)
self.in_feat = in_feat
self.out_feat = out_feat
self.graph_info = graph_info
self.aggregation_type = aggregation_type
self.combination_type = combination_type
self.weight = self.add_weight(
initializer=keras.initializers.GlorotUniform(),
shape=(in_feat, out_feat),
dtype="float32",
trainable=True,
)
self.activation = layers.Activation(activation)
def aggregate(self, neighbour_representations):
aggregation_func = {
"sum": tf.math.unsorted_segment_sum,
"mean": tf.math.unsorted_segment_mean,
"max": tf.math.unsorted_segment_max,
}.get(self.aggregation_type)
if aggregation_func:
return aggregation_func(
neighbour_representations,
self.graph_info.edges[0],
num_segments=self.graph_info.num_nodes,
)
raise ValueError(f"Invalid aggregation type: {self.aggregation_type}")
def compute_nodes_representation(self, features):
"""计算每个节点的表示。
节点的表示是通过将特征张量与
`self.weight` 相乘获得的。注意,
`self.weight` 的形状为 `(in_feat, out_feat)`。
Args:
features: 形状为 `(num_nodes, batch_size, input_seq_len, in_feat)` 的张量
Returns:
形状为 `(num_nodes, batch_size, input_seq_len, out_feat)` 的张量
"""
return ops.matmul(features, self.weight)
def compute_aggregated_messages(self, features):
neighbour_representations = tf.gather(features, self.graph_info.edges[1])
aggregated_messages = self.aggregate(neighbour_representations)
return ops.matmul(aggregated_messages, self.weight)
def update(self, nodes_representation, aggregated_messages):
if self.combination_type == "concat":
h = ops.concatenate([nodes_representation, aggregated_messages], axis=-1)
elif self.combination_type == "add":
h = nodes_representation + aggregated_messages
else:
raise ValueError(f"Invalid combination type: {self.combination_type}.")
return self.activation(h)
def call(self, features):
"""前向传播。
Args:
features: 形状为 `(num_nodes, batch_size, input_seq_len, in_feat)` 的张量
Returns:
形状为 `(num_nodes, batch_size, input_seq_len, out_feat)` 的张量
"""
nodes_representation = self.compute_nodes_representation(features)
aggregated_messages = self.compute_aggregated_messages(features)
return self.update(nodes_representation, aggregated_messages)
LSTM加图卷积
通过将图卷积层应用于输入张量,我们得到了另一个张量,包含了节点在时间上的表示(另一个4D张量)。对于每个时间步,节点的表示受到其邻居信息的影响。
然而,要做出良好的预测,我们不仅需要来自邻居的信息,还需要对信息进行时间处理。为此,我们可以将每个节点的张量通过一个递归层。下面的LSTMGC层首先对输入应用图卷积层,然后将结果传递通过一个LSTM层。
class LSTMGC(layers.Layer):
"""由卷积层、LSTM层和稠密层组成的层。"""
def __init__(
self,
in_feat,
out_feat,
lstm_units: int,
input_seq_len: int,
output_seq_len: int,
graph_info: GraphInfo,
graph_conv_params: typing.Optional[dict] = None,
**kwargs,
):
super().__init__(**kwargs)
# 图卷积层
if graph_conv_params is None:
graph_conv_params = {
"aggregation_type": "mean",
"combination_type": "concat",
"activation": None,
}
self.graph_conv = GraphConv(in_feat, out_feat, graph_info, **graph_conv_params)
self.lstm = layers.LSTM(lstm_units, activation="relu")
self.dense = layers.Dense(output_seq_len)
self.input_seq_len, self.output_seq_len = input_seq_len, output_seq_len
def call(self, inputs):
"""前向传播。
Args:
inputs: 形状为`(batch_size, input_seq_len, num_nodes, in_feat)`的张量
Returns:
形状为`(batch_size, output_seq_len, num_nodes)`的张量。
"""
# 转换形状为( num_nodes, batch_size, input_seq_len, in_feat )
inputs = ops.transpose(inputs, [2, 0, 1, 3])
gcn_out = self.graph_conv(
inputs
) # gcn_out的形状为: (num_nodes, batch_size, input_seq_len, out_feat)
shape = ops.shape(gcn_out)
num_nodes, batch_size, input_seq_len, out_feat = (
shape[0],
shape[1],
shape[2],
shape[3],
)
# LSTM只接受3D张量作为输入
gcn_out = ops.reshape(
gcn_out, (batch_size * num_nodes, input_seq_len, out_feat)
)
lstm_out = self.lstm(
gcn_out
) # lstm_out的形状为: (batch_size * num_nodes, lstm_units)
dense_output = self.dense(
lstm_out
) # dense_output的形状为: (batch_size * num_nodes, output_seq_len)
output = ops.reshape(dense_output, (num_nodes, batch_size, self.output_seq_len))
return ops.transpose(
output, [1, 2, 0]
) # 返回形状为(batch_size, output_seq_len, num_nodes)的张量
模型训练
in_feat = 1
batch_size = 64
epochs = 20
input_sequence_length = 12
forecast_horizon = 3
multi_horizon = False
out_feat = 10
lstm_units = 64
graph_conv_params = {
"aggregation_type": "mean",
"combination_type": "concat",
"activation": None,
}
st_gcn = LSTMGC(
in_feat,
out_feat,
lstm_units,
input_sequence_length,
forecast_horizon,
graph,
graph_conv_params,
)
inputs = layers.Input((input_sequence_length, graph.num_nodes, in_feat))
outputs = st_gcn(inputs)
model = keras.models.Model(inputs, outputs)
model.compile(
optimizer=keras.optimizers.RMSprop(learning_rate=0.0002),
loss=keras.losses.MeanSquaredError(),
)
model.fit(
train_dataset,
validation_data=val_dataset,
epochs=epochs,
callbacks=[keras.callbacks.EarlyStopping(patience=10)],
)
Epoch 1/20
1/99 [37m━━━━━━━━━━━━━━━━━━━━ 5:16 3s/step - loss: 1.0735
警告:在调用 absl::InitializeLog() 之前的所有日志消息都写入 STDERR
I0000 00:00:1700705896.341813 3354152 device_compiler.h:186] 使用 XLA 编译了集群!该行在进程生命周期内最多记录一次。
W0000 00:00:1700705896.362213 3354152 graph_launch.cc:671] 由于 memset 节点破坏了图更新,回退到逐操作模式
W0000 00:00:1700705896.363019 3354152 graph_launch.cc:671] 由于 memset 节点破坏了图更新,回退到逐操作模式
44/99 ━━━━━━━━━━━━━━━━━━━━ 1s 32ms/step - loss: 0.7919
W0000 00:00:1700705897.577991 3354154 graph_launch.cc:671] 由于 memset 节点破坏了图更新,回退到逐操作模式
W0000 00:00:1700705897.578802 3354154 graph_launch.cc:671] 由于 memset 节点破坏了图更新,回退到逐操作模式
99/99 ━━━━━━━━━━━━━━━━━━━━ 7s 36ms/step - loss: 0.7470 - val_loss: 0.3568
第 2 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.2785 - val_loss: 0.1845
第 3 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.1734 - val_loss: 0.1250
第 4 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.1313 - val_loss: 0.1084
第 5 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.1095 - val_loss: 0.0994
第 6 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0960 - val_loss: 0.0930
第 7 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0896 - val_loss: 0.0954
第 8 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0862 - val_loss: 0.0920
第 9 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - loss: 0.0841 - val_loss: 0.0898
第 10 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - loss: 0.0827 - val_loss: 0.0884
第 11 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - loss: 0.0817 - val_loss: 0.0865
第 12 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0809 - val_loss: 0.0843
第 13 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0803 - val_loss: 0.0828
第 14 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0798 - val_loss: 0.0814
第 15 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0794 - val_loss: 0.0802
第 16 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0790 - val_loss: 0.0794
第 17 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0787 - val_loss: 0.0786
第 18 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0785 - val_loss: 0.0780
第 19 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0782 - val_loss: 0.0776
第 20 轮/20
99/99 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0780 - val_loss: 0.0776
<keras.src.callbacks.history.History at 0x7f59b8152560>
在测试集上进行预测
现在我们可以使用训练好的模型对测试集进行预测。下面,我们计算模型的MAE并将其与简单预测的MAE进行比较。简单预测是每个节点的速度最后一个值。
x_test, y = next(test_dataset.as_numpy_iterator())
y_pred = model.predict(x_test)
plt.figure(figsize=(18, 6))
plt.plot(y[:, 0, 0])
plt.plot(y_pred[:, 0, 0])
plt.legend(["实际", "预测"])
naive_mse, model_mse = (
np.square(x_test[:, -1, :, 0] - y[:, 0, :]).mean(),
np.square(y_pred[:, 0, :] - y[:, 0, :]).mean(),
)
print(f"简单 MAE: {naive_mse}, 模型 MAE: {model_mse}")
119/119 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step
简单 MAE: 0.13472308593195767, 模型 MAE: 0.13524348477186485
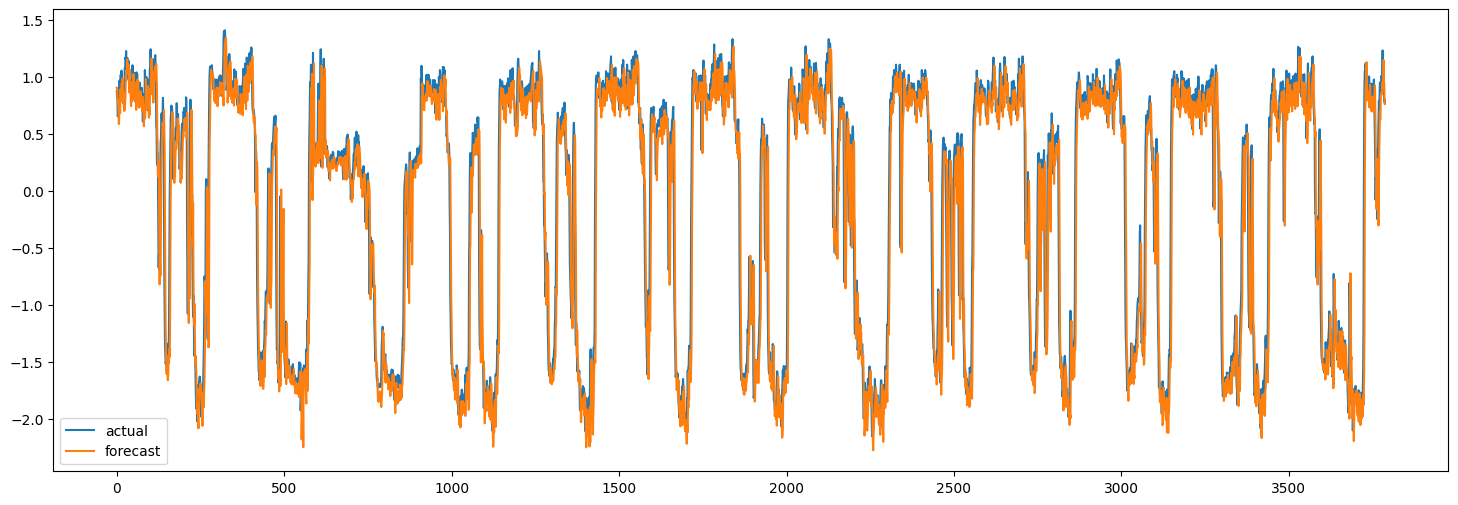
当然,这里目的是演示该方法,而不是实现最佳性能。为了提高模型的准确性,所有模型超参数都应仔细调整。此外,可以堆叠多个LSTMGC块以增加模型的表示能力。
