时间序列预测天气预测
作者: Prabhanshu Attri,Yashika Sharma,Kristi Takach,Falak Shah
创建日期: 2020/06/23
最后修改: 2023/11/22
描述: 本笔记展示如何使用 LSTM 模型进行时间序列预测。
设置
import pandas as pd
import matplotlib.pyplot as plt
import keras
气候数据时间序列
我们将使用由马克斯·普朗克生物地球化学研究所记录的耶拿气候数据集。该数据集包含 14 个特征,如温度、压力、湿度等,每 10 分钟记录一次。
位置:德国耶拿,马克斯·普朗克生物地球化学研究所的气象站
考虑的时间范围:2009年1月10日 - 2016年12月31日
下表显示了列名、它们的值格式和描述。
| 索引 | 特征 | 格式 | 描述 |
|---|---|---|---|
| 1 | 日期时间 | 01.01.2009 00:10:00 | 日期时间参考 |
| 2 | p (mbar) | 996.52 | 用于量化内部压力的帕斯卡 SI 导出单位。气象报告通常以毫巴表示大气压力。 |
| 3 | T (摄氏度) | -8.02 | 摄氏温度 |
| 4 | Tpot (开尔文) | 265.4 | 开尔文温度 |
| 5 | Tdew (摄氏度) | -8.9 | 相对于湿度的摄氏温度。露点是衡量空气中绝对水分量的指标,DP 是空气无法保持所有水分的温度,水分开始凝结。 |
| 6 | rh (%) | 93.3 | 相对湿度是衡量空气中水蒸气饱和程度的指标,%RH 决定收集对象中包含的水量。 |
| 7 | VPmax (mbar) | 3.33 | 饱和蒸汽压力 |
| 8 | VPact (mbar) | 3.11 | 蒸汽压力 |
| 9 | VPdef (mbar) | 0.22 | 蒸汽压力缺口 |
| 10 | sh (g/kg) | 1.94 | 比湿 |
| 11 | H2OC (mmol/mol) | 3.12 | 水蒸气浓度 |
| 12 | rho (g/m ** 3) | 1307.75 | 气密性 |
| 13 | wv (m/s) | 1.03 | 风速 |
| 14 | max. wv (m/s) | 1.75 | 最大风速 |
| 15 | wd (度) | 152.3 | 风向(度) |
from zipfile import ZipFile
uri = "https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip"
zip_path = keras.utils.get_file(origin=uri, fname="jena_climate_2009_2016.csv.zip")
zip_file = ZipFile(zip_path)
zip_file.extractall()
csv_path = "jena_climate_2009_2016.csv"
df = pd.read_csv(csv_path)
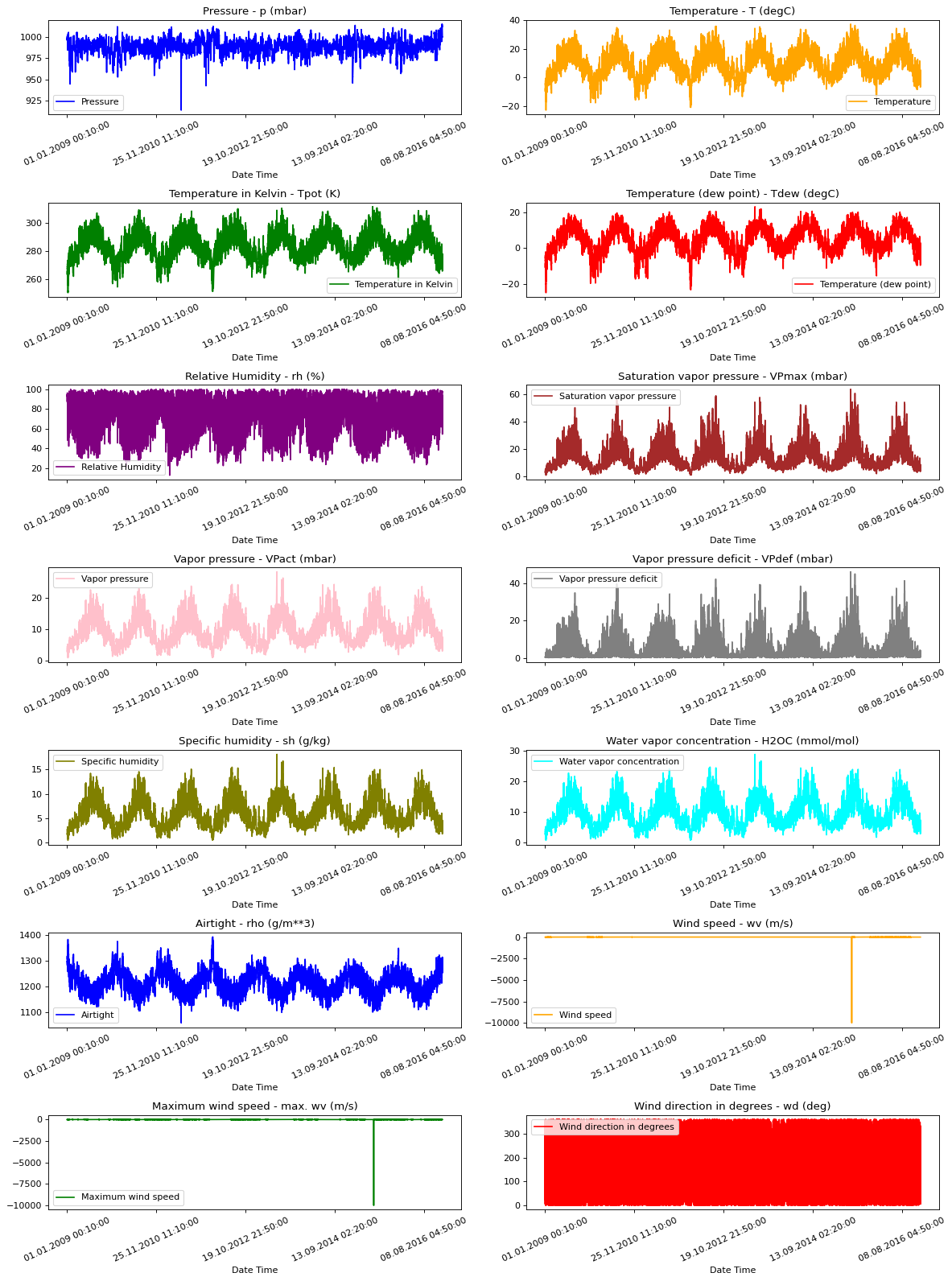
原始数据可视化
为了让我们对正在处理的数据有一个大致的了解,下面绘制了每个特征的图。这显示了 2009 年到 2016 年期间每个特征的明显模式。它还显示了数据中存在的异常情况,这些异常将在归一化过程中解决。
titles = [
"压力",
"温度",
"开尔文温度",
"露点温度",
"相对湿度",
"饱和蒸气压",
"蒸气压",
"蒸气压缺口",
"比湿",
"水蒸气浓度",
"气密性",
"风速",
"最大风速",
"风向(度)",
]
feature_keys = [
"p (mbar)",
"T (degC)",
"Tpot (K)",
"Tdew (degC)",
"rh (%)",
"VPmax (mbar)",
"VPact (mbar)",
"VPdef (mbar)",
"sh (g/kg)",
"H2OC (mmol/mol)",
"rho (g/m**3)",
"wv (m/s)",
"max. wv (m/s)",
"wd (deg)",
]
colors = [
"blue",
"orange",
"green",
"red",
"purple",
"brown",
"pink",
"gray",
"olive",
"cyan",
]
date_time_key = "日期时间"
def show_raw_visualization(data):
time_data = data[date_time_key]
fig, axes = plt.subplots(
nrows=7, ncols=2, figsize=(15, 20), dpi=80, facecolor="w", edgecolor="k"
)
for i in range(len(feature_keys)):
key = feature_keys[i]
c = colors[i % (len(colors))]
t_data = data[key]
t_data.index = time_data
t_data.head()
ax = t_data.plot(
ax=axes[i // 2, i % 2],
color=c,
title="{} - {}".format(titles[i], key),
rot=25,
)
ax.legend([titles[i]])
plt.tight_layout()
show_raw_visualization(df)
数据预处理
在这里我们选择了大约300,000个数据点进行训练。观察每10分钟记录一次,这意味着每小时6次。由于在60分钟内不会有剧烈变化,我们将重新采样每小时一个数据点。我们通过timeseries_dataset_from_array工具中的sampling_rate参数来实现。
我们正在跟踪过去720个时间戳的数据(720/6=120小时)。这些数据将用于预测72个时间戳后的温度(72/6=12小时)。
由于每个特征的值范围不同,我们在训练神经网络之前进行归一化,将特征值限制在[0, 1]的范围内。我们通过减去每个特征的均值并除以标准差来实现这一点。
71.5%的数据将用于训练模型,即300,693行。可以更改split_fraction以更改此百分比。
模型显示前5天的数据,即720个观测,每小时采样。72(12小时*每小时6次观测)次观测后的温度将用作标签。
split_fraction = 0.715
train_split = int(split_fraction * int(df.shape[0]))
step = 6
past = 720
future = 72
learning_rate = 0.001
batch_size = 256
epochs = 10
def normalize(data, train_split):
data_mean = data[:train_split].mean(axis=0)
data_std = data[:train_split].std(axis=0)
return (data - data_mean) / data_std
从相关性热图中可以看出,某些参数如相对湿度和特定湿度是冗余的。因此,我们将使用选择的特征,而不是全部。
print(
"选择的参数为:",
", ".join([titles[i] for i in [0, 1, 5, 7, 8, 10, 11]]),
)
selected_features = [feature_keys[i] for i in [0, 1, 5, 7, 8, 10, 11]]
features = df[selected_features]
features.index = df[date_time_key]
features.head()
features = normalize(features.values, train_split)
features = pd.DataFrame(features)
features.head()
train_data = features.loc[0 : train_split - 1]
val_data = features.loc[train_split:]
选择的参数为: 压力, 温度, 饱和蒸汽压, 蒸汽压缺口, 特定湿度, 气密性, 风速
训练数据集
训练数据集标签从第792个观测开始(720 + 72)。
start = past + future
end = start + train_split
x_train = train_data[[i for i in range(7)]].values
y_train = features.iloc[start:end][[1]]
sequence_length = int(past / step)
timeseries_dataset_from_array函数接收按等间隔收集的数据点序列,以及时间序列参数,如序列/窗口长度、两个序列/窗口之间的间距等,以生成从主时间序列抽样的子时间序列输入和目标的批次。
dataset_train = keras.preprocessing.timeseries_dataset_from_array(
x_train,
y_train,
sequence_length=sequence_length,
sampling_rate=step,
batch_size=batch_size,
)
验证数据集
验证数据集不能包含最后792行,因为我们不会有这些记录的标签数据,因此必须从数据末尾减去792。
验证标签数据集必须从train_split后的792开始,因此我们必须在label_start中加上past + future(792)。
x_end = len(val_data) - past - future
label_start = train_split + past + future
x_val = val_data.iloc[:x_end][[i for i in range(7)]].values
y_val = features.iloc[label_start:][[1]]
dataset_val = keras.preprocessing.timeseries_dataset_from_array(
x_val,
y_val,
sequence_length=sequence_length,
sampling_rate=step,
batch_size=batch_size,
)
for batch in dataset_train.take(1):
inputs, targets = batch
print("输入形状:", inputs.numpy().shape)
print("目标形状:", targets.numpy().shape)
输入形状: (256, 120, 7)
目标形状: (256, 1)
训练
inputs = keras.layers.Input(shape=(inputs.shape[1], inputs.shape[2]))
lstm_out = keras.layers.LSTM(32)(inputs)
outputs = keras.layers.Dense(1)(lstm_out)
model = keras.Model(inputs=inputs, outputs=outputs)
model.compile(optimizer=keras.optimizers.Adam(learning_rate=learning_rate), loss="mse")
model.summary()
CUDA后端初始化失败: 找到cuSOLVER版本11405,但JAX是基于版本11502构建的,后者较新。安装的cuSOLVER副本必须至少与JAX构建时的版本一样新。(设置TF_CPP_MIN_LOG_LEVEL=0并重新运行以获取更多信息。)
模型: "functional_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓ ┃ 层 (类型) ┃ 输出形状 ┃ 参数数量 ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩ │ input_layer (输入层) │ (None, 120, 7) │ 0 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ lstm (长短期记忆) │ (None, 32) │ 5,120 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ dense (全连接层) │ (None, 1) │ 33 │ └─────────────────────────────────┴───────────────────────────┴────────────┘
总参数: 5,153 (20.13 KB)
可训练参数: 5,153 (20.13 KB)
不可训练参数: 0 (0.00 B)
我们将使用 ModelCheckpoint 回调定期保存检查点,并使用 EarlyStopping 回调在验证损失不再改善时中断训练。
path_checkpoint = "model_checkpoint.weights.h5"
es_callback = keras.callbacks.EarlyStopping(monitor="val_loss", min_delta=0, patience=5)
modelckpt_callback = keras.callbacks.ModelCheckpoint(
monitor="val_loss",
filepath=path_checkpoint,
verbose=1,
save_weights_only=True,
save_best_only=True,
)
history = model.fit(
dataset_train,
epochs=epochs,
validation_data=dataset_val,
callbacks=[es_callback, modelckpt_callback],
)
Epoch 1/10
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 70ms/step - loss: 0.3008
Epoch 1: val_loss 从 inf 改进到 0.15039,保存模型到 model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 104s 88ms/step - loss: 0.3007 - val_loss: 0.1504
Epoch 2/10
1171/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 66ms/step - loss: 0.1397
Epoch 2: val_loss 从 0.15039 改进到 0.14231,保存模型到 model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 97s 83ms/step - loss: 0.1396 - val_loss: 0.1423
Epoch 3/10
1171/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 69ms/step - loss: 0.1242
Epoch 3: val_loss 没有从 0.14231 改进
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 101s 86ms/step - loss: 0.1242 - val_loss: 0.1513
Epoch 4/10
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 68ms/step - loss: 0.1182
Epoch 4: val_loss 没有从 0.14231 改进
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 102s 87ms/step - loss: 0.1182 - val_loss: 0.1503
Epoch 5/10
1171/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 67ms/step - loss: 0.1160
Epoch 5: val_loss 没有从 0.14231 改进
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 100s 85ms/step - loss: 0.1160 - val_loss: 0.1500
Epoch 6/10
1171/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 69ms/step - loss: 0.1130
Epoch 6: val_loss 没有从 0.14231 改进
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 100s 86ms/step - loss: 0.1130 - val_loss: 0.1469
Epoch 7/10
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 70ms/step - loss: 0.1106
Epoch 7: val_loss 从 0.14231 改进到 0.13916,保存模型到 model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 104s 89ms/step - loss: 0.1106 - val_loss: 0.1392
Epoch 8/10
1171/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 66ms/step - loss: 0.1097
Epoch 8: val_loss 从 0.13916 改进到 0.13257,保存模型到 model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 98s 84ms/step - loss: 0.1097 - val_loss: 0.1326
Epoch 9/10
1171/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 68ms/step - loss: 0.1075
Epoch 9: val_loss 从 0.13257 改进到 0.13057,保存模型到 model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 100s 85ms/step - loss: 0.1075 - val_loss: 0.1306
Epoch 10/10
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 66ms/step - loss: 0.1065
Epoch 10: val_loss 从 0.13057 改进到 0.12671,保存模型到 model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 98s 84ms/step - loss: 0.1065 - val_loss: 0.1267
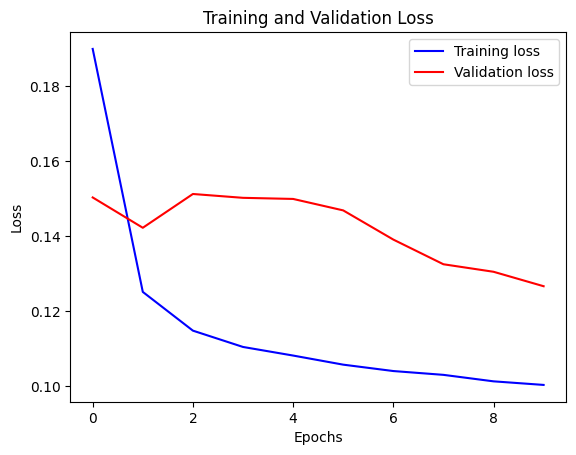
我们可以用下面的函数可视化损失。在某一点后,损失停止下降。
def visualize_loss(history, title):
loss = history.history["loss"]
val_loss = history.history["val_loss"]
epochs = range(len(loss))
plt.figure()
plt.plot(epochs, loss, "b", label="训练损失")
plt.plot(epochs, val_loss, "r", label="验证损失")
plt.title(title)
plt.xlabel("轮次")
plt.ylabel("损失")
plt.legend()
plt.show()
visualize_loss(history, "训练和验证损失")
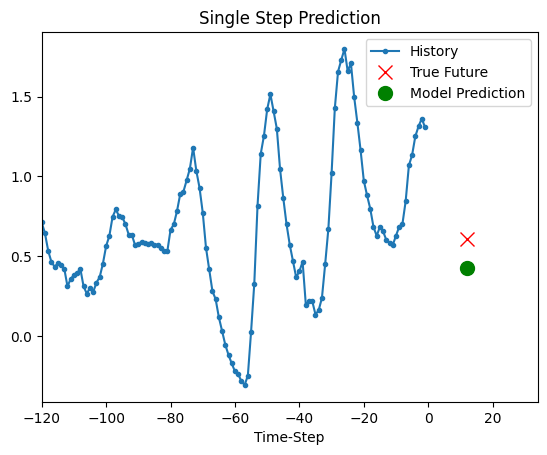
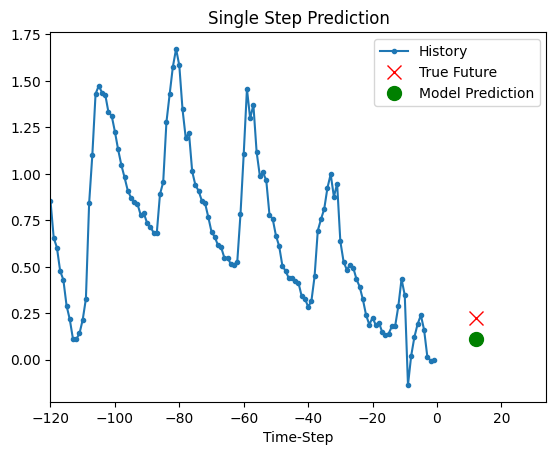
预测
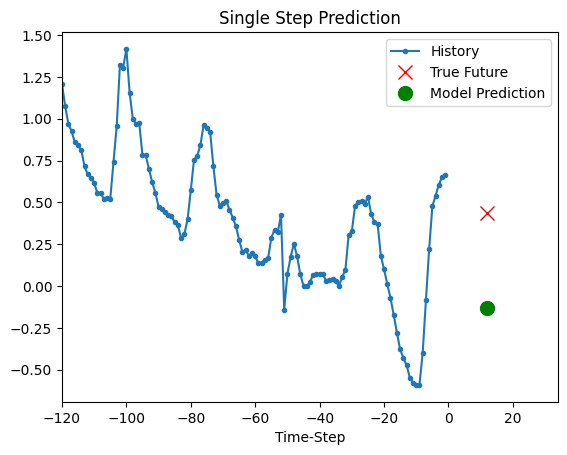
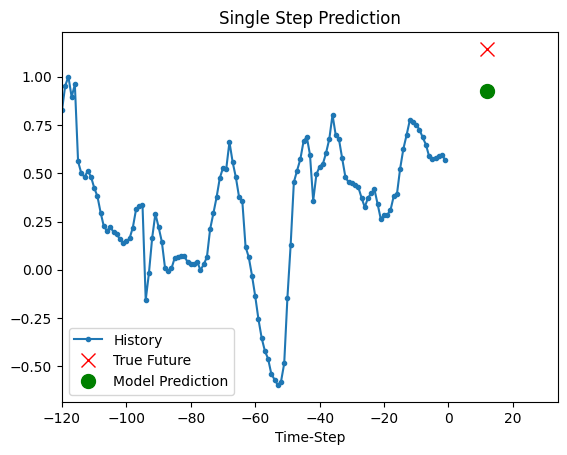
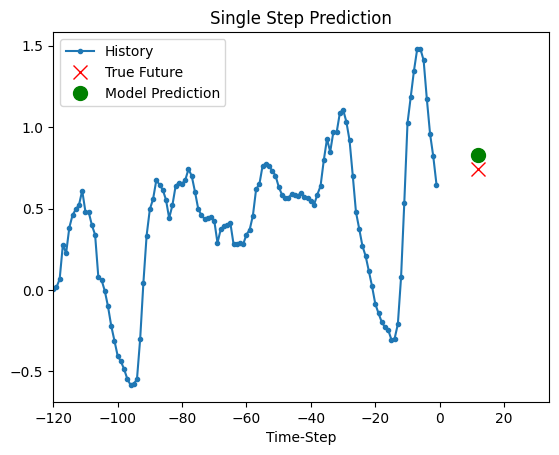
上面的训练模型现在能够对验证集中的5组值进行预测。
def show_plot(plot_data, delta, title):
labels = ["历史", "真实未来", "模型预测"]
marker = [".-", "rx", "go"]
time_steps = list(range(-(plot_data[0].shape[0]), 0))
if delta:
future = delta
else:
future = 0
plt.title(title)
for i, val in enumerate(plot_data):
if i:
plt.plot(future, plot_data[i], marker[i], markersize=10, label=labels[i])
else:
plt.plot(time_steps, plot_data[i].flatten(), marker[i], label=labels[i])
plt.legend()
plt.xlim([time_steps[0], (future + 5) * 2])
plt.xlabel("时间步")
plt.show()
return
for x, y in dataset_val.take(5):
show_plot(
[x[0][:, 1].numpy(), y[0].numpy(), model.predict(x)[0]],
12,
"单步预测",
)
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step