紧凑卷积变换器
作者: Sayak Paul
创建日期: 2021/06/30
最后修改日期: 2023/08/07
描述: 用于高效图像分类的紧凑卷积变换器。
正如在视觉变换器(ViT)论文中所讨论的,基于变换器的视觉架构通常需要比通常情况更大的数据集,以及更长的预训练时间。ImageNet-1k(大约有一百万张图像)被认为是在 ViTs 相关的中型数据范围内。这主要是因为,与 CNN 不同,ViTs(或典型的基于变换器的架构)没有良好的归纳偏见(例如,用于处理图像的卷积)。这就引出了一个问题:我们能否将卷积的优势与变换器的优势结合在一个网络架构中?这些优势包括参数效率,以及自注意力用于处理长程和全局依赖(图像中不同区域之间的相互作用)。
在用紧凑变换器逃离大数据范式中,Hassani等人提出了一种准确做到这一点的方法。他们提出了紧凑卷积变换器(CCT)架构。在这个示例中,我们将实现 CCT,并观察它在 CIFAR-10 数据集上的表现。
如果您对自注意力或变换器的概念不熟悉,可以阅读 François Chollet 的书 Deep Learning with Python 中的this chapter。此示例使用了另一个示例中的代码片段,使用视觉变换器进行图像分类。
导入
from keras import layers
import keras
import matplotlib.pyplot as plt
import numpy as np
超参数和常量
positional_emb = True
conv_layers = 2
projection_dim = 128
num_heads = 2
transformer_units = [
projection_dim,
projection_dim,
]
transformer_layers = 2
stochastic_depth_rate = 0.1
learning_rate = 0.001
weight_decay = 0.0001
batch_size = 128
num_epochs = 30
image_size = 32
加载 CIFAR-10 数据集
num_classes = 10
input_shape = (32, 32, 3)
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print(f"x_train shape: {x_train.shape} - y_train shape: {y_train.shape}")
print(f"x_test shape: {x_test.shape} - y_test shape: {y_test.shape}")
x_train shape: (50000, 32, 32, 3) - y_train shape: (50000, 10)
x_test shape: (10000, 32, 32, 3) - y_test shape: (10000, 10)
CCT 标记器
CCT 作者介绍的第一个方案是用于处理图像的标记器。在标准的 ViT 中,图像被组织成均匀的非重叠补丁。这消除了不同补丁之间存在的边界级信息。这对于神经网络有效利用局部信息至关重要。下图展示了图像是如何组织成补丁的。

我们已经知道卷积在利用局部信息方面非常优秀。因此,基于这一点,作者引入了一种全卷积小型网络来生成图像补丁。
class CCTTokenizer(layers.Layer):
def __init__(
self,
kernel_size=3,
stride=1,
padding=1,
pooling_kernel_size=3,
pooling_stride=2,
num_conv_layers=conv_layers,
num_output_channels=[64, 128],
positional_emb=positional_emb,
**kwargs,
):
super().__init__(**kwargs)
# 这是我们的分词器。
self.conv_model = keras.Sequential()
for i in range(num_conv_layers):
self.conv_model.add(
layers.Conv2D(
num_output_channels[i],
kernel_size,
stride,
padding="valid",
use_bias=False,
activation="relu",
kernel_initializer="he_normal",
)
)
self.conv_model.add(layers.ZeroPadding2D(padding))
self.conv_model.add(
layers.MaxPooling2D(pooling_kernel_size, pooling_stride, "same")
)
self.positional_emb = positional_emb
def call(self, images):
outputs = self.conv_model(images)
# 在通过我们的迷你网络传递图像后,空间维度会被展平以形成序列。
reshaped = keras.ops.reshape(
outputs,
(
-1,
keras.ops.shape(outputs)[1] * keras.ops.shape(outputs)[2],
keras.ops.shape(outputs)[-1],
),
)
return reshaped
Positional embeddings 在 CCT 中是可选的。如果我们想使用它们,可以使用下面定义的层。
class PositionEmbedding(keras.layers.Layer):
def __init__(
self,
sequence_length,
initializer="glorot_uniform",
**kwargs,
):
super().__init__(**kwargs)
if sequence_length is None:
raise ValueError("`sequence_length` 必须是一个整数,接收到 `None`。")
self.sequence_length = int(sequence_length)
self.initializer = keras.initializers.get(initializer)
def get_config(self):
config = super().get_config()
config.update(
{
"sequence_length": self.sequence_length,
"initializer": keras.initializers.serialize(self.initializer),
}
)
return config
def build(self, input_shape):
feature_size = input_shape[-1]
self.position_embeddings = self.add_weight(
name="embeddings",
shape=[self.sequence_length, feature_size],
initializer=self.initializer,
trainable=True,
)
super().build(input_shape)
def call(self, inputs, start_index=0):
shape = keras.ops.shape(inputs)
feature_length = shape[-1]
sequence_length = shape[-2]
# 修剪以匹配输入序列的长度,可能会小于层的 sequence_length。
position_embeddings = keras.ops.convert_to_tensor(self.position_embeddings)
position_embeddings = keras.ops.slice(
position_embeddings,
(start_index, 0),
(sequence_length, feature_length),
)
return keras.ops.broadcast_to(position_embeddings, shape)
def compute_output_shape(self, input_shape):
return input_shape
序列池化
在 CCT 中引入的另一个方法是注意力池化或序列池化。在 ViT 中,只有与类标记对应的特征图被池化,然后用于后续的分类任务(或任何其他下游任务)。
class SequencePooling(layers.Layer):
def __init__(self):
super().__init__()
self.attention = layers.Dense(1)
def call(self, x):
attention_weights = keras.ops.softmax(self.attention(x), axis=1)
attention_weights = keras.ops.transpose(attention_weights, axes=(0, 2, 1))
weighted_representation = keras.ops.matmul(attention_weights, x)
return keras.ops.squeeze(weighted_representation, -2)
随机深度正则化
随机深度是一种正则化技术,随机丢弃一组层。在推理过程中,层保持原样。这与 Dropout 非常相似,但它是在一组层上操作,而不是在单个节点上。在 CCT 中,随机深度在 Transformers 编码器的残差模块之前使用。
# 来源于: github.com:rwightman/pytorch-image-models.
class StochasticDepth(layers.Layer):
def __init__(self, drop_prop, **kwargs):
super().__init__(**kwargs)
self.drop_prob = drop_prop
self.seed_generator = keras.random.SeedGenerator(1337)
def call(self, x, training=None):
if training:
keep_prob = 1 - self.drop_prob
shape = (keras.ops.shape(x)[0],) + (1,) * (len(x.shape) - 1)
random_tensor = keep_prob + keras.random.uniform(
shape, 0, 1, seed=self.seed_generator
)
random_tensor = keras.ops.floor(random_tensor)
return (x / keep_prob) * random_tensor
return x
变换器编码器的 MLP
def mlp(x, hidden_units, dropout_rate):
for units in hidden_units:
x = layers.Dense(units, activation=keras.ops.gelu)(x)
x = layers.Dropout(dropout_rate)(x)
return x
数据增强
在原始论文中,作者使用AutoAugment引入更强的正则化。对于这个例子,我们将使用标准的几何增强,比如随机裁剪和翻转。
# 注意重新缩放层。这些层具有预定义的推理行为。
data_augmentation = keras.Sequential(
[
layers.Rescaling(scale=1.0 / 255),
layers.RandomCrop(image_size, image_size),
layers.RandomFlip("horizontal"),
],
name="data_augmentation",
)
最终的 CCT 模型
在 CCT 中,变换器编码器的输出被加权然后传递给最终的任务特定层(在本例中,我们进行分类)。
def create_cct_model(
image_size=image_size,
input_shape=input_shape,
num_heads=num_heads,
projection_dim=projection_dim,
transformer_units=transformer_units,
):
inputs = layers.Input(input_shape)
# 数据增强。
augmented = data_augmentation(inputs)
# 编码补丁。
cct_tokenizer = CCTTokenizer()
encoded_patches = cct_tokenizer(augmented)
# 应用位置嵌入。
if positional_emb:
sequence_length = encoded_patches.shape[1]
encoded_patches += PositionEmbedding(sequence_length=sequence_length)(
encoded_patches
)
# 计算随机深度概率。
dpr = [x for x in np.linspace(0, stochastic_depth_rate, transformer_layers)]
# 创建多个变换器块层。
for i in range(transformer_layers):
# 层归一化 1。
x1 = layers.LayerNormalization(epsilon=1e-5)(encoded_patches)
# 创建一个多头注意力层。
attention_output = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=projection_dim, dropout=0.1
)(x1, x1)
# 跳跃连接 1。
attention_output = StochasticDepth(dpr[i])(attention_output)
x2 = layers.Add()([attention_output, encoded_patches])
# 层归一化 2。
x3 = layers.LayerNormalization(epsilon=1e-5)(x2)
# MLP。
x3 = mlp(x3, hidden_units=transformer_units, dropout_rate=0.1)
# 跳跃连接 2。
x3 = StochasticDepth(dpr[i])(x3)
encoded_patches = layers.Add()([x3, x2])
# 应用序列池化。
representation = layers.LayerNormalization(epsilon=1e-5)(encoded_patches)
weighted_representation = SequencePooling()(representation)
# 分类输出。
logits = layers.Dense(num_classes)(weighted_representation)
# 创建 Keras 模型。
model = keras.Model(inputs=inputs, outputs=logits)
return model
模型训练和评估
def run_experiment(model):
optimizer = keras.optimizers.AdamW(learning_rate=0.001, weight_decay=0.0001)
model.compile(
optimizer=optimizer,
loss=keras.losses.CategoricalCrossentropy(
from_logits=True, label_smoothing=0.1
),
metrics=[
keras.metrics.CategoricalAccuracy(name="accuracy"),
keras.metrics.TopKCategoricalAccuracy(5, name="top-5-accuracy"),
],
)
checkpoint_filepath = "/tmp/checkpoint.weights.h5"
checkpoint_callback = keras.callbacks.ModelCheckpoint(
checkpoint_filepath,
monitor="val_accuracy",
save_best_only=True,
save_weights_only=True,
)
history = model.fit(
x=x_train,
y=y_train,
batch_size=batch_size,
epochs=num_epochs,
validation_split=0.1,
callbacks=[checkpoint_callback],
)
model.load_weights(checkpoint_filepath)
_, accuracy, top_5_accuracy = model.evaluate(x_test, y_test)
print(f"测试准确率: {round(accuracy * 100, 2)}%")
print(f"测试前 5 准确率: {round(top_5_accuracy * 100, 2)}%")
return history
cct_model = create_cct_model()
history = run_experiment(cct_model)
第 1 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 90s 248ms/步 - 准确率: 0.2578 - 损失: 2.0882 - 前 5 名准确率: 0.7553 - 验证准确率: 0.4438 - 验证损失: 1.6872 - 验证前 5 名准确率: 0.9046
第 2 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 91s 258ms/步 - 准确率: 0.4779 - 损失: 1.6074 - 前 5 名准确率: 0.9261 - 验证准确率: 0.5730 - 验证损失: 1.4462 - 验证前 5 名准确率: 0.9562
第 3 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 260ms/步 - 准确率: 0.5655 - 损失: 1.4371 - 前 5 名准确率: 0.9501 - 验证准确率: 0.6178 - 验证损失: 1.3458 - 验证前 5 名准确率: 0.9626
第 4 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 261ms/步 - 准确率: 0.6166 - 损失: 1.3343 - 前 5 名准确率: 0.9613 - 验证准确率: 0.6610 - 验证损失: 1.2695 - 验证前 5 名准确率: 0.9706
第 5 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 261ms/步 - 准确率: 0.6468 - 损失: 1.2814 - 前 5 名准确率: 0.9672 - 验证准确率: 0.6834 - 验证损失: 1.2231 - 验证前 5 名准确率: 0.9716
第 6 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 261ms/步 - 准确率: 0.6619 - 损失: 1.2412 - 前 5 名准确率: 0.9708 - 验证准确率: 0.6842 - 验证损失: 1.2018 - 验证前 5 名准确率: 0.9744
第 7 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 263ms/步 - 准确率: 0.6976 - 损失: 1.1775 - 前 5 名准确率: 0.9752 - 验证准确率: 0.6988 - 验证损失: 1.1988 - 验证前 5 名准确率: 0.9752
第 8 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 263ms/步 - 准确率: 0.7070 - 损失: 1.1579 - 前 5 名准确率: 0.9774 - 验证准确率: 0.7010 - 验证损失: 1.1780 - 验证前 5 名准确率: 0.9732
第 9 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 95s 269ms/步 - 准确率: 0.7219 - 损失: 1.1255 - 前 5 名准确率: 0.9795 - 验证准确率: 0.7166 - 验证损失: 1.1375 - 验证前 5 名准确率: 0.9784
第 10 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 264ms/步 - 准确率: 0.7273 - 损失: 1.1087 - 前 5 名准确率: 0.9801 - 验证准确率: 0.7258 - 验证损失: 1.1286 - 验证前 5 名准确率: 0.9814
第 11 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 265ms/步 - 准确率: 0.7361 - 损失: 1.0863 - 前 5 名准确率: 0.9828 - 验证准确率: 0.7222 - 验证损失: 1.1412 - 验证前 5 名准确率: 0.9766
第 12 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 264ms/步 - 准确率: 0.7504 - 损失: 1.0644 - 前 5 名准确率: 0.9834 - 验证准确率: 0.7418 - 验证损失: 1.0943 - 验证前 5 名准确率: 0.9812
第 13 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 94s 266ms/步 - 准确率: 0.7593 - 损失: 1.0422 - 前 5 名准确率: 0.9856 - 验证准确率: 0.7468 - 验证损失: 1.0834 - 验证前 5 名准确率: 0.9818
第 14 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 265ms/步 - 准确率: 0.7647 - 损失: 1.0307 - 前 5 名准确率: 0.9868 - 验证准确率: 0.7526 - 验证损失: 1.0863 - 验证前 5 名准确率: 0.9822
第 15 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 263ms/步 - 准确率: 0.7684 - 损失: 1.0231 - 前 5 名准确率: 0.9863 - 验证准确率: 0.7666 - 验证损失: 1.0454 - 验证前 5 名准确率: 0.9834
第 16 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 94s 268ms/步 - 准确率: 0.7809 - 损失: 1.0007 - 前 5 名准确率: 0.9859 - 验证准确率: 0.7670 - 验证损失: 1.0469 - 验证前 5 名准确率: 0.9838
第 17 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 94s 268ms/步 - 准确率: 0.7902 - 损失: 0.9795 - 前 5 名准确率: 0.9895 - 验证准确率: 0.7676 - 验证损失: 1.0396 - 验证前 5 名准确率: 0.9836
第 18 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 106s 301ms/步 - 准确率: 0.7920 - 损失: 0.9693 - 前 5 名准确率: 0.9889 - 验证准确率: 0.7616 - 验证损失: 1.0791 - 验证前 5 名准确率: 0.9828
第 19 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 264ms/步 - 准确率: 0.7965 - 损失: 0.9631 - 前 5 名准确率: 0.9893 - 验证准确率: 0.7850 - 验证损失: 1.0149 - 验证前 5 名准确率: 0.9842
第 20 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 265ms/步 - 准确率: 0.8030 - 损失: 0.9529 - 前 5 名准确率: 0.9899 - 验证准确率: 0.7898 - 验证损失: 1.0029 - 验证前 5 名准确率: 0.9852
第 21 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 261ms/步 - 准确率: 0.8118 - 损失: 0.9322 - 前 5 名准确率: 0.9903 - 验证准确率: 0.7728 - 验证损失: 1.0529 - 验证前 5 名准确率: 0.9850
第 22 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 91s 259ms/步 - 准确率: 0.8104 - 损失: 0.9308 - 前 5 名准确率: 0.9906 - 验证准确率: 0.7874 - 验证损失: 1.0090 - 验证前 5 名准确率: 0.9876
第 23 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 263ms/步 - 准确率: 0.8164 - 损失: 0.9193 - 前 5 名准确率: 0.9911 - 验证准确率: 0.7800 - 验证损失: 1.0091 - 验证前 5 名准确率: 0.9844
第 24 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 94s 268ms/步 - 准确率: 0.8147 - 损失: 0.9184 - 前 5 名准确率: 0.9919 - 验证准确率: 0.7854 - 验证损失: 1.0260 - 验证前 5 名准确率: 0.9856
第 25 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 262ms/步 - 准确率: 0.8255 - 损失: 0.9000 - 前 5 名准确率: 0.9914 - 验证准确率: 0.7918 - 验证损失: 1.0014 - 验证前 5 名准确率: 0.9842
第 26 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 90s 257ms/步 - 准确率: 0.8297 - 损失: 0.8865 - 前 5 名准确率: 0.9933 - 验证准确率: 0.7924 - 验证损失: 1.0065 - 验证前 5 名准确率: 0.9834
第 27 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 262ms/步 - 准确率: 0.8339 - 损失: 0.8837 - 前 5 名准确率: 0.9931 - 验证准确率: 0.7906 - 验证损失: 1.0035 - 验证前 5 名准确率: 0.9870
第 28 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 260ms/步 - 准确率: 0.8362 - 损失: 0.8781 - 前 5 名准确率: 0.9934 - 验证准确率: 0.7878 - 验证损失: 1.0041 - 验证前 5 名准确率: 0.9850
第 29 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 260ms/步 - 准确率: 0.8398 - 损失: 0.8707 - 前 5 名准确率: 0.9942 - 验证准确率: 0.7854 - 验证损失: 1.0186 - 验证前 5 名准确率: 0.9858
第 30 轮/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 263ms/步 - 准确率: 0.8438 - 损失: 0.8614 - 前 5 名准确率: 0.9933 - 验证准确率: 0.7892 - 验证损失: 1.0123 - 验证前 5 名准确率: 0.9846
313/313 ━━━━━━━━━━━━━━━━━━━━ 14s 44ms/步 - 准确率: 0.7752 - 损失: 1.0370 - 前 5 名准确率: 0.9824
测试准确率: 77.82%
测试前 5 名准确率: 98.42%
现在让我们可视化模型的训练进展。
plt.plot(history.history["loss"], label="train_loss") # 训练损失
plt.plot(history.history["val_loss"], label="val_loss") # 验证损失
plt.xlabel("Epochs") # 迭代周期
plt.ylabel("Loss") # 损失
plt.title("Train and Validation Losses Over Epochs", fontsize=14) # 训练和验证损失随迭代周期的变化
plt.legend()
plt.grid()
plt.show()
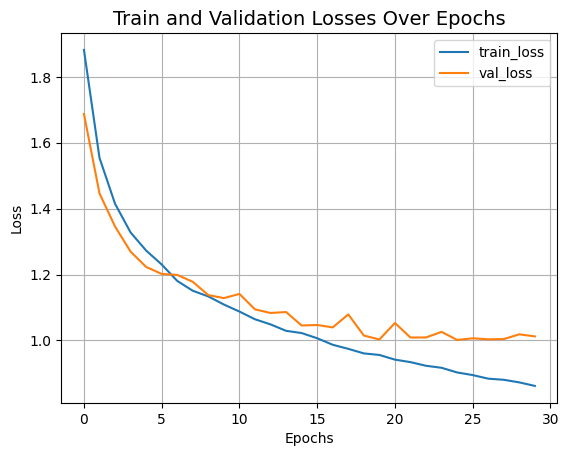
我们刚训练的CCT模型只有0.4百万个参数,并且在30个迭代周期内达到了大约79%的顶级准确率。上面的图表没有显示出过拟合的迹象。这意味着我们可以训练这个网络更长时间(也许再加上一些正则化),可能会获得更好的性能。这种性能还可以通过额外的方案进一步改善,如余弦衰减学习率调度、其他数据增强技术如AutoAugment、MixUp或Cutmix。通过这些修改,作者在CIFAR-10数据集上达到了95.1%的顶级准确率。作者还进行了多项实验,研究卷积块数量、变换器层数等如何影响CCT的最终性能。
作为对比,一个ViT模型约需要4.7百万个参数和100个迭代周期的训练才能在CIFAR-10数据集上达到78.22%的顶级准确率。您可以参考 这个笔记本 来了解实验设置。
作者还展示了紧凑卷积变换器在NLP任务上的性能,并报告了那里的竞争结果。
