► 代码示例 / 计算机视觉 / 增强型深度残差网络用于单幅图像超分辨率

增强型深度残差网络用于单幅图像超分辨率

作者: Gitesh Chawda
创建日期: 2022/04/07
最后修改: 2022/04/07
描述: 在DIV2K数据集上训练EDSR模型。

引言

在这个示例中，我们实现用于单幅图像超分辨率的增强型深度残差网络（EDSR）由Bee Lim、Sanghyun Son、Heewon Kim、Seungjun Nah和Kyoung Mu Lee提出。

EDSR架构基于SRResNet架构，由多个残差块组成。它使用常量缩放层而不是批归一化层，以产生一致的结果（输入和输出具有相似的分布，因此对中间特征进行归一化可能并不理想）。作者没有使用L2损失（均方误差），而是采用了L1损失（平均绝对误差），其在经验上表现更好。

我们的实现仅包括16个残差块和64个通道。

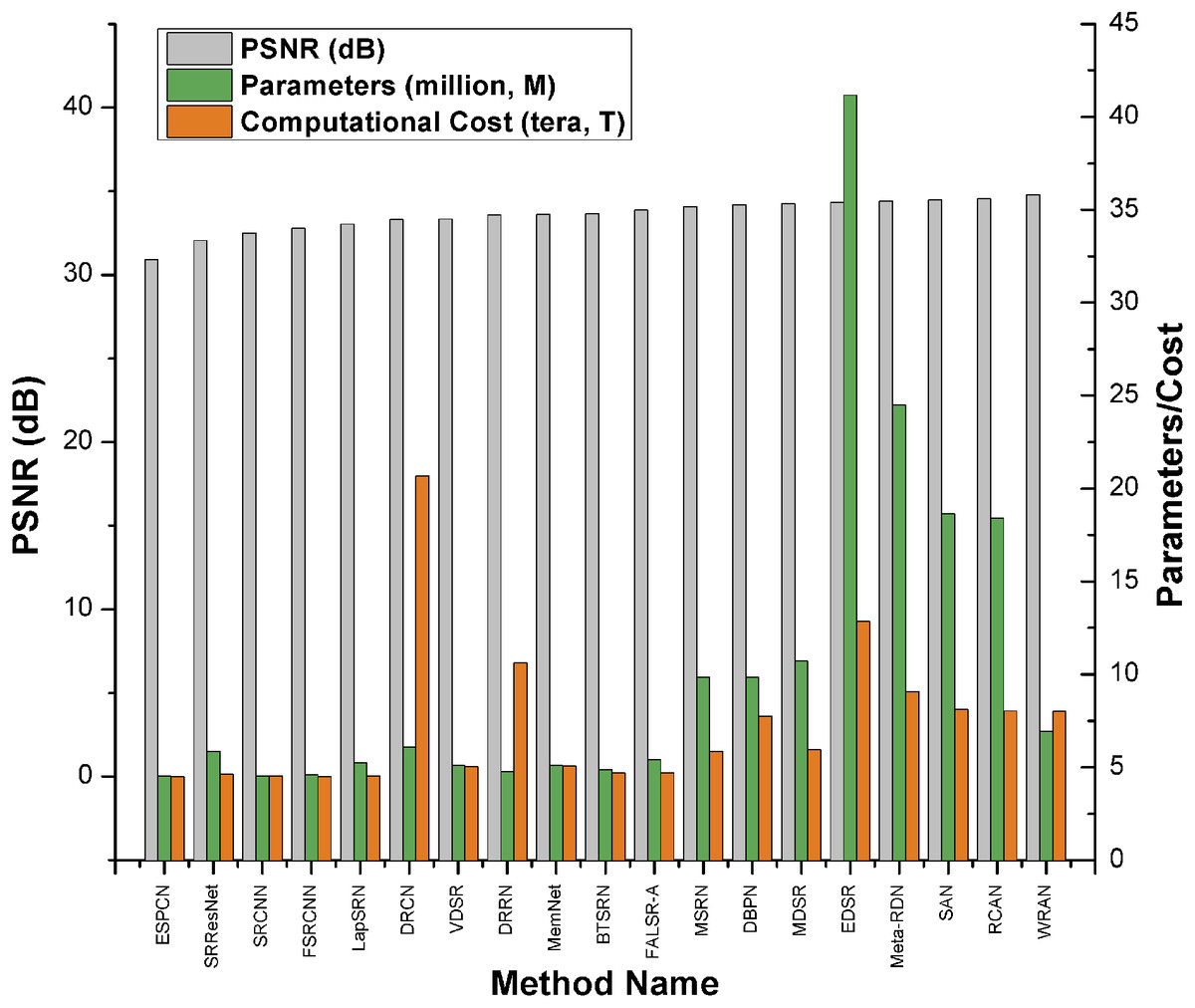
另外，如Keras示例所示使用有效的子像素CNN进行图像超分辨率，你可以使用ESPCN模型进行超分辨率。根据调查论文，EDSR是基于PSNR分数的前五种最佳超分辨率方法之一。然而，它比其他方法有更多参数并需要更多计算能力。它的PSNR值（≈34db）略高于ESPCN（≈32db）。根据调查论文，EDSR的表现优于ESPCN。

论文：基于深度学习的单幅图像超分辨率的全面评审

比较图：

导入库

import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
import matplotlib.pyplot as plt

from tensorflow import keras
from tensorflow.keras import layers

AUTOTUNE = tf.data.AUTOTUNE

下载训练数据集

我们使用DIV2K数据集，这是一个突出的单幅图像超分辨率数据集，包含1,000 张各种降质场景的图像，分为800张用于训练，100张用于验证，100张用于测试。我们使用4倍双三次下采样图像作为我们的“低质量”参考。

# 从TF数据集中下载DIV2K
# 使用双三次4倍降质类型
div2k_data = tfds.image.Div2k(config="bicubic_x4")
div2k_data.download_and_prepare()

# 从div2k_data对象获取训练数据
train = div2k_data.as_dataset(split="train", as_supervised=True)
train_cache = train.cache()
# 验证数据
val = div2k_data.as_dataset(split="validation", as_supervised=True)
val_cache = val.cache()

翻转、裁剪和调整图像大小

def flip_left_right(lowres_img, highres_img):
    """翻转图像左右。"""

    # 输出在 0 到 1 之间均匀分布的随机值
    rn = tf.random.uniform(shape=(), maxval=1)
    # 如果 rn 小于 0.5，返回原始 lowres_img 和 highres_img
    # 如果 rn 大于 0.5，返回翻转后的图像
    return tf.cond(
        rn < 0.5,
        lambda: (lowres_img, highres_img),
        lambda: (
            tf.image.flip_left_right(lowres_img),
            tf.image.flip_left_right(highres_img),
        ),
    )


def random_rotate(lowres_img, highres_img):
    """将图像旋转 90 度。"""

    # 输出在 0 到 4 之间均匀分布的随机值
    rn = tf.random.uniform(shape=(), maxval=4, dtype=tf.int32)
    # 这里 rn 表示图像旋转 90 度的次数
    return tf.image.rot90(lowres_img, rn), tf.image.rot90(highres_img, rn)


def random_crop(lowres_img, highres_img, hr_crop_size=96, scale=4):
    """裁剪图像。

    低分辨率图像：24x24
    高分辨率图像：96x96
    """
    lowres_crop_size = hr_crop_size // scale  # 96//4=24
    lowres_img_shape = tf.shape(lowres_img)[:2]  # (高度,宽度)

    lowres_width = tf.random.uniform(
        shape=(), maxval=lowres_img_shape[1] - lowres_crop_size + 1, dtype=tf.int32
    )
    lowres_height = tf.random.uniform(
        shape=(), maxval=lowres_img_shape[0] - lowres_crop_size + 1, dtype=tf.int32
    )

    highres_width = lowres_width * scale
    highres_height = lowres_height * scale

    lowres_img_cropped = lowres_img[
        lowres_height : lowres_height + lowres_crop_size,
        lowres_width : lowres_width + lowres_crop_size,
    ]  # 24x24
    highres_img_cropped = highres_img[
        highres_height : highres_height + hr_crop_size,
        highres_width : highres_width + hr_crop_size,
    ]  # 96x96

    return lowres_img_cropped, highres_img_cropped

准备一个 `tf.data.Dataset` 对象

我们用随机水平翻转和90度旋转增强训练数据。

作为低分辨率图像，我们使用24x24 RGB输入补丁。

def dataset_object(dataset_cache, training=True):

    ds = dataset_cache
    ds = ds.map(
        lambda lowres, highres: random_crop(lowres, highres, scale=4),
        num_parallel_calls=AUTOTUNE,
    )

    if training:
        ds = ds.map(random_rotate, num_parallel_calls=AUTOTUNE)
        ds = ds.map(flip_left_right, num_parallel_calls=AUTOTUNE)
    # 批量数据
    ds = ds.batch(16)

    if training:
        # 重复数据，以便数据集的基数变为无限
        ds = ds.repeat()
    # 预提取允许在当前图像处理的同时准备后续图像
    ds = ds.prefetch(buffer_size=AUTOTUNE)
    return ds


train_ds = dataset_object(train_cache, training=True)
val_ds = dataset_object(val_cache, training=False)

可视化数据

让我们可视化一些样本图像：

lowres, highres = next(iter(train_ds))

# 高分辨率图像
plt.figure(figsize=(10, 10))
for i in range(9):
    ax = plt.subplot(3, 3, i + 1)
    plt.imshow(highres[i].numpy().astype("uint8"))
    plt.title(highres[i].shape)
    plt.axis("off")

# 低分辨率图像
plt.figure(figsize=(10, 10))
for i in range(9):
    ax = plt.subplot(3, 3, i + 1)
    plt.imshow(lowres[i].numpy().astype("uint8"))
    plt.title(lowres[i].shape)
    plt.axis("off")


def PSNR(super_resolution, high_resolution):
    """计算峰值信噪比，衡量图像质量。"""
    # 像素的最大值为255
    psnr_value = tf.image.psnr(high_resolution, super_resolution, max_val=255)[0]
    return psnr_value

png

构建模型

在论文中，作者训练了三个模型：EDSR、MDSR和一个基线模型。在这个代码示例中，我们只训练基线模型。

与具有三个残差块的模型的比较

EDSR的残差块设计与ResNet不同。批量归一化层被移除（连同最终的ReLU激活）：由于批量归一化层会归一化特征，因此它们会影响输出值范围的灵活性。因此，最好将它们去除。此外，这也有助于减少模型所需的 GPU内存，因为批量归一化层消耗的内存与前面的卷积层相同。

class EDSRModel(tf.keras.Model):
    def train_step(self, data):
        # 解包数据。其结构取决于您的模型和
        # 您传递给 `fit()` 的内容。
        x, y = data

        with tf.GradientTape() as tape:
            y_pred = self(x, training=True)  # 前向传播
            # 计算损失值
            # (损失函数在 `compile()` 中配置)
            loss = self.compiled_loss(y, y_pred, regularization_losses=self.losses)

        # 计算梯度
        trainable_vars = self.trainable_variables
        gradients = tape.gradient(loss, trainable_vars)
        # 更新权重
        self.optimizer.apply_gradients(zip(gradients, trainable_vars))
        # 更新指标（包括跟踪损失的指标）
        self.compiled_metrics.update_state(y, y_pred)
        # 返回一个字典，将指标名称映射到当前值
        return {m.name: m.result() for m in self.metrics}

    def predict_step(self, x):
        # 使用 tf.expand_dims 添加虚拟维度并使用 tf.cast 转换为 float32
        x = tf.cast(tf.expand_dims(x, axis=0), tf.float32)
        # 将低分辨率图像传递给模型
        super_resolution_img = self(x, training=False)
        # 将张量限制在 min(0) 到 max(255) 之间
        super_resolution_img = tf.clip_by_value(super_resolution_img, 0, 255)
        # 将张量的值四舍五入到最接近的整数
        super_resolution_img = tf.round(super_resolution_img)
        # 从张量的形状中删除大小为 1 的维度并转换为 uint8
        super_resolution_img = tf.squeeze(
            tf.cast(super_resolution_img, tf.uint8), axis=0
        )
        return super_resolution_img


# 残差块
def ResBlock(inputs):
    x = layers.Conv2D(64, 3, padding="same", activation="relu")(inputs)
    x = layers.Conv2D(64, 3, padding="same")(x)
    x = layers.Add()([inputs, x])
    return x


# 上采样块
def Upsampling(inputs, factor=2, **kwargs):
    x = layers.Conv2D(64 * (factor ** 2), 3, padding="same", **kwargs)(inputs)
    x = tf.nn.depth_to_space(x, block_size=factor)
    x = layers.Conv2D(64 * (factor ** 2), 3, padding="same", **kwargs)(x)
    x = tf.nn.depth_to_space(x, block_size=factor)
    return x


def make_model(num_filters, num_of_residual_blocks):
    # 灵活的输入到输入层
    input_layer = layers.Input(shape=(None, None, 3))
    # 缩放像素值
    x = layers.Rescaling(scale=1.0 / 255)(input_layer)
    x = x_new = layers.Conv2D(num_filters, 3, padding="same")(x)

    # 16 个残差块
    for _ in range(num_of_residual_blocks):
        x_new = ResBlock(x_new)

    x_new = layers.Conv2D(num_filters, 3, padding="same")(x_new)
    x = layers.Add()([x, x_new])

    x = Upsampling(x)
    x = layers.Conv2D(3, 3, padding="same")(x)

    output_layer = layers.Rescaling(scale=255)(x)
    return EDSRModel(input_layer, output_layer)


model = make_model(num_filters=64, num_of_residual_blocks=16)

训练模型

# 使用adam优化器，初始学习率为1e-4，在5000步后将学习率改为5e-5
optim_edsr = keras.optimizers.Adam(
    learning_rate=keras.optimizers.schedules.PiecewiseConstantDecay(
        boundaries=[5000], values=[1e-4, 5e-5]
    )
)
# 用平均绝对误差（L1 Loss）作为损失，PSNR作为指标编译模型
model.compile(optimizer=optim_edsr, loss="mae", metrics=[PSNR])
# 训练更多轮次将改善结果
model.fit(train_ds, epochs=100, steps_per_epoch=200, validation_data=val_ds)

Epoch 1/100
200/200 [==============================] - 78s 322ms/step - loss: 27.7075 - PSNR: 19.4656 - val_loss: 14.7192 - val_PSNR: 22.5129
Epoch 2/100
200/200 [==============================] - 6s 28ms/step - loss: 12.6842 - PSNR: 24.7269 - val_loss: 12.4348 - val_PSNR: 22.8793
Epoch 3/100
200/200 [==============================] - 6s 28ms/step - loss: 10.7646 - PSNR: 27.3775 - val_loss: 10.6830 - val_PSNR: 24.9075
Epoch 4/100
200/200 [==============================] - 6s 28ms/step - loss: 9.8356 - PSNR: 27.4924 - val_loss: 9.2714 - val_PSNR: 27.7680
Epoch 5/100
200/200 [==============================] - 5s 27ms/step - loss: 9.1752 - PSNR: 29.4013 - val_loss: 8.7747 - val_PSNR: 27.6017
Epoch 6/100
200/200 [==============================] - 6s 30ms/step - loss: 8.8630 - PSNR: 27.8686 - val_loss: 8.7710 - val_PSNR: 30.2381
Epoch 7/100
200/200 [==============================] - 5s 27ms/step - loss: 8.7107 - PSNR: 28.4887 - val_loss: 8.3186 - val_PSNR: 29.4744
Epoch 8/100
200/200 [==============================] - 6s 32ms/step - loss: 8.5374 - PSNR: 28.9546 - val_loss: 8.4716 - val_PSNR: 28.8873
Epoch 9/100
200/200 [==============================] - 5s 27ms/step - loss: 8.4111 - PSNR: 30.2234 - val_loss: 8.1969 - val_PSNR: 28.9538
Epoch 10/100
200/200 [==============================] - 6s 28ms/step - loss: 8.3835 - PSNR: 29.7066 - val_loss: 8.9434 - val_PSNR: 31.9213
Epoch 11/100
200/200 [==============================] - 5s 27ms/step - loss: 8.1713 - PSNR: 30.7191 - val_loss: 8.2816 - val_PSNR: 30.7049
Epoch 12/100
200/200 [==============================] - 6s 30ms/step - loss: 7.9129 - PSNR: 30.3964 - val_loss: 8.9365 - val_PSNR: 26.2667
Epoch 13/100
200/200 [==============================] - 5s 27ms/step - loss: 8.2504 - PSNR: 30.1612 - val_loss: 7.8384 - val_PSNR: 28.4159
Epoch 14/100
200/200 [==============================] - 6s 31ms/step - loss: 8.0114 - PSNR: 30.2370 - val_loss: 7.2658 - val_PSNR: 29.4454
Epoch 15/100
200/200 [==============================] - 5s 27ms/step - loss: 8.0059 - PSNR: 30.7665 - val_loss: 7.6692 - val_PSNR: 31.8294
Epoch 16/100
200/200 [==============================] - 6s 28ms/step - loss: 7.9388 - PSNR: 30.5297 - val_loss: 7.7625 - val_PSNR: 28.6685
Epoch 17/100
200/200 [==============================] - 5s 27ms/step - loss: 7.8627 - PSNR: 30.8213 - val_loss: 8.1984 - val_PSNR: 30.9864
Epoch 18/100
200/200 [==============================] - 6s 30ms/step - loss: 7.8956 - PSNR: 30.4661 - val_loss: 8.2664 - val_PSNR: 34.1168
Epoch 19/100
200/200 [==============================] - 5s 27ms/step - loss: 7.7800 - PSNR: 30.3071 - val_loss: 7.9547 - val_PSNR: 30.9254
Epoch 20/100
200/200 [==============================] - 6s 31ms/step - loss: 7.7402 - PSNR: 30.7251 - val_loss: 7.9632 - val_PSNR: 31.7438
Epoch 21/100
200/200 [==============================] - 5s 27ms/step - loss: 7.7372 - PSNR: 31.3348 - val_loss: 8.0512 - val_PSNR: 29.4988
Epoch 22/100
200/200 [==============================] - 6s 28ms/step - loss: 7.7207 - PSNR: 31.1984 - val_loss: 7.6072 - val_PSNR: 32.6720
Epoch 23/100
200/200 [==============================] - 6s 29ms/step - loss: 7.5955 - PSNR: 31.3128 - val_loss: 6.8593 - val_PSNR: 28.1123
Epoch 24/100
200/200 [==============================] - 6s 28ms/step - loss: 7.6341 - PSNR: 31.6670 - val_loss: 7.4485 - val_PSNR: 30.0567
Epoch 25/100
200/200 [==============================] - 6s 28ms/step - loss: 7.5404 - PSNR: 31.5332 - val_loss: 6.8795 - val_PSNR: 33.6179
Epoch 26/100
200/200 [==============================] - 6s 31ms/step - loss: 7.4429 - PSNR: 32.3681 - val_loss: 7.5937 - val_PSNR: 32.5076
Epoch 27/100
200/200 [==============================] - 6s 28ms/step - loss: 7.4243 - PSNR: 31.2899 - val_loss: 7.0982 - val_PSNR: 37.4561
Epoch 28/100
200/200 [==============================] - 5s 27ms/step - loss: 7.3542 - PSNR: 31.3620 - val_loss: 7.5735 - val_PSNR: 29.3892
Epoch 29/100
200/200 [==============================] - 6s 31ms/step - loss: 7.2648 - PSNR: 32.0806 - val_loss: 7.7589 - val_PSNR: 28.5829
Epoch 30/100
200/200 [==============================] - 5s 27ms/step - loss: 7.2954 - PSNR: 32.3495 - val_loss: 7.1625 - val_PSNR: 32.0560
Epoch 31/100
200/200 [==============================] - 6s 31ms/step - loss: 7.4815 - PSNR: 32.3662 - val_loss: 7.8601 - val_PSNR: 35.0962
Epoch 32/100
200/200 [==============================] - 6s 29ms/step - loss: 7.3957 - PSNR: 30.4455 - val_loss: 7.4800 - val_PSNR: 31.9397
Epoch 33/100
200/200 [==============================] - 6s 29ms/step - loss: 7.3849 - PSNR: 32.0058 - val_loss: 7.2225 - val_PSNR: 35.5276
Epoch 34/100
200/200 [==============================] - 6s 28ms/step - loss: 7.4285 - PSNR: 31.6806 - val_loss: 7.3937 - val_PSNR: 30.4433
Epoch 35/100
200/200 [==============================] - 6s 30ms/step - loss: 7.3841 - PSNR: 32.1425 - val_loss: 7.6458 - val_PSNR: 30.7912
Epoch 36/100
200/200 [==============================] - 5s 27ms/step - loss: 7.3049 - PSNR: 31.7272 - val_loss: 7.5190 - val_PSNR: 33.2980
Epoch 37/100
200/200 [==============================] - 6s 31ms/step - loss: 7.3098 - PSNR: 31.7727 - val_loss: 8.0041 - val_PSNR: 26.8507
Epoch 38/100
200/200 [==============================] - 6s 28ms/step - loss: 7.4027 - PSNR: 31.1814 - val_loss: 7.7334 - val_PSNR: 29.2905
Epoch 39/100
200/200 [==============================] - 6s 29ms/step - loss: 7.2470 - PSNR: 31.3636 - val_loss: 7.1275 - val_PSNR: 33.1772
Epoch 40/100
200/200 [==============================] - 6s 28ms/step - loss: 7.1907 - PSNR: 32.7381 - val_loss: 7.3437 - val_PSNR: 33.7216
Epoch 41/100
200/200 [==============================] - 6s 29ms/step - loss: 7.3383 - PSNR: 31.6409 - val_loss: 6.8769 - val_PSNR: 29.9654
Epoch 42/100
200/200 [==============================] - 5s 27ms/step - loss: 7.3393 - PSNR: 31.4941 - val_loss: 6.1088 - val_PSNR: 35.7083
Epoch 43/100
200/200 [==============================] - 6s 32ms/step - loss: 7.2272 - PSNR: 32.2356 - val_loss: 7.4534 - val_PSNR: 29.5734
Epoch 44/100
200/200 [==============================] - 6s 30ms/step - loss: 7.1773 - PSNR: 32.0016 - val_loss: 7.4676 - val_PSNR: 33.0795
Epoch 45/100
200/200 [==============================] - 6s 28ms/step - loss: 7.4677 - PSNR: 32.3508 - val_loss: 7.2459 - val_PSNR: 31.6806
Epoch 46/100
200/200 [==============================] - 6s 30ms/step - loss: 7.2347 - PSNR: 33.3392 - val_loss: 7.0098 - val_PSNR: 27.1658
Epoch 47/100
200/200 [==============================] - 6s 28ms/step - loss: 7.4494 - PSNR: 32.1602 - val_loss: 8.0211 - val_PSNR: 29.9740
Epoch 48/100
200/200 [==============================] - 6s 28ms/step - loss: 7.1128 - PSNR: 32.1696 - val_loss: 7.0101 - val_PSNR: 32.8874
Epoch 49/100
200/200 [==============================] - 6s 31ms/step - loss: 7.1698 - PSNR: 32.0733 - val_loss: 7.5813 - val_PSNR: 26.1697
Epoch 50/100
200/200 [==============================] - 6s 30ms/step - loss: 7.1904 - PSNR: 31.9198 - val_loss: 6.3655 - val_PSNR: 33.4935
Epoch 51/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0957 - PSNR: 32.3727 - val_loss: 7.2626 - val_PSNR: 28.8388
Epoch 52/100
200/200 [==============================] - 6s 30ms/step - loss: 7.1436 - PSNR: 32.2141 - val_loss: 7.6012 - val_PSNR: 31.2261
Epoch 53/100
200/200 [==============================] - 6s 28ms/step - loss: 7.2270 - PSNR: 32.2675 - val_loss: 6.9826 - val_PSNR: 27.6408
Epoch 54/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0638 - PSNR: 32.5191 - val_loss: 6.6046 - val_PSNR: 32.3862
Epoch 55/100
200/200 [==============================] - 6s 31ms/step - loss: 7.1609 - PSNR: 31.6787 - val_loss: 7.3563 - val_PSNR: 28.3834
Epoch 56/100
200/200 [==============================] - 6s 30ms/step - loss: 7.1953 - PSNR: 31.9948 - val_loss: 6.5111 - val_PSNR: 34.0409
Epoch 57/100
200/200 [==============================] - 6s 30ms/step - loss: 7.1168 - PSNR: 32.3288 - val_loss: 6.7979 - val_PSNR: 31.8126
Epoch 58/100
200/200 [==============================] - 6s 29ms/step - loss: 7.0578 - PSNR: 33.1605 - val_loss: 6.8349 - val_PSNR: 32.0840
Epoch 59/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0890 - PSNR: 32.7020 - val_loss: 7.4109 - val_PSNR: 31.8377
Epoch 60/100
200/200 [==============================] - 6s 29ms/step - loss: 7.1357 - PSNR: 32.9600 - val_loss: 7.7647 - val_PSNR: 30.2965
Epoch 61/100
200/200 [==============================] - 6s 32ms/step - loss: 7.2003 - PSNR: 32.0152 - val_loss: 7.8508 - val_PSNR: 27.8501
Epoch 62/100
200/200 [==============================] - 6s 30ms/step - loss: 7.0474 - PSNR: 32.4485 - val_loss: 7.3319 - val_PSNR: 28.4571
Epoch 63/100
200/200 [==============================] - 6s 30ms/step - loss: 7.1315 - PSNR: 32.6996 - val_loss: 7.0695 - val_PSNR: 34.9915
Epoch 64/100
200/200 [==============================] - 6s 28ms/step - loss: 7.1181 - PSNR: 32.9488 - val_loss: 6.2144 - val_PSNR: 33.9663
Epoch 65/100
200/200 [==============================] - 6s 29ms/step - loss: 7.1262 - PSNR: 32.0699 - val_loss: 7.1910 - val_PSNR: 34.1321
Epoch 66/100
200/200 [==============================] - 6s 28ms/step - loss: 7.2891 - PSNR: 32.5745 - val_loss: 6.9004 - val_PSNR: 34.5732
Epoch 67/100
200/200 [==============================] - 6s 31ms/step - loss: 6.8185 - PSNR: 32.2085 - val_loss: 6.8353 - val_PSNR: 27.2619
Epoch 68/100
200/200 [==============================] - 7s 33ms/step - loss: 6.9238 - PSNR: 33.3510 - val_loss: 7.3350 - val_PSNR: 28.2281
Epoch 69/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0037 - PSNR: 31.6955 - val_loss: 6.5887 - val_PSNR: 30.3138
Epoch 70/100
200/200 [==============================] - 5s 27ms/step - loss: 7.0239 - PSNR: 32.6923 - val_loss: 6.6467 - val_PSNR: 36.0194
Epoch 71/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0828 - PSNR: 32.0297 - val_loss: 6.5626 - val_PSNR: 34.4241
Epoch 72/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0717 - PSNR: 32.5201 - val_loss: 7.5056 - val_PSNR: 31.4176
Epoch 73/100
200/200 [==============================] - 6s 29ms/step - loss: 7.0943 - PSNR: 32.4469 - val_loss: 7.0981 - val_PSNR: 33.2052
Epoch 74/100
200/200 [==============================] - 8s 38ms/step - loss: 7.0288 - PSNR: 32.2301 - val_loss: 6.9661 - val_PSNR: 34.0108
Epoch 75/100
200/200 [==============================] - 6s 28ms/step - loss: 7.1122 - PSNR: 32.1658 - val_loss: 6.9569 - val_PSNR: 30.8972
Epoch 76/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0108 - PSNR: 31.5408 - val_loss: 7.1185 - val_PSNR: 26.8445
Epoch 77/100
200/200 [==============================] - 6s 28ms/step - loss: 6.7812 - PSNR: 32.4927 - val_loss: 7.0030 - val_PSNR: 31.6901
Epoch 78/100
200/200 [==============================] - 6s 29ms/step - loss: 6.9885 - PSNR: 31.9727 - val_loss: 7.1126 - val_PSNR: 29.0163
Epoch 79/100
200/200 [==============================] - 6s 30ms/step - loss: 7.0738 - PSNR: 32.4997 - val_loss: 6.7849 - val_PSNR: 31.0740
Epoch 80/100
200/200 [==============================] - 6s 29ms/step - loss: 7.0899 - PSNR: 31.7940 - val_loss: 6.9975 - val_PSNR: 33.6309
Epoch 81/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0215 - PSNR: 32.6563 - val_loss: 6.5724 - val_PSNR: 35.1765
Epoch 82/100
200/200 [==============================] - 6s 28ms/step - loss: 6.9076 - PSNR: 32.9912 - val_loss: 6.8611 - val_PSNR: 31.8409
Epoch 83/100
200/200 [==============================] - 6s 28ms/step - loss: 6.9978 - PSNR: 32.7159 - val_loss: 6.4787 - val_PSNR: 31.5799
Epoch 84/100
200/200 [==============================] - 6s 29ms/step - loss: 7.1276 - PSNR: 32.8232 - val_loss: 7.9006 - val_PSNR: 27.5171
Epoch 85/100
200/200 [==============================] - 7s 33ms/step - loss: 7.0276 - PSNR: 32.3290 - val_loss: 8.5374 - val_PSNR: 25.2824
Epoch 86/100
200/200 [==============================] - 7s 33ms/step - loss: 7.0434 - PSNR: 31.4983 - val_loss: 6.9392 - val_PSNR: 35.9229
Epoch 87/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0703 - PSNR: 32.2641 - val_loss: 7.8662 - val_PSNR: 28.1676
Epoch 88/100
200/200 [==============================] - 6s 28ms/step - loss: 7.1311 - PSNR: 32.2141 - val_loss: 7.2089 - val_PSNR: 27.3218
Epoch 89/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0730 - PSNR: 33.3360 - val_loss: 6.7915 - val_PSNR: 29.1367
Epoch 90/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0177 - PSNR: 32.6117 - val_loss: 8.3779 - val_PSNR: 31.9831
Epoch 91/100
200/200 [==============================] - 6s 31ms/step - loss: 6.9638 - PSNR: 32.2765 - val_loss: 6.6582 - val_PSNR: 37.5391
Epoch 92/100
200/200 [==============================] - 6s 28ms/step - loss: 6.9623 - PSNR: 32.8864 - val_loss: 7.7435 - val_PSNR: 29.8939
Epoch 93/100
200/200 [==============================] - 6s 29ms/step - loss: 6.8474 - PSNR: 32.5345 - val_loss: 6.8181 - val_PSNR: 28.1166
Epoch 94/100
200/200 [==============================] - 6s 28ms/step - loss: 6.9059 - PSNR: 32.0613 - val_loss: 7.0014 - val_PSNR: 33.2055
Epoch 95/100
200/200 [==============================] - 6s 29ms/step - loss: 7.0418 - PSNR: 32.2906 - val_loss: 6.9686 - val_PSNR: 28.8045
Epoch 96/100
200/200 [==============================] - 6s 30ms/step - loss: 6.8624 - PSNR: 32.5043 - val_loss: 7.2015 - val_PSNR: 33.2103
Epoch 97/100
200/200 [==============================] - 7s 33ms/step - loss: 6.9632 - PSNR: 33.0834 - val_loss: 7.0972 - val_PSNR: 30.3407
Epoch 98/100
200/200 [==============================] - 6s 31ms/step - loss: 6.9307 - PSNR: 31.9062 - val_loss: 7.3421 - val_PSNR: 31.5380
Epoch 99/100
200/200 [==============================] - 6s 28ms/step - loss: 7.0685 - PSNR: 31.9839 - val_loss: 7.9828 - val_PSNR: 33.0619
Epoch 100/100
200/200 [==============================] - 6s 28ms/step - loss: 6.9233 - PSNR: 31.8346 - val_loss: 6.3802 - val_PSNR: 38.4415

<keras.callbacks.History at 0x7fe3682f2c90>

在新图像上运行推理并绘制结果

def plot_results(lowres, preds):
    """
    显示低分辨率图像和超分辨率图像
    """
    plt.figure(figsize=(24, 14))
    plt.subplot(132), plt.imshow(lowres), plt.title("低分辨率")
    plt.subplot(133), plt.imshow(preds), plt.title("预测")
    plt.show()


for lowres, highres in val.take(10):
    lowres = tf.image.random_crop(lowres, (150, 150, 3))
    preds = model.predict_step(lowres)
    plot_results(lowres, preds)