用自动编码器进行遮蔽图像建模
作者: Aritra Roy Gosthipaty, Sayak Paul
创建日期: 2021/12/20
最后修改: 2021/12/21
说明: 实现用于自监督预训练的遮蔽自动编码器。
引言
在深度学习中,具有不断增长的容量和能力的模型很容易在大型数据集(ImageNet-1K)上过拟合。在自然语言处理领域,对于数据的需求已通过自监督预训练得到了成功解决。
在He等人发表的学术论文 Masked Autoencoders Are Scalable Vision Learners中,作者提出了一种简单而有效的方法来预训练大型视觉模型(此处为ViT Huge)。受BERT预训练算法(Devlin等)的启发,他们对图像进行遮蔽,且通过自动编码器预测遮蔽的图像块。按照“遮蔽语言建模”的精神,这一预训练任务可以称为“遮蔽图像建模”。
在这个示例中,我们实现 Masked Autoencoders Are Scalable Vision Learners 使用CIFAR-10数据集。在预训练一个缩小版本的ViT之后,我们还实现了CIFAR-10上的线性评估流程。
此实现涵盖(MAE指遮蔽自动编码器):
- 遮蔽算法
- MAE编码器
- MAE解码器
- 使用线性探测进行评估
作为参考,我们重用了 这个示例中展示的一些代码。
导入
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import tensorflow as tf
import keras
from keras import layers
import matplotlib.pyplot as plt
import numpy as np
import random
# 设置种子以确保可重复性。
SEED = 42
keras.utils.set_random_seed(SEED)
预训练的超参数
请随意更改超参数并检查您的结果。获取架构直观的最佳方法是进行实验。我们的超参数受到作者在 原始论文中提出的设计指南的极大启发。
# 数据
BUFFER_SIZE = 1024
BATCH_SIZE = 256
AUTO = tf.data.AUTOTUNE
INPUT_SHAPE = (32, 32, 3)
NUM_CLASSES = 10
# 优化器
LEARNING_RATE = 5e-3
WEIGHT_DECAY = 1e-4
# 预训练
EPOCHS = 100
# 增强
IMAGE_SIZE = 48 # 我们将把输入图像调整为这个大小。
PATCH_SIZE = 6 # 从输入图像中提取的图像块大小。
NUM_PATCHES = (IMAGE_SIZE // PATCH_SIZE) ** 2
MASK_PROPORTION = 0.75 # 我们发现75%的遮蔽能给我们最佳结果。
# 编码器和解码器
LAYER_NORM_EPS = 1e-6
ENC_PROJECTION_DIM = 128
DEC_PROJECTION_DIM = 64
ENC_NUM_HEADS = 4
ENC_LAYERS = 6
DEC_NUM_HEADS = 4
DEC_LAYERS = (
2 # 解码器是轻量级的,但对于重建来说应该相当深入。
)
ENC_TRANSFORMER_UNITS = [
ENC_PROJECTION_DIM * 2,
ENC_PROJECTION_DIM,
] # 变换器层的大小。
DEC_TRANSFORMER_UNITS = [
DEC_PROJECTION_DIM * 2,
DEC_PROJECTION_DIM,
]
加载并准备CIFAR-10数据集
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
(x_train, y_train), (x_val, y_val) = (
(x_train[:40000], y_train[:40000]),
(x_train[40000:], y_train[40000:]),
)
print(f"训练样本: {len(x_train)}")
print(f"验证样本: {len(x_val)}")
print(f"测试样本: {len(x_test)}")
train_ds = tf.data.Dataset.from_tensor_slices(x_train)
train_ds = train_ds.shuffle(BUFFER_SIZE).batch(BATCH_SIZE).prefetch(AUTO)
val_ds = tf.data.Dataset.from_tensor_slices(x_val)
val_ds = val_ds.batch(BATCH_SIZE).prefetch(AUTO)
test_ds = tf.data.Dataset.from_tensor_slices(x_test)
test_ds = test_ds.batch(BATCH_SIZE).prefetch(AUTO)
训练样本: 40000
验证样本: 10000
测试样本: 10000
数据增强
在以往的自监督预训练方法中 (类似于SimCLR),我们注意到数据增强管道发挥了重要作用。另一方面,本文的作者指出,遮蔽自动编码器不依赖于增强。他们提出了一个简单的增强管道:
- 调整大小
- 随机裁剪(固定大小或随机大小)
- 随机水平翻转
def get_train_augmentation_model():
model = keras.Sequential(
[
layers.Rescaling(1 / 255.0),
layers.Resizing(INPUT_SHAPE[0] + 20, INPUT_SHAPE[0] + 20),
layers.RandomCrop(IMAGE_SIZE, IMAGE_SIZE),
layers.RandomFlip("horizontal"),
],
name="train_data_augmentation",
)
return model
def get_test_augmentation_model():
model = keras.Sequential(
[
layers.Rescaling(1 / 255.0),
layers.Resizing(IMAGE_SIZE, IMAGE_SIZE),
],
name="test_data_augmentation",
)
return model
用于从图像中提取补丁的层
该层将图像作为输入并将它们划分为补丁。该层还包括 两个实用方法:
show_patched_image– 接受一批图像及其对应的补丁以绘制随机的一对图像和补丁。reconstruct_from_patch– 接受一个补丁的单个实例并将它们缝合 回原始图像。
class Patches(layers.Layer):
def __init__(self, patch_size=PATCH_SIZE, **kwargs):
super().__init__(**kwargs)
self.patch_size = patch_size
# 假设图像有三个通道,每个补丁的大小将是
# (patch_size, patch_size, 3)。
self.resize = layers.Reshape((-1, patch_size * patch_size * 3))
def call(self, images):
# 从输入图像创建补丁
patches = tf.image.extract_patches(
images=images,
sizes=[1, self.patch_size, self.patch_size, 1],
strides=[1, self.patch_size, self.patch_size, 1],
rates=[1, 1, 1, 1],
padding="VALID",
)
# 将补丁重塑为 (batch, num_patches, patch_area) 并返回。
patches = self.resize(patches)
return patches
def show_patched_image(self, images, patches):
# 这是一个实用函数,接受一批图像及其
# 相应的补丁并帮助可视化一幅图像及其补丁
# 并排显示。
idx = np.random.choice(patches.shape[0])
print(f"选择的索引: {idx}.")
plt.figure(figsize=(4, 4))
plt.imshow(keras.utils.array_to_img(images[idx]))
plt.axis("off")
plt.show()
n = int(np.sqrt(patches.shape[1]))
plt.figure(figsize=(4, 4))
for i, patch in enumerate(patches[idx]):
ax = plt.subplot(n, n, i + 1)
patch_img = tf.reshape(patch, (self.patch_size, self.patch_size, 3))
plt.imshow(keras.utils.img_to_array(patch_img))
plt.axis("off")
plt.show()
# 返回选择的索引,以便在方法外进行验证。
return idx
# 来源于 https://stackoverflow.com/a/58082878/10319735
def reconstruct_from_patch(self, patch):
# 这个实用函数从一个*单一*图像中提取补丁并
# 将其重建回图像。这对于训练
# 监控回调非常有用。
num_patches = patch.shape[0]
n = int(np.sqrt(num_patches))
patch = tf.reshape(patch, (num_patches, self.patch_size, self.patch_size, 3))
rows = tf.split(patch, n, axis=0)
rows = [tf.concat(tf.unstack(x), axis=1) for x in rows]
reconstructed = tf.concat(rows, axis=0)
return reconstructed
让我们可视化图像补丁。
# 获取一批图像。
image_batch = next(iter(train_ds))
# 增强图像。
augmentation_model = get_train_augmentation_model()
augmented_images = augmentation_model(image_batch)
# 定义补丁层。
patch_layer = Patches()
# 从批量图像中获取补丁。
patches = patch_layer(images=augmented_images)
# 现在将图像和相应的补丁
# 传递给 `show_patched_image` 方法。
random_index = patch_layer.show_patched_image(images=augmented_images, patches=patches)
# 选择相同的图像并尝试将补丁重建
# 回原始图像。
image = patch_layer.reconstruct_from_patch(patches[random_index])
plt.imshow(image)
plt.axis("off")
plt.show()
选择的索引: 102.



带掩码的补丁编码
引用论文
类似于ViT,我们将图像划分为规则的非重叠补丁。然后我们抽取 一个补丁的子集并掩盖(即,移除)其余部分。我们的抽样策略是 简单明了:我们在不放回的情况下随机抽取补丁,遵循均匀 分布。我们将其简单称为“随机抽样”。 该层包括对补丁的掩码和编码。
该层的实用方法有:
get_random_indices– 提供掩码和未掩码索引。generate_masked_image– 采用补丁和未掩码索引,生成一个随机掩码图像。这个方法是我们训练监控回调的一个重要实用工具(将在后面定义)。
class PatchEncoder(layers.Layer):
def __init__(
self,
patch_size=PATCH_SIZE,
projection_dim=ENC_PROJECTION_DIM,
mask_proportion=MASK_PROPORTION,
downstream=False,
**kwargs,
):
super().__init__(**kwargs)
self.patch_size = patch_size
self.projection_dim = projection_dim
self.mask_proportion = mask_proportion
self.downstream = downstream
# 这是一个可训练的掩码令牌,随机初始化来自正态
# 分布。
self.mask_token = tf.Variable(
tf.random.normal([1, patch_size * patch_size * 3]), trainable=True
)
def build(self, input_shape):
(_, self.num_patches, self.patch_area) = input_shape
# 为补丁创建投影层。
self.projection = layers.Dense(units=self.projection_dim)
# 创建位置嵌入层。
self.position_embedding = layers.Embedding(
input_dim=self.num_patches, output_dim=self.projection_dim
)
# 将被掩罩的补丁数量。
self.num_mask = int(self.mask_proportion * self.num_patches)
def call(self, patches):
# 获取位置嵌入。
batch_size = tf.shape(patches)[0]
positions = tf.range(start=0, limit=self.num_patches, delta=1)
pos_embeddings = self.position_embedding(positions[tf.newaxis, ...])
pos_embeddings = tf.tile(
pos_embeddings, [batch_size, 1, 1]
) # (B, num_patches, projection_dim)
# 嵌入补丁。
patch_embeddings = (
self.projection(patches) + pos_embeddings
) # (B, num_patches, projection_dim)
if self.downstream:
return patch_embeddings
else:
mask_indices, unmask_indices = self.get_random_indices(batch_size)
# 编码器输入是未掩罩的补丁嵌入。这里我们收集
# 所有应该未掩罩的补丁。
unmasked_embeddings = tf.gather(
patch_embeddings, unmask_indices, axis=1, batch_dims=1
) # (B, unmask_numbers, projection_dim)
# 获取未掩罩和掩罩的位置嵌入。我们将需要它们
# 用于解码器。
unmasked_positions = tf.gather(
pos_embeddings, unmask_indices, axis=1, batch_dims=1
) # (B, unmask_numbers, projection_dim)
masked_positions = tf.gather(
pos_embeddings, mask_indices, axis=1, batch_dims=1
) # (B, mask_numbers, projection_dim)
# 重复掩码令牌数量倍数的掩码次数。
# 掩码令牌替换图像的掩码。
mask_tokens = tf.repeat(self.mask_token, repeats=self.num_mask, axis=0)
mask_tokens = tf.repeat(
mask_tokens[tf.newaxis, ...], repeats=batch_size, axis=0
)
# 获取令牌的掩码嵌入。
masked_embeddings = self.projection(mask_tokens) + masked_positions
return (
unmasked_embeddings, # 输入到编码器中。
masked_embeddings, # 输入到解码器的第一部分。
unmasked_positions, # 添加到编码器输出中。
mask_indices, # 被掩罩的索引。
unmask_indices, # 被未掩罩的索引。
)
def get_random_indices(self, batch_size):
# 从均匀分布创建随机索引,然后将其拆分
# 成掩码和未掩码索引。
rand_indices = tf.argsort(
tf.random.uniform(shape=(batch_size, self.num_patches)), axis=-1
)
mask_indices = rand_indices[:, : self.num_mask]
unmask_indices = rand_indices[:, self.num_mask :]
return mask_indices, unmask_indices
def generate_masked_image(self, patches, unmask_indices):
# 选择一个随机补丁及其对应的未掩码索引。
idx = np.random.choice(patches.shape[0])
patch = patches[idx]
unmask_index = unmask_indices[idx]
# 构建一个与补丁形状相同的numpy数组。
new_patch = np.zeros_like(patch)
# 遍历new_patch并插入未掩罩的补丁。
count = 0
for i in range(unmask_index.shape[0]):
new_patch[unmask_index[i]] = patch[unmask_index[i]]
return new_patch, idx
让我们看看在样本图像上的掩罩过程如何进行。
# 创建补丁编码层。
patch_encoder = PatchEncoder()
# 获取嵌入和位置。
(
unmasked_embeddings,
masked_embeddings,
unmasked_positions,
mask_indices,
unmask_indices,
) = patch_encoder(patches=patches)
# 显示一个已遮罩的补丁图像。
new_patch, random_index = patch_encoder.generate_masked_image(patches, unmask_indices)
plt.figure(figsize=(10, 10))
plt.subplot(1, 2, 1)
img = patch_layer.reconstruct_from_patch(new_patch)
plt.imshow(keras.utils.array_to_img(img))
plt.axis("off")
plt.title("已遮罩")
plt.subplot(1, 2, 2)
img = augmented_images[random_index]
plt.imshow(keras.utils.array_to_img(img))
plt.axis("off")
plt.title("原始")
plt.show()

MLP
这作为变压器架构的全连接前馈网络。
def mlp(x, dropout_rate, hidden_units):
for units in hidden_units:
x = layers.Dense(units, activation=tf.nn.gelu)(x)
x = layers.Dropout(dropout_rate)(x)
return x
MAE 编码器
MAE 编码器是 ViT。唯一需要注意的一点是编码器输出经过层归一化的输出。
def create_encoder(num_heads=ENC_NUM_HEADS, num_layers=ENC_LAYERS):
inputs = layers.Input((None, ENC_PROJECTION_DIM))
x = inputs
for _ in range(num_layers):
# 层归一化 1.
x1 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x)
# 创建一个多头注意力层。
attention_output = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=ENC_PROJECTION_DIM, dropout=0.1
)(x1, x1)
# 跳跃连接 1.
x2 = layers.Add()([attention_output, x])
# 层归一化 2.
x3 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x2)
# MLP.
x3 = mlp(x3, hidden_units=ENC_TRANSFORMER_UNITS, dropout_rate=0.1)
# 跳跃连接 2.
x = layers.Add()([x3, x2])
outputs = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x)
return keras.Model(inputs, outputs, name="mae_encoder")
MAE 解码器
作者指出他们使用的是一种非对称自编码器模型。他们使用一个轻量级解码器,每个令牌的计算量"<10%"相对于编码器。我们在实现中并未具体说明"<10%计算",但使用了一个较小的解码器(在深度和投影维度上均较小)。
def create_decoder(
num_layers=DEC_LAYERS, num_heads=DEC_NUM_HEADS, image_size=IMAGE_SIZE
):
inputs = layers.Input((NUM_PATCHES, ENC_PROJECTION_DIM))
x = layers.Dense(DEC_PROJECTION_DIM)(inputs)
for _ in range(num_layers):
# 层归一化 1.
x1 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x)
# 创建一个多头注意力层。
attention_output = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=DEC_PROJECTION_DIM, dropout=0.1
)(x1, x1)
# 跳跃连接 1.
x2 = layers.Add()([attention_output, x])
# 层归一化 2.
x3 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x2)
# MLP.
x3 = mlp(x3, hidden_units=DEC_TRANSFORMER_UNITS, dropout_rate=0.1)
# 跳跃连接 2.
x = layers.Add()([x3, x2])
x = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x)
x = layers.Flatten()(x)
pre_final = layers.Dense(units=image_size * image_size * 3, activation="sigmoid")(x)
outputs = layers.Reshape((image_size, image_size, 3))(pre_final)
return keras.Model(inputs, outputs, name="mae_decoder")
MAE 训练器
这是训练模块。我们将编码器和解码器封装在一个 tf.keras.Model 子类中。这允许我们定制 model.fit() 循环中发生的事情。
class MaskedAutoencoder(keras.Model):
def __init__(
self,
train_augmentation_model,
test_augmentation_model,
patch_layer,
patch_encoder,
encoder,
decoder,
**kwargs,
):
super().__init__(**kwargs)
self.train_augmentation_model = train_augmentation_model
self.test_augmentation_model = test_augmentation_model
self.patch_layer = patch_layer
self.patch_encoder = patch_encoder
self.encoder = encoder
self.decoder = decoder
def calculate_loss(self, images, test=False):
# 增强输入图像。
if test:
augmented_images = self.test_augmentation_model(images)
else:
augmented_images = self.train_augmentation_model(images)
# 对增强后的图像进行切片。
patches = self.patch_layer(augmented_images)
# 编码切片。
(
unmasked_embeddings,
masked_embeddings,
unmasked_positions,
mask_indices,
unmask_indices,
) = self.patch_encoder(patches)
# 将未遮盖的切片传递给编码器。
encoder_outputs = self.encoder(unmasked_embeddings)
# 创建解码器输入。
encoder_outputs = encoder_outputs + unmasked_positions
decoder_inputs = tf.concat([encoder_outputs, masked_embeddings], axis=1)
# 解码输入。
decoder_outputs = self.decoder(decoder_inputs)
decoder_patches = self.patch_layer(decoder_outputs)
loss_patch = tf.gather(patches, mask_indices, axis=1, batch_dims=1)
loss_output = tf.gather(decoder_patches, mask_indices, axis=1, batch_dims=1)
# 计算总损失。
total_loss = self.compute_loss(y=loss_patch, y_pred=loss_output)
return total_loss, loss_patch, loss_output
def train_step(self, images):
with tf.GradientTape() as tape:
total_loss, loss_patch, loss_output = self.calculate_loss(images)
# 应用梯度。
train_vars = [
self.train_augmentation_model.trainable_variables,
self.patch_layer.trainable_variables,
self.patch_encoder.trainable_variables,
self.encoder.trainable_variables,
self.decoder.trainable_variables,
]
grads = tape.gradient(total_loss, train_vars)
tv_list = []
for grad, var in zip(grads, train_vars):
for g, v in zip(grad, var):
tv_list.append((g, v))
self.optimizer.apply_gradients(tv_list)
# 报告进度。
results = {}
for metric in self.metrics:
metric.update_state(loss_patch, loss_output)
results[metric.name] = metric.result()
return results
def test_step(self, images):
total_loss, loss_patch, loss_output = self.calculate_loss(images, test=True)
# 更新跟踪器。
results = {}
for metric in self.metrics:
metric.update_state(loss_patch, loss_output)
results[metric.name] = metric.result()
return results
模型初始化
train_augmentation_model = get_train_augmentation_model()
test_augmentation_model = get_test_augmentation_model()
patch_layer = Patches()
patch_encoder = PatchEncoder()
encoder = create_encoder()
decoder = create_decoder()
mae_model = MaskedAutoencoder(
train_augmentation_model=train_augmentation_model,
test_augmentation_model=test_augmentation_model,
patch_layer=patch_layer,
patch_encoder=patch_encoder,
encoder=encoder,
decoder=decoder,
)
训练回调
可视化回调
# 取得一批测试输入以测量模型的进度。
test_images = next(iter(test_ds))
class TrainMonitor(keras.callbacks.Callback):
def __init__(self, epoch_interval=None):
self.epoch_interval = epoch_interval
def on_epoch_end(self, epoch, logs=None):
if self.epoch_interval and epoch % self.epoch_interval == 0:
test_augmented_images = self.model.test_augmentation_model(test_images)
test_patches = self.model.patch_layer(test_augmented_images)
(
test_unmasked_embeddings,
test_masked_embeddings,
test_unmasked_positions,
test_mask_indices,
test_unmask_indices,
) = self.model.patch_encoder(test_patches)
test_encoder_outputs = self.model.encoder(test_unmasked_embeddings)
test_encoder_outputs = test_encoder_outputs + test_unmasked_positions
test_decoder_inputs = tf.concat(
[test_encoder_outputs, test_masked_embeddings], axis=1
)
test_decoder_outputs = self.model.decoder(test_decoder_inputs)
# 显示一个被遮罩的补丁图像。
test_masked_patch, idx = self.model.patch_encoder.generate_masked_image(
test_patches, test_unmask_indices
)
print(f"\nIdx chosen: {idx}")
original_image = test_augmented_images[idx]
masked_image = self.model.patch_layer.reconstruct_from_patch(
test_masked_patch
)
reconstructed_image = test_decoder_outputs[idx]
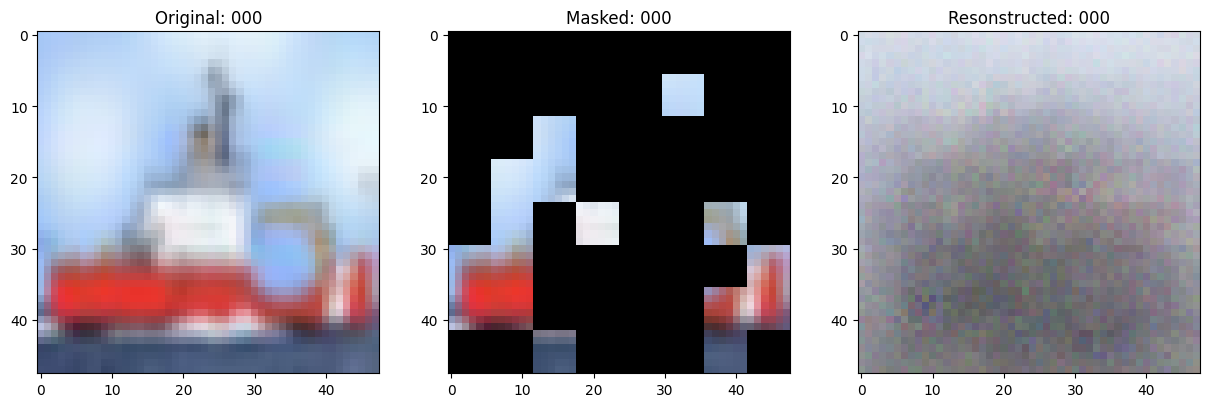
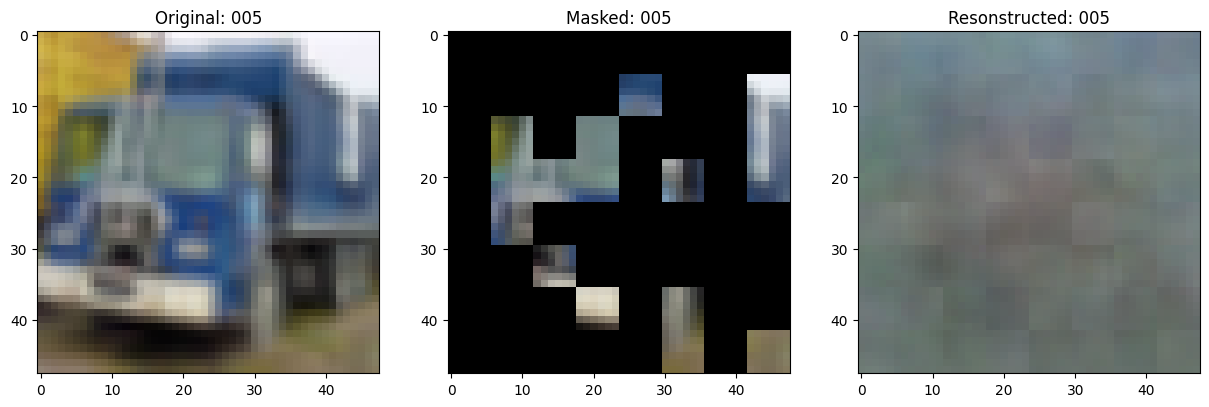
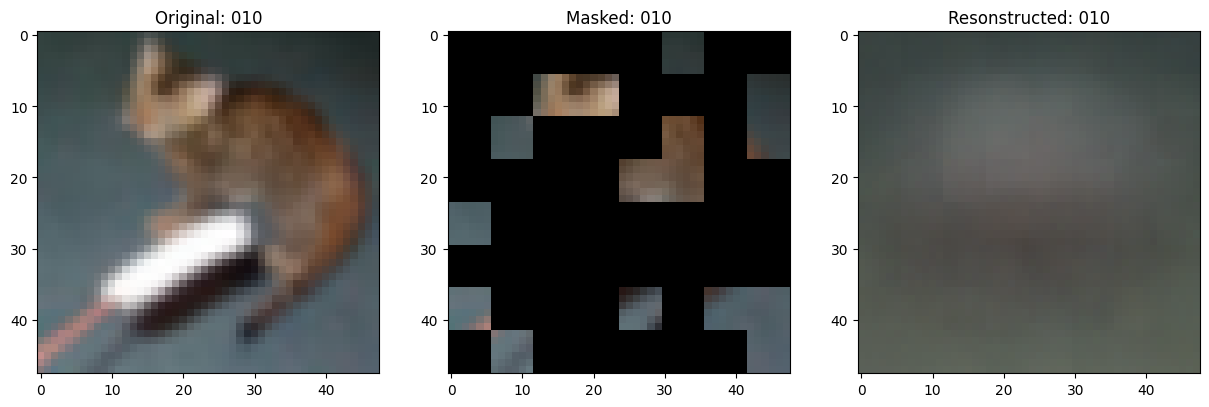
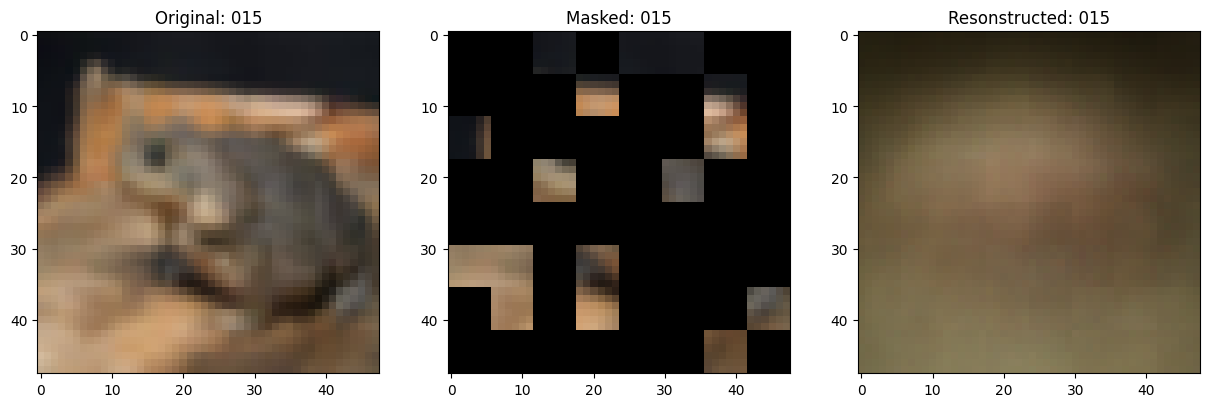
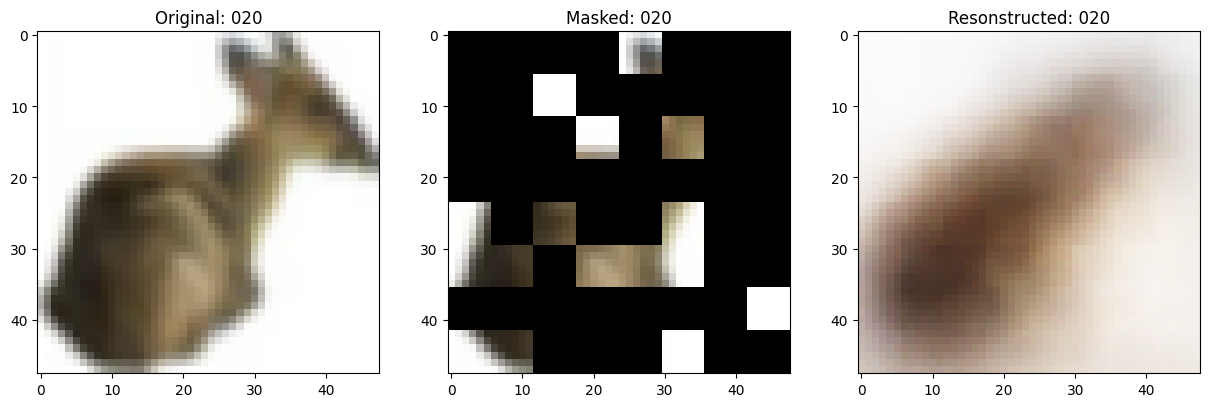
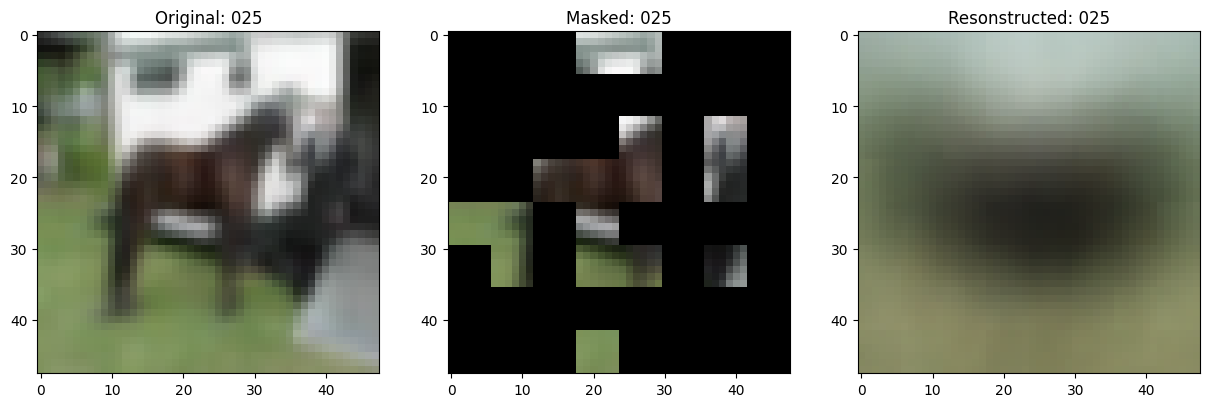
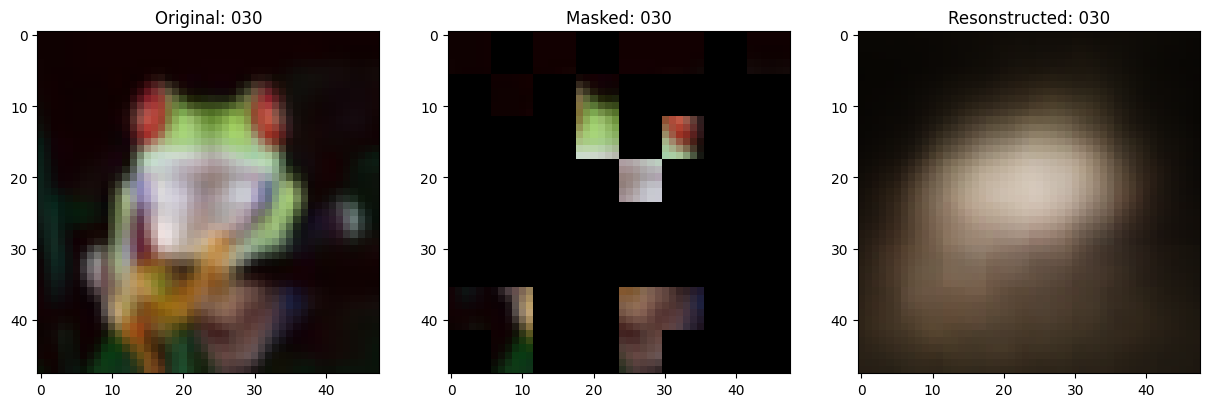
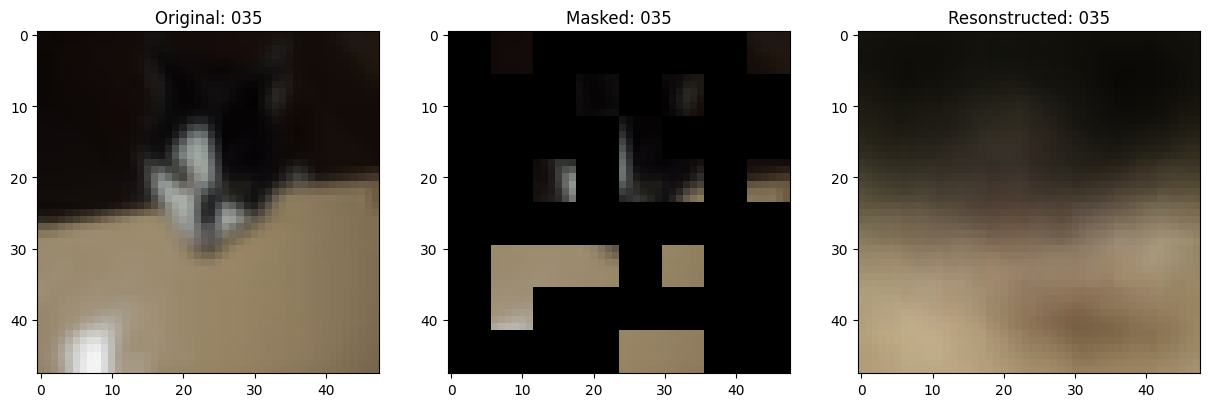
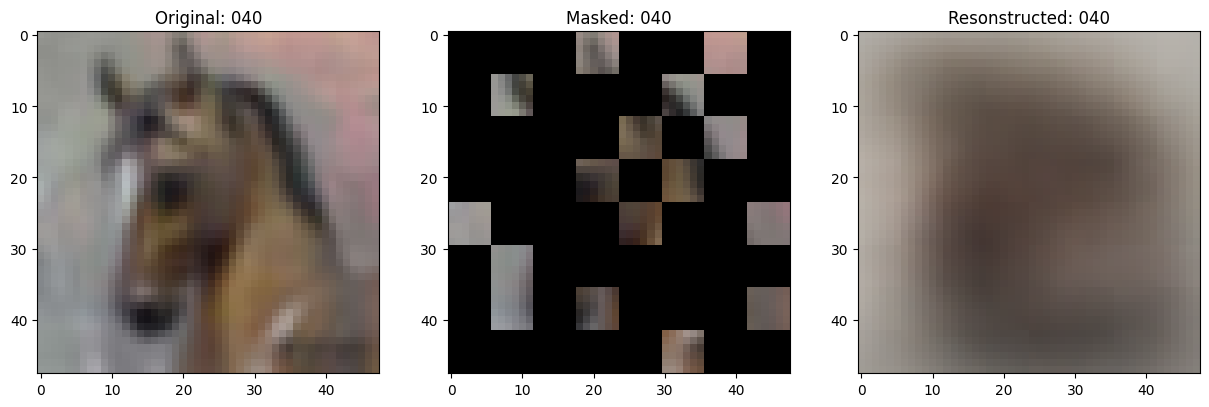
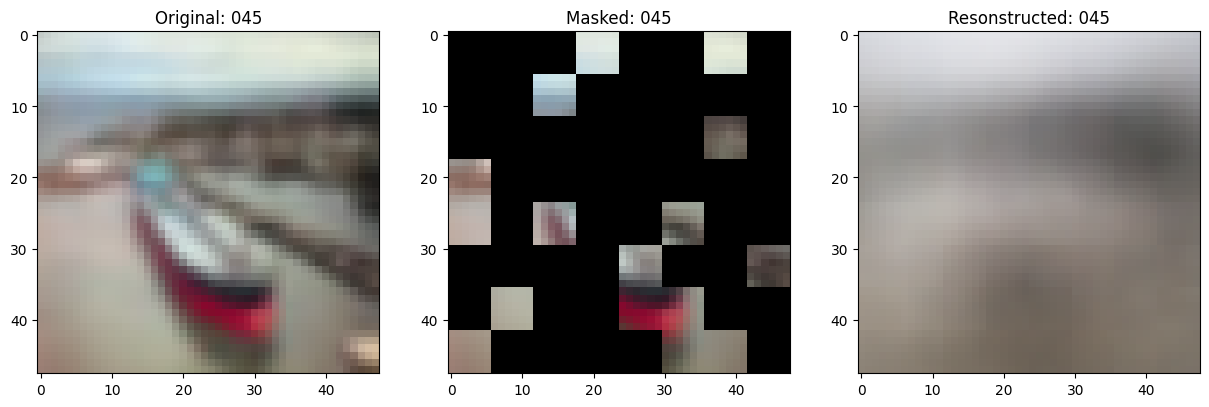
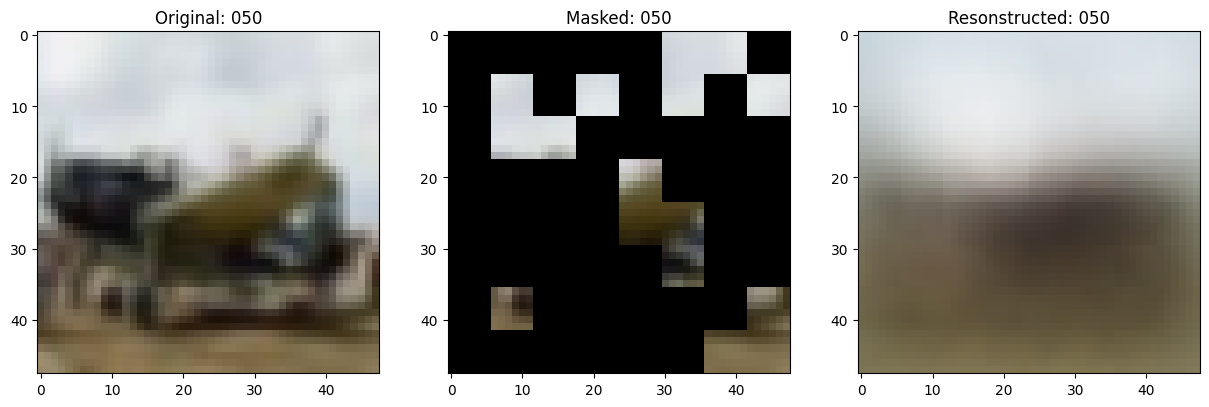
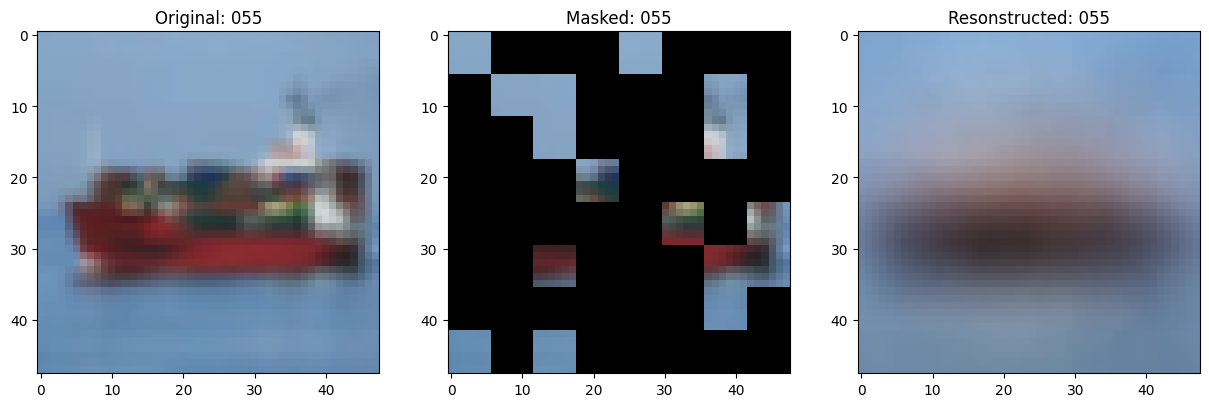
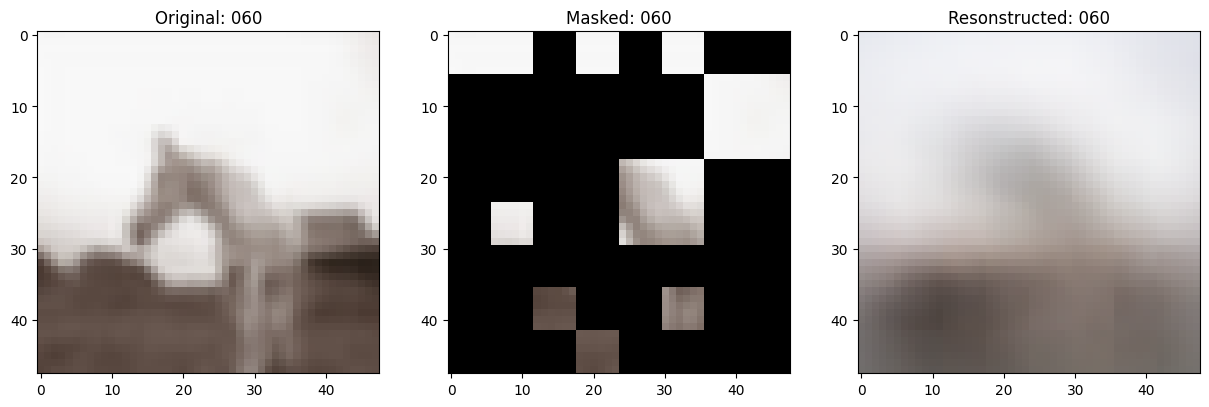
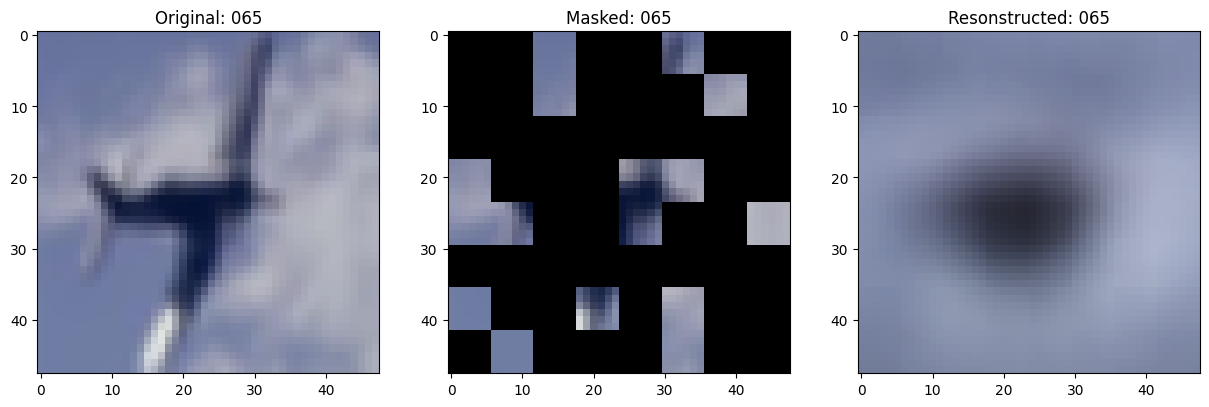
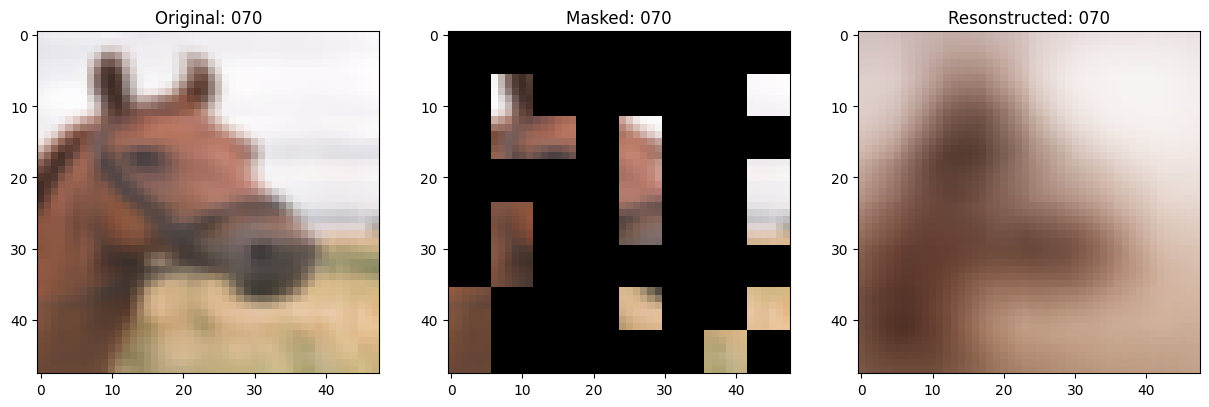
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
ax[0].imshow(original_image)
ax[0].set_title(f"Original: {epoch:03d}")
ax[1].imshow(masked_image)
ax[1].set_title(f"Masked: {epoch:03d}")
ax[2].imshow(reconstructed_image)
ax[2].set_title(f"Resonstructed: {epoch:03d}")
plt.show()
plt.close()
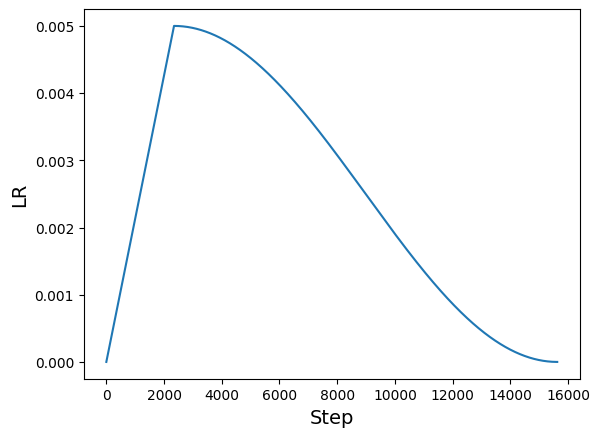
学习率调度
# 部分代码取自:
# https://www.kaggle.com/ashusma/training-rfcx-tensorflow-tpu-effnet-b2.
class WarmUpCosine(keras.optimizers.schedules.LearningRateSchedule):
def __init__(
self, learning_rate_base, total_steps, warmup_learning_rate, warmup_steps
):
super().__init__()
self.learning_rate_base = learning_rate_base
self.total_steps = total_steps
self.warmup_learning_rate = warmup_learning_rate
self.warmup_steps = warmup_steps
self.pi = tf.constant(np.pi)
def __call__(self, step):
if self.total_steps < self.warmup_steps:
raise ValueError("Total_steps must be larger or equal to warmup_steps.")
cos_annealed_lr = tf.cos(
self.pi
* (tf.cast(step, tf.float32) - self.warmup_steps)
/ float(self.total_steps - self.warmup_steps)
)
learning_rate = 0.5 * self.learning_rate_base * (1 + cos_annealed_lr)
if self.warmup_steps > 0:
if self.learning_rate_base < self.warmup_learning_rate:
raise ValueError(
"Learning_rate_base must be larger or equal to "
"warmup_learning_rate."
)
slope = (
self.learning_rate_base - self.warmup_learning_rate
) / self.warmup_steps
warmup_rate = slope * tf.cast(step, tf.float32) + self.warmup_learning_rate
learning_rate = tf.where(
step < self.warmup_steps, warmup_rate, learning_rate
)
return tf.where(
step > self.total_steps, 0.0, learning_rate, name="learning_rate"
)
total_steps = int((len(x_train) / BATCH_SIZE) * EPOCHS)
warmup_epoch_percentage = 0.15
warmup_steps = int(total_steps * warmup_epoch_percentage)
scheduled_lrs = WarmUpCosine(
learning_rate_base=LEARNING_RATE,
total_steps=total_steps,
warmup_learning_rate=0.0,
warmup_steps=warmup_steps,
)
lrs = [scheduled_lrs(step) for step in range(total_steps)]
plt.plot(lrs)
plt.xlabel("Step", fontsize=14)
plt.ylabel("LR", fontsize=14)
plt.show()
# 整合回调。
train_callbacks = [TrainMonitor(epoch_interval=5)]
模型编译和训练
optimizer = keras.optimizers.AdamW(
learning_rate=scheduled_lrs, weight_decay=WEIGHT_DECAY
)
# 编译并预训练模型。
mae_model.compile(
optimizer=optimizer, loss=keras.losses.MeanSquaredError(), metrics=["mae"]
)
history = mae_model.fit(
train_ds,
epochs=EPOCHS,
validation_data=val_ds,
callbacks=train_callbacks,
)
# 测量模型性能。
loss, mae = mae_model.evaluate(test_ds)
print(f"Loss: {loss:.2f}")
print(f"MAE: {mae:.2f}")
Epoch 1/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 80ms/step - mae: 0.2035 - loss: 0.4828
Idx chosen: 92
157/157 ━━━━━━━━━━━━━━━━━━━━ 47s 95ms/step - mae: 0.2033 - loss: 0.4828 - val_loss: 0.5225 - val_mae: 0.1600
Epoch 2/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1592 - loss: 0.5128 - val_loss: 0.5290 - val_mae: 0.1511
Epoch 3/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1530 - loss: 0.5193 - val_loss: 0.5336 - val_mae: 0.1478
Epoch 4/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1502 - loss: 0.5220 - val_loss: 0.5298 - val_mae: 0.1436
Epoch 5/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1458 - loss: 0.5245 - val_loss: 0.5296 - val_mae: 0.1405
Epoch 6/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 81ms/step - mae: 0.1414 - loss: 0.5265
Idx chosen: 14
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 88ms/step - mae: 0.1414 - loss: 0.5265 - val_loss: 0.5328 - val_mae: 0.1402
Epoch 7/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1399 - loss: 0.5278 - val_loss: 0.5361 - val_mae: 0.1360
Epoch 8/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1389 - loss: 0.5285 - val_loss: 0.5365 - val_mae: 0.1424
Epoch 9/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1379 - loss: 0.5295 - val_loss: 0.5312 - val_mae: 0.1345
Epoch 10/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1352 - loss: 0.5308 - val_loss: 0.5374 - val_mae: 0.1321
Epoch 11/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 81ms/step - mae: 0.1339 - loss: 0.5317
Idx chosen: 106
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 87ms/step - mae: 0.1339 - loss: 0.5317 - val_loss: 0.5392 - val_mae: 0.1330
Epoch 12/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1321 - loss: 0.5331 - val_loss: 0.5383 - val_mae: 0.1301
Epoch 13/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1317 - loss: 0.5343 - val_loss: 0.5405 - val_mae: 0.1322
Epoch 14/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1326 - loss: 0.5338 - val_loss: 0.5404 - val_mae: 0.1280
Epoch 15/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 84ms/step - mae: 0.1297 - loss: 0.5343 - val_loss: 0.5444 - val_mae: 0.1261
Epoch 16/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 82ms/step - mae: 0.1276 - loss: 0.5361
Idx chosen: 71
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 91ms/step - mae: 0.1276 - loss: 0.5362 - val_loss: 0.5456 - val_mae: 0.1243
Epoch 17/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1262 - loss: 0.5382 - val_loss: 0.5427 - val_mae: 0.1233
Epoch 18/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1221 - loss: 0.5407 - val_loss: 0.5473 - val_mae: 0.1196
Epoch 19/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1209 - loss: 0.5412 - val_loss: 0.5511 - val_mae: 0.1176
Epoch 20/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1202 - loss: 0.5422 - val_loss: 0.5515 - val_mae: 0.1167
Epoch 21/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1186 - loss: 0.5430
Idx chosen: 188
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 85ms/step - mae: 0.1186 - loss: 0.5430 - val_loss: 0.5546 - val_mae: 0.1168
Epoch 22/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1171 - loss: 0.5446 - val_loss: 0.5500 - val_mae: 0.1155
Epoch 23/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1161 - loss: 0.5457 - val_loss: 0.5559 - val_mae: 0.1135
Epoch 24/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1135 - loss: 0.5479 - val_loss: 0.5521 - val_mae: 0.1112
Epoch 25/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1128 - loss: 0.5480 - val_loss: 0.5505 - val_mae: 0.1122
Epoch 26/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1123 - loss: 0.5470
Idx chosen: 20
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1123 - loss: 0.5470 - val_loss: 0.5572 - val_mae: 0.1127
第27/100轮
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1114 - loss: 0.5487 - val_loss: 0.5555 - val_mae: 0.1092
第28/100轮
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1108 - loss: 0.5492 - val_loss: 0.5569 - val_mae: 0.1110
第29/100轮
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1104 - loss: 0.5491 - val_loss: 0.5517 - val_mae: 0.1110
第30/100轮
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1099 - loss: 0.5490 - val_loss: 0.5543 - val_mae: 0.1104
第31/100轮
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1095 - loss: 0.5501
选择的索引: 102
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1095 - loss: 0.5501 - val_loss: 0.5578 - val_mae: 0.1108
Epoch 32/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1089 - loss: 0.5503 - val_loss: 0.5620 - val_mae: 0.1081
Epoch 33/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1079 - loss: 0.5509 - val_loss: 0.5618 - val_mae: 0.1067
Epoch 34/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1067 - loss: 0.5524 - val_loss: 0.5627 - val_mae: 0.1059
Epoch 35/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1068 - loss: 0.5515 - val_loss: 0.5576 - val_mae: 0.1050
Epoch 36/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1057 - loss: 0.5526
Idx chosen: 121
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1057 - loss: 0.5526 - val_loss: 0.5627 - val_mae: 0.1050
Epoch 37/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1065 - loss: 0.5534 - val_loss: 0.5638 - val_mae: 0.1050
Epoch 38/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1055 - loss: 0.5528 - val_loss: 0.5527 - val_mae: 0.1083
Epoch 39/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 20s 82ms/step - mae: 0.1056 - loss: 0.5516 - val_loss: 0.5562 - val_mae: 0.1044
Epoch 40/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1053 - loss: 0.5528 - val_loss: 0.5567 - val_mae: 0.1051
Epoch 41/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - mae: 0.1049 - loss: 0.5533
Idx chosen: 210
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 85ms/step - mae: 0.1049 - loss: 0.5533 - val_loss: 0.5620 - val_mae: 0.1030
Epoch 42/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1041 - loss: 0.5534 - val_loss: 0.5650 - val_mae: 0.1052
Epoch 43/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1048 - loss: 0.5526 - val_loss: 0.5619 - val_mae: 0.1027
Epoch 44/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1037 - loss: 0.5543 - val_loss: 0.5615 - val_mae: 0.1031
Epoch 45/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1036 - loss: 0.5535 - val_loss: 0.5575 - val_mae: 0.1026
Epoch 46/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - mae: 0.1032 - loss: 0.5537
Idx chosen: 214
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 85ms/step - mae: 0.1032 - loss: 0.5537 - val_loss: 0.5549 - val_mae: 0.1037
Epoch 47/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 84ms/step - mae: 0.1035 - loss: 0.5539 - val_loss: 0.5597 - val_mae: 0.1031
Epoch 48/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1033 - loss: 0.5533 - val_loss: 0.5650 - val_mae: 0.1013
Epoch 49/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1027 - loss: 0.5543 - val_loss: 0.5571 - val_mae: 0.1028
Epoch 50/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1024 - loss: 0.5548 - val_loss: 0.5592 - val_mae: 0.1018
Epoch 51/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - mae: 0.1025 - loss: 0.5543
Idx chosen: 74
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 85ms/step - mae: 0.1025 - loss: 0.5543 - val_loss: 0.5645 - val_mae: 0.1007
Epoch 52/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1025 - loss: 0.5544 - val_loss: 0.5616 - val_mae: 0.1004
Epoch 53/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1014 - loss: 0.5547 - val_loss: 0.5594 - val_mae: 0.1007
Epoch 54/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1014 - loss: 0.5550 - val_loss: 0.5687 - val_mae: 0.1012
Epoch 55/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1022 - loss: 0.5551 - val_loss: 0.5572 - val_mae: 0.1018
Epoch 56/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1015 - loss: 0.5558
Idx chosen: 202
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1015 - loss: 0.5558 - val_loss: 0.5619 - val_mae: 0.0996
Epoch 57/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1008 - loss: 0.5550 - val_loss: 0.5614 - val_mae: 0.0996
Epoch 58/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1004 - loss: 0.5557 - val_loss: 0.5620 - val_mae: 0.0995
Epoch 59/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1002 - loss: 0.5558 - val_loss: 0.5612 - val_mae: 0.0997
Epoch 60/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.1005 - loss: 0.5563 - val_loss: 0.5598 - val_mae: 0.1000
Epoch 61/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1001 - loss: 0.5564
Idx chosen: 87
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1001 - loss: 0.5564 - val_loss: 0.5606 - val_mae: 0.0998
Epoch 62/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.0998 - loss: 0.5562 - val_loss: 0.5643 - val_mae: 0.0988
Epoch 63/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.1001 - loss: 0.5556 - val_loss: 0.5657 - val_mae: 0.0985
Epoch 64/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0998 - loss: 0.5566 - val_loss: 0.5624 - val_mae: 0.0989
Epoch 65/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0994 - loss: 0.5564 - val_loss: 0.5576 - val_mae: 0.0999
Epoch 66/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.0993 - loss: 0.5567
Idx chosen: 116
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.0993 - loss: 0.5567 - val_loss: 0.5572 - val_mae: 0.1000
Epoch 67/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0990 - loss: 0.5570 - val_loss: 0.5619 - val_mae: 0.0981
Epoch 68/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0987 - loss: 0.5578 - val_loss: 0.5644 - val_mae: 0.0973
Epoch 69/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0981 - loss: 0.5577 - val_loss: 0.5639 - val_mae: 0.0976
Epoch 70/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0986 - loss: 0.5563 - val_loss: 0.5601 - val_mae: 0.0989
Epoch 71/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0982 - loss: 0.5578
Idx chosen: 99
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 84ms/step - mae: 0.0982 - loss: 0.5577 - val_loss: 0.5628 - val_mae: 0.0970
Epoch 72/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0979 - loss: 0.5569 - val_loss: 0.5637 - val_mae: 0.0968
Epoch 73/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0979 - loss: 0.5575 - val_loss: 0.5606 - val_mae: 0.0975
Epoch 74/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0977 - loss: 0.5572 - val_loss: 0.5628 - val_mae: 0.0967
Epoch 75/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0975 - loss: 0.5572 - val_loss: 0.5631 - val_mae: 0.0964
Epoch 76/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0973 - loss: 0.5580
Idx chosen: 103
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.0973 - loss: 0.5579 - val_loss: 0.5628 - val_mae: 0.0967
Epoch 77/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0974 - loss: 0.5579 - val_loss: 0.5638 - val_mae: 0.0963
Epoch 78/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0968 - loss: 0.5585 - val_loss: 0.5615 - val_mae: 0.0967
Epoch 79/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0969 - loss: 0.5578 - val_loss: 0.5641 - val_mae: 0.0959
Epoch 80/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0967 - loss: 0.5584 - val_loss: 0.5619 - val_mae: 0.0962
Epoch 81/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0965 - loss: 0.5578
Idx chosen: 151
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.0965 - loss: 0.5578 - val_loss: 0.5651 - val_mae: 0.0957
Epoch 82/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0965 - loss: 0.5583 - val_loss: 0.5644 - val_mae: 0.0957
Epoch 83/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0962 - loss: 0.5584 - val_loss: 0.5649 - val_mae: 0.0954
Epoch 84/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0962 - loss: 0.5586 - val_loss: 0.5611 - val_mae: 0.0962
Epoch 85/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0961 - loss: 0.5582 - val_loss: 0.5638 - val_mae: 0.0956
Epoch 86/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0961 - loss: 0.5584
Idx chosen: 130
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.0961 - loss: 0.5584 - val_loss: 0.5641 - val_mae: 0.0954
Epoch 87/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0959 - loss: 0.5580 - val_loss: 0.5641 - val_mae: 0.0953
Epoch 88/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0960 - loss: 0.5583 - val_loss: 0.5642 - val_mae: 0.0953
Epoch 89/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0958 - loss: 0.5591 - val_loss: 0.5635 - val_mae: 0.0953
Epoch 90/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0957 - loss: 0.5587 - val_loss: 0.5648 - val_mae: 0.0948
Epoch 91/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0957 - loss: 0.5585
Idx chosen: 149
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 84ms/step - mae: 0.0957 - loss: 0.5585 - val_loss: 0.5636 - val_mae: 0.0952
Epoch 92/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0957 - loss: 0.5593 - val_loss: 0.5642 - val_mae: 0.0950
Epoch 93/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0957 - loss: 0.5598 - val_loss: 0.5635 - val_mae: 0.0950
Epoch 94/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0956 - loss: 0.5587 - val_loss: 0.5641 - val_mae: 0.0950
Epoch 95/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0955 - loss: 0.5587 - val_loss: 0.5637 - val_mae: 0.0950
Epoch 96/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0956 - loss: 0.5585
Idx chosen: 52
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 87ms/step - mae: 0.0956 - loss: 0.5585 - val_loss: 0.5643 - val_mae: 0.0950
Epoch 97/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0956 - loss: 0.5587 - val_loss: 0.5642 - val_mae: 0.0950
Epoch 98/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0954 - loss: 0.5586 - val_loss: 0.5639 - val_mae: 0.0950
Epoch 99/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0954 - loss: 0.5580 - val_loss: 0.5641 - val_mae: 0.0950
Epoch 100/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0955 - loss: 0.5587 - val_loss: 0.5639 - val_mae: 0.0951
40/40 ━━━━━━━━━━━━━━━━━━━━ 1s 13ms/step - mae: 0.0955 - loss: 0.5684
Loss: 0.57
MAE: 0.10
使用线性探测进行评估
提取编码器模型及其他层
# 提取数据增强层。
train_augmentation_model = mae_model.train_augmentation_model
test_augmentation_model = mae_model.test_augmentation_model
# 提取补丁层。
patch_layer = mae_model.patch_layer
patch_encoder = mae_model.patch_encoder
patch_encoder.downstream = True # 将下游标志切换为 True。
# 提取编码器。
encoder = mae_model.encoder
# 打包为模型。
downstream_model = keras.Sequential(
[
layers.Input((IMAGE_SIZE, IMAGE_SIZE, 3)),
patch_layer,
patch_encoder,
encoder,
layers.BatchNormalization(), # 参见 A.1(线性探测)。
layers.GlobalAveragePooling1D(),
layers.Dense(NUM_CLASSES, activation="softmax"),
],
name="linear_probe_model",
)
# 仅 `downstream_model` 的最终分类层应可训练。
for layer in downstream_model.layers[:-1]:
layer.trainable = False
downstream_model.summary()
Model: "linear_probe_model"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩ │ patches_1 (Patches) │ (None, 64, 108) │ 0 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ patch_encoder_1 (PatchEncoder) │ (None, 64, 128) │ 22,144 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ mae_encoder (Functional) │ (None, 64, 128) │ 1,981,696 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ batch_normalization │ (无, 64, 128) │ 512 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ global_average_pooling1d │ (无, 128) │ 0 │ │ (GlobalAveragePooling1D) │ │ │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ dense_20 (Dense) │ (无, 10) │ 1,290 │ └─────────────────────────────────┴───────────────────────────┴────────────┘
总参数量: 2,005,642 (7.65 MB)
可训练参数: 1,290 (5.04 KB)
非可训练参数: 2,004,352 (7.65 MB)
我们正在使用平均池化从MAE编码器中提取学习到的表示。 另一种方法是在预训练期间在编码器内部使用一个可学习的虚拟标记(类似于[CLS]标记)。然后,我们可以在下游任务中从该标记中提取表示。
为线性探测准备数据集
def prepare_data(images, labels, is_train=True):
if is_train:
augmentation_model = train_augmentation_model
else:
augmentation_model = test_augmentation_model
dataset = tf.data.Dataset.from_tensor_slices((images, labels))
if is_train:
dataset = dataset.shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE).map(
lambda x, y: (augmentation_model(x), y), num_parallel_calls=AUTO
)
return dataset.prefetch(AUTO)
train_ds = prepare_data(x_train, y_train)
val_ds = prepare_data(x_train, y_train, is_train=False)
test_ds = prepare_data(x_test, y_test, is_train=False)
执行线性探测
linear_probe_epochs = 50
linear_prob_lr = 0.1
warm_epoch_percentage = 0.1
steps = int((len(x_train) // BATCH_SIZE) * linear_probe_epochs)
warmup_steps = int(steps * warm_epoch_percentage)
scheduled_lrs = WarmUpCosine(
learning_rate_base=linear_prob_lr,
total_steps=steps,
warmup_learning_rate=0.0,
warmup_steps=warmup_steps,
)
optimizer = keras.optimizers.SGD(learning_rate=scheduled_lrs, momentum=0.9)
downstream_model.compile(
optimizer=optimizer, loss="sparse_categorical_crossentropy", metrics=["accuracy"]
)
downstream_model.fit(train_ds, validation_data=val_ds, epochs=linear_probe_epochs)
loss, accuracy = downstream_model.evaluate(test_ds)
accuracy = round(accuracy * 100, 2)
print(f"测试集上的准确率: {accuracy}%.")
Epoch 1/50
7/157 ━━━━━━━━━━━━━━━━━━━━ 3s 21ms/step - 准确率: 0.1183 - 损失: 3.3939
警告: 所有在调用 absl::InitializeLog() 之前的日志消息都写入 STDERR
I0000 00:00:1700264823.481598 64012 device_compiler.h:187] 使用 XLA 编译集群! 此行在进程的生命周期内最多记录一次。
157/157 ━━━━━━━━━━━━━━━━━━━━ 70s 242ms/step - 准确率: 0.1967 - 损失: 2.6073 - 验证准确率: 0.3631 - 验证损失: 1.7846
Epoch 2/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - 准确率: 0.3521 - 损失: 1.8063 - 验证准确率: 0.3677 - 验证损失: 1.7301
Epoch 3/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3580 - 损失: 1.7580 - 验证准确率: 0.3649 - 验证损失: 1.7326
Epoch 4/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3617 - 损失: 1.7471 - 验证准确率: 0.3810 - 验证损失: 1.7353
Epoch 5/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 35ms/step - 准确率: 0.3547 - 损失: 1.7728 - 验证准确率: 0.3526 - 验证损失: 1.8496
Epoch 6/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 35ms/step - 准确率: 0.3546 - 损失: 1.7866 - 验证准确率: 0.3896 - 验证损失: 1.7583
Epoch 7/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 37ms/step - 准确率: 0.3587 - 损失: 1.7924 - 验证准确率: 0.3674 - 验证损失: 1.7729
Epoch 8/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 38ms/step - 准确率: 0.3616 - 损失: 1.7912 - 验证准确率: 0.3685 - 验证损失: 1.7928
Epoch 9/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 36ms/step - 准确率: 0.3707 - 损失: 1.7543 - 验证准确率: 0.3568 - 验证损失: 1.7943
Epoch 10/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3719 - 损失: 1.7451 - 验证准确率: 0.3859 - 验证损失: 1.7230
Epoch 11/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3781 - 损失: 1.7384 - 验证准确率: 0.3711 - 验证损失: 1.7608
Epoch 12/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 35ms/step - 准确率: 0.3791 - 损失: 1.7249 - 验证准确率: 0.4004 - 验证损失: 1.6961
Epoch 13/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3818 - 损失: 1.7303 - 验证准确率: 0.3501 - 验证损失: 1.8506
Epoch 14/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3841 - 损失: 1.7179 - 验证准确率: 0.3810 - 验证损失: 1.8033
Epoch 15/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3818 - 损失: 1.7172 - 验证准确率: 0.4168 - 验证损失: 1.6507
Epoch 16/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 36ms/step - 准确率: 0.3851 - 损失: 1.7059 - 验证准确率: 0.3806 - 验证损失: 1.7581
Epoch 17/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3747 - 损失: 1.7356 - 验证准确率: 0.4094 - 验证损失: 1.6466
Epoch 18/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - 准确率: 0.3828 - 损失: 1.7221 - 验证准确率: 0.4015 - 验证损失: 1.6757
Epoch 19/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3889 - 损失: 1.6939 - 验证准确率: 0.4102 - 验证损失: 1.6392
Epoch 20/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3943 - 损失: 1.6857 - 验证准确率: 0.4028 - 验证损失: 1.6518
Epoch 21/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3870 - 损失: 1.6970 - 验证准确率: 0.3949 - 验证损失: 1.7283
Epoch 22/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3893 - 损失: 1.6838 - 验证准确率: 0.4207 - 验证损失: 1.6292
Epoch 23/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - 准确率: 0.4005 - 损失: 1.6606 - 验证准确率: 0.4152 - 验证损失: 1.6320
Epoch 24/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3978 - 损失: 1.6556 - 验证准确率: 0.4042 - 验证损失: 1.6657
Epoch 25/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4029 - 损失: 1.6464 - 验证准确率: 0.4198 - 验证损失: 1.6033
Epoch 26/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.3974 - 损失: 1.6638 - 验证准确率: 0.4278 - 验证损失: 1.5731
Epoch 27/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 37ms/step - 准确率: 0.4035 - 损失: 1.6370 - 验证准确率: 0.4302 - 验证损失: 1.5663
Epoch 28/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4027 - 损失: 1.6349 - 验证准确率: 0.4458 - 验证损失: 1.5349
Epoch 29/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4054 - 损失: 1.6196 - 验证准确率: 0.4349 - 验证损失: 1.5709
Epoch 30/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - 准确率: 0.4070 - 损失: 1.6061 - 验证准确率: 0.4297 - 验证损失: 1.5578
Epoch 31/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4105 - 损失: 1.6172 - 验证准确率: 0.4250 - 验证损失: 1.5735
Epoch 32/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4197 - 损失: 1.5960 - 验证准确率: 0.4259 - 验证损失: 1.5677
Epoch 33/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4156 - 损失: 1.5989 - 验证准确率: 0.4400 - 验证损失: 1.5395
Epoch 34/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - 准确率: 0.4214 - 损失: 1.5862 - 验证准确率: 0.4486 - 验证损失: 1.5237
Epoch 35/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4208 - 损失: 1.5763 - 验证准确率: 0.4188 - 验证损失: 1.5925
Epoch 36/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4227 - 损失: 1.5803 - 验证准确率: 0.4525 - 验证损失: 1.5174
Epoch 37/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4267 - 损失: 1.5700 - 验证准确率: 0.4463 - 验证损失: 1.5330
Epoch 38/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 37ms/step - 准确率: 0.4283 - 损失: 1.5649 - 验证准确率: 0.4348 - 验证损失: 1.5482
Epoch 39/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4332 - 损失: 1.5581 - 验证准确率: 0.4486 - 验证损失: 1.5251
Epoch 40/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4290 - 损失: 1.5596 - 验证准确率: 0.4489 - 验证损失: 1.5221
Epoch 41/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4318 - 损失: 1.5589 - 验证准确率: 0.4494 - 验证损失: 1.5202
Epoch 42/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4317 - 损失: 1.5514 - 验证准确率: 0.4505 - 验证损失: 1.5184
Epoch 43/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4353 - 损失: 1.5504 - 验证准确率: 0.4561 - 验证损失: 1.5081
Epoch 44/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4369 - 损失: 1.5510 - 验证准确率: 0.4581 - 验证损失: 1.5092
Epoch 45/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 35ms/step - 准确率: 0.4379 - 损失: 1.5428 - 验证准确率: 0.4555 - 验证损失: 1.5099
Epoch 46/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4421 - 损失: 1.5475 - 验证准确率: 0.4579 - 验证损失: 1.5073
Epoch 47/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4434 - 损失: 1.5390 - 验证准确率: 0.4593 - 验证损失: 1.5052
Epoch 48/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - 准确率: 0.4418 - 损失: 1.5373 - 验证准确率: 0.4600 - 验证损失: 1.5038
Epoch 49/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 38ms/step - 准确率: 0.4400 - 损失: 1.5367 - 验证准确率: 0.4596 - 验证损失: 1.5045
Epoch 50/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - 准确率: 0.4448 - 损失: 1.5321 - 验证准确率: 0.4595 - 验证损失: 1.5048
40/40 ━━━━━━━━━━━━━━━━━━━━ 3s 71ms/step - 准确率: 0.4496 - 损失: 1.5088
测试集上的准确率: 44.66%。
我们相信,通过更复杂的超参数调整过程和更长的预训练,进一步提高这一性能是可能的。为了进行比较,我们使用编码器架构 从零开始训练 以完全监督的方式进行训练。这使我们得到了约76%的测试 top-1 精度。MAE的作者在ImageNet-1k数据集及 其他下游任务(如目标检测和语义分割)上展示了强大的性能。
最后说明
我们将感兴趣的读者引向keras.io上关于自监督学习的其他示例:
在计算机视觉中使用BERT风格的预训练的想法也在 Selfie中有所探索,但未能展示强大的结果。 另一个探索掩码图像建模思想的并行工作是 SimMIM。最后,作为一个有趣的事实,我们,作为 这个示例的作者,在2020年也探索了“重建作为预文本任务” 的想法,但我们未能防止网络表示崩溃,因此我们未能获得强大的下游性能。
我们要感谢Xinlei Chen (MAE的作者之一)为我们提供的有益讨论。我们对 JarvisLabs和 Google Developers Experts 计划提供GPU信用表示感谢。
