图像相似性搜索的度量学习
作者: Mat Kelcey
创建日期: 2020/06/05
最后修改: 2020/06/09
描述: 在CIFAR-10图像上使用相似性度量学习的示例。
概述
度量学习旨在训练模型,将输入嵌入到高维空间中,使得根据训练方案定义的“相似”输入彼此接近。经过训练后,这些模型可以为下游系统生成嵌入,那里这种相似性是有用的;示例包括作为搜索的排名信号或作为另一个监督问题的预训练嵌入模型。
有关度量学习的更详细概述,请参见:
设置
将Keras后端设置为tensorflow。
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import random
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from collections import defaultdict
from PIL import Image
from sklearn.metrics import ConfusionMatrixDisplay
import keras
from keras import layers
数据集
在本示例中,我们将使用 CIFAR-10 数据集。
from keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train.astype("float32") / 255.0
y_train = np.squeeze(y_train)
x_test = x_test.astype("float32") / 255.0
y_test = np.squeeze(y_test)
为了了解数据集,我们可以可视化25个随机示例的网格。
height_width = 32
def show_collage(examples):
box_size = height_width + 2
num_rows, num_cols = examples.shape[:2]
collage = Image.new(
mode="RGB",
size=(num_cols * box_size, num_rows * box_size),
color=(250, 250, 250),
)
for row_idx in range(num_rows):
for col_idx in range(num_cols):
array = (np.array(examples[row_idx, col_idx]) * 255).astype(np.uint8)
collage.paste(
Image.fromarray(array), (col_idx * box_size, row_idx * box_size)
)
# 进行可视化时尺寸加倍。
collage = collage.resize((2 * num_cols * box_size, 2 * num_rows * box_size))
return collage
# 显示5x5的随机图像拼贴。
sample_idxs = np.random.randint(0, 50000, size=(5, 5))
examples = x_train[sample_idxs]
show_collage(examples)

度量学习并不是将训练数据作为显式的 (X, y) 对提供,而是使用在我们想要表达相似性时相关的多个实例。在我们的示例中,我们将使用同一类别的实例来表示相似性;单个训练实例将不是一幅图像,而是一对同类图像。当提到这一对图像时,我们将使用常见的度量学习名称“锚点”(anchor)(随机选择的一幅图像)和“正样本”(positive)(同一类别的另一幅随机选择的图像)。
为了实现这一点,我们需要构建一种查找方式,将类别映射到该类别的实例。在生成训练数据时,我们将从此查找中进行采样。
class_idx_to_train_idxs = defaultdict(list)
for y_train_idx, y in enumerate(y_train):
class_idx_to_train_idxs[y].append(y_train_idx)
class_idx_to_test_idxs = defaultdict(list)
for y_test_idx, y in enumerate(y_test):
class_idx_to_test_idxs[y].append(y_test_idx)
在本示例中,我们使用最简单的训练方法;一个批次将由跨类别的 (anchor, positive) 对组成。学习的目标是将锚点和正样本对彼此靠近,并将其与批次中的其他实例拉开。在这种情况下,批次大小将由类别的数量决定;对于CIFAR-10,这是10。
num_classes = 10
class AnchorPositivePairs(keras.utils.Sequence):
def __init__(self, num_batches):
super().__init__()
self.num_batches = num_batches
def __len__(self):
return self.num_batches
def __getitem__(self, _idx):
x = np.empty((2, num_classes, height_width, height_width, 3), dtype=np.float32)
for class_idx in range(num_classes):
examples_for_class = class_idx_to_train_idxs[class_idx]
anchor_idx = random.choice(examples_for_class)
positive_idx = random.choice(examples_for_class)
while positive_idx == anchor_idx:
positive_idx = random.choice(examples_for_class)
x[0, class_idx] = x_train[anchor_idx]
x[1, class_idx] = x_train[positive_idx]
return x
我们可以在另一个拼贴中可视化一个批次。第一行显示了从10个类别中随机选择的锚点,第二行显示了相应的10个正样本。
examples = next(iter(AnchorPositivePairs(num_batches=1)))
show_collage(examples)

嵌入模型
我们定义一个自定义模型,其 train_step 首先嵌入锚点和正样本,然后使用它们的成对点积作为 softmax 的 logits。
class EmbeddingModel(keras.Model):
def train_step(self, data):
# 注意:针对开放问题的权宜之计,稍后删除。
if isinstance(data, tuple):
data = data[0]
anchors, positives = data[0], data[1]
with tf.GradientTape() as tape:
# 运行锚点和正样本模型。
anchor_embeddings = self(anchors, training=True)
positive_embeddings = self(positives, training=True)
# 计算锚点和正样本之间的余弦相似度。由于它们已被归一化,
# 这只是成对的点积。
similarities = keras.ops.einsum(
"ae,pe->ap", anchor_embeddings, positive_embeddings
)
# 由于我们打算将这些用作 logits,因此通过温度进行缩放。
# 这个值通常会作为超参数选择。
temperature = 0.2
similarities /= temperature
# 我们将这些相似度作为 softmax 的 logits。此调用的标签只是
# 序列 [0, 1, 2, ..., num_classes],因为我们希望主对角线上的值
# 对应于锚点/正样本对,具有较高值。此损失将使锚点/正样本对的
# 嵌入靠得更近,而将所有其他对分开。
sparse_labels = keras.ops.arange(num_classes)
loss = self.compute_loss(y=sparse_labels, y_pred=similarities)
# 计算梯度并通过优化器应用。
gradients = tape.gradient(loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(gradients, self.trainable_variables))
# 更新并返回指标(特别是损失值的指标)。
for metric in self.metrics:
# 调用 `self.compile` 会默认添加 [`keras.metrics.Mean`](/api/metrics/metrics_wrappers#mean-class) 损失
if metric.name == "loss":
metric.update_state(loss)
else:
metric.update_state(sparse_labels, similarities)
return {m.name: m.result() for m in self.metrics}
接下来,我们描述将图像映射到嵌入的架构。该模型简单地由一系列 2D 卷积和全局池化组成,并以最终的线性投影到嵌入空间。正如在度量学习中常见的那样,我们对嵌入进行归一化,以便可以使用简单的点积来衡量相似性。为了简化起见,该模型故意较小。
inputs = layers.Input(shape=(height_width, height_width, 3))
x = layers.Conv2D(filters=32, kernel_size=3, strides=2, activation="relu")(inputs)
x = layers.Conv2D(filters=64, kernel_size=3, strides=2, activation="relu")(x)
x = layers.Conv2D(filters=128, kernel_size=3, strides=2, activation="relu")(x)
x = layers.GlobalAveragePooling2D()(x)
embeddings = layers.Dense(units=8, activation=None)(x)
embeddings = layers.UnitNormalization()(embeddings)
model = EmbeddingModel(inputs, embeddings)
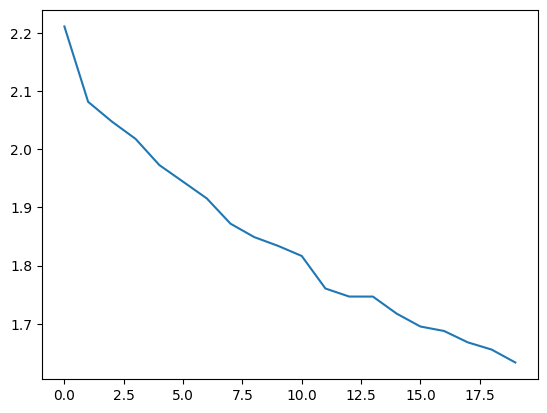
最后我们进行训练。在一个 Google Colab GPU 实例上,这大约需要一分钟。
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
)
history = model.fit(AnchorPositivePairs(num_batches=1000), epochs=20)
plt.plot(history.history["loss"])
plt.show()
第 1 个周期/共 20 个周期
77/1000 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/步 - 损失: 2.2962
警告: 在调用 absl::InitializeLog() 之前的所有日志消息都写入 STDERR
I0000 00:00:1700589927.295343 3724442 device_compiler.h:187] 使用 XLA 编译的集群! 这一行在进程的生命周期内最多记录一次。
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 6s 2ms/步 - 损失: 2.2504
第 2 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 2.1068
第 3 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 2.0646
第 4 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 2.0210
第 5 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.9857
第 6 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.9543
第 7 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.9175
第 8 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.8740
第 9 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.8474
第 10 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.8380
第 11 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.8146
第 12 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.7658
第 13 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.7512
第 14 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.7671
第 15 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.7245
第 16 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.7001
第 17 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.7099
第 18 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.6775
第 19 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.6547
第 20 个周期/共 20 个周期
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/步 - 损失: 1.6356
测试
我们可以通过将模型应用于测试集并考虑嵌入空间中的近邻来审查该模型的质量。
首先,我们嵌入测试集并计算所有近邻。请记住,由于嵌入是单位长度,我们可以通过点乘计算余弦相似度。
near_neighbours_per_example = 10
embeddings = model.predict(x_test)
gram_matrix = np.einsum("ae,be->ab", embeddings, embeddings)
near_neighbours = np.argsort(gram_matrix.T)[:, -(near_neighbours_per_example + 1) :]
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 3ms/step
作为这些嵌入的视觉检查,我们可以为5个随机示例构建近邻的拼贴。下面图像的第一列是随机选择的图像,接下来的10列显示按相似度排序的最近邻居。
num_collage_examples = 5
examples = np.empty(
(
num_collage_examples,
near_neighbours_per_example + 1,
height_width,
height_width,
3,
),
dtype=np.float32,
)
for row_idx in range(num_collage_examples):
examples[row_idx, 0] = x_test[row_idx]
anchor_near_neighbours = reversed(near_neighbours[row_idx][:-1])
for col_idx, nn_idx in enumerate(anchor_near_neighbours):
examples[row_idx, col_idx + 1] = x_test[nn_idx]
show_collage(examples)

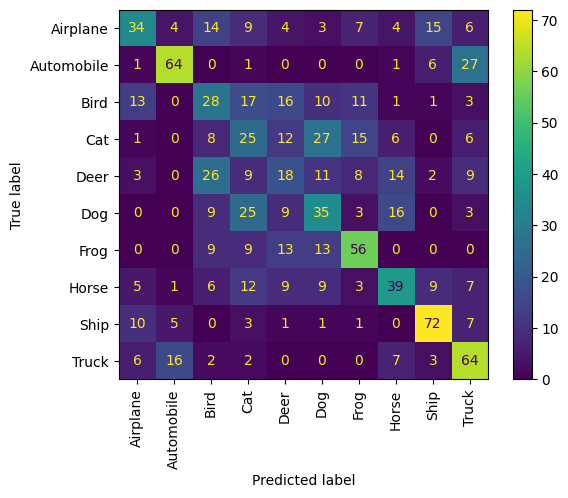
我们还可以通过考虑近邻的正确性以混淆矩阵的形式获得性能的量化视图。
让我们从每个类别中抽样10个示例,并将它们的近邻视为预测形式;也就是说,示例及其近邻是否共享相同类别?
我们观察到每个动物类通常表现良好,且与其他动物类的混淆最多。车辆类遵循相同的模式。
confusion_matrix = np.zeros((num_classes, num_classes))
# 对于每个类别。
for class_idx in range(num_classes):
# 考虑10个示例。
example_idxs = class_idx_to_test_idxs[class_idx][:10]
for y_test_idx in example_idxs:
# 并计算其近邻的类别。
for nn_idx in near_neighbours[y_test_idx][:-1]:
nn_class_idx = y_test[nn_idx]
confusion_matrix[class_idx, nn_class_idx] += 1
# 显示混淆矩阵。
labels = [
"飞机",
"汽车",
"鸟",
"猫",
"鹿",
"狗",
"青蛙",
"马",
"船",
"卡车",
]
disp = ConfusionMatrixDisplay(confusion_matrix=confusion_matrix, display_labels=labels)
disp.plot(include_values=True, cmap="viridis", ax=None, xticks_rotation="vertical")
plt.show()