StackingRegressor：一个简单的堆叠回归实现

一个用于叠加回归的集成学习元回归器

# 堆叠回归器

堆叠回归器是一种机器学习集成方法，它结合多个回归模型，以提高预测的准确性。该方法通过先训练多个基础回归模型，然后将它们的预测结果作为输入传递给一个最终的回归模型，从而实现更好的性能。

以下是使用 `mlxtend` 库中的 `StackingRegressor` 进行堆叠回归的基本示例：

```python
from mlxtend.regressor import StackingRegressor



## 概述


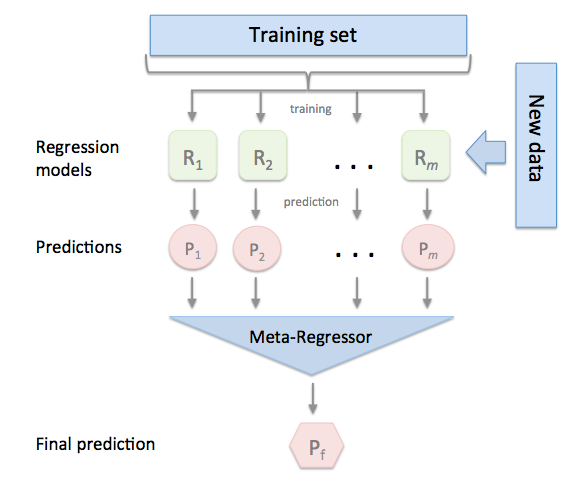
堆叠回归是一种集成学习技术，通过元回归器组合多个回归模型。单个回归模型基于完整的训练集进行训练；然后，元回归器基于集成中单个回归模型的输出（即元特征）进行拟合。


![](./StackingRegressor_files/stackingregression_overview.png)


### 参考文献


- Breiman, Leo. "[堆叠回归。](https://link.springer.com/article/10.1023/A:1018046112532#page-1)" 机器学习 24.1 (1996): 49-64.


## 示例 1 - 简单堆叠回归



```python
from mlxtend.regressor import StackingRegressor
from mlxtend.data import boston_housing_data
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.svm import SVR
import matplotlib.pyplot as plt
import numpy as np
import warnings

warnings.simplefilter('ignore')

# 生成样本数据集
np.random.seed(1)
X = np.sort(5 * np.random.rand(40, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - np.random.rand(8))


# 正在初始化模型

lr = LinearRegression()
svr_lin = SVR(kernel='linear')
ridge = Ridge(random_state=1)
svr_rbf = SVR(kernel='rbf')

stregr = StackingRegressor(regressors=[svr_lin, lr, ridge], 
                           meta_regressor=svr_rbf)

# 训练堆叠分类器

stregr.fit(X, y)
stregr.predict(X)

# 评估并可视化拟合效果

print("Mean Squared Error: %.4f"
      % np.mean((stregr.predict(X) - y) ** 2))
print('Variance Score: %.4f' % stregr.score(X, y))

with plt.style.context(('seaborn-whitegrid')):
    plt.scatter(X, y, c='lightgray')
    plt.plot(X, stregr.predict(X), c='darkgreen', lw=2)

plt.show()


Mean Squared Error: 0.1846
Variance Score: 0.7329

png

stregr


StackingRegressor(meta_regressor=SVR(),
                  regressors=[SVR(kernel='linear'), LinearRegression(),
                              Ridge(random_state=1)])

示例 2 - 堆叠回归和网格搜索

在这个第二个例子中，我们展示了 StackingCVRegressor 如何与 GridSearchCV 结合工作。堆叠仍然允许调整基本模型和元模型的超参数！

例如，我们可以使用 estimator.get_params().keys() 获取可调参数的完整列表。

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import Lasso

# 初始化模型

lr = LinearRegression()
svr_lin = SVR(kernel='linear')
ridge = Ridge(random_state=1)
lasso = Lasso(random_state=1)
svr_rbf = SVR(kernel='rbf')
regressors = [svr_lin, lr, ridge, lasso]
stregr = StackingRegressor(regressors=regressors, 
                           meta_regressor=svr_rbf)

params = {'lasso__alpha': [0.1, 1.0, 10.0],
          'ridge__alpha': [0.1, 1.0, 10.0],
          'svr__C': [0.1, 1.0, 10.0],
          'meta_regressor__C': [0.1, 1.0, 10.0, 100.0],
          'meta_regressor__gamma': [0.1, 1.0, 10.0]}

grid = GridSearchCV(estimator=stregr, 
                    param_grid=params, 
                    cv=5,
                    refit=True)
grid.fit(X, y)

print("Best: %f using %s" % (grid.best_score_, grid.best_params_))


Best: -0.082717 using {'lasso__alpha': 0.1, 'meta_regressor__C': 1.0, 'meta_regressor__gamma': 1.0, 'ridge__alpha': 0.1, 'svr__C': 10.0}

cv_keys = ('mean_test_score', 'std_test_score', 'params')

for r, _ in enumerate(grid.cv_results_['mean_test_score']):
    print("%0.3f +/- %0.2f %r"
          % (grid.cv_results_[cv_keys[0]][r],
             grid.cv_results_[cv_keys[1]][r] / 2.0,
             grid.cv_results_[cv_keys[2]][r]))
    if r > 10:
        break
print('...')

print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)


-9.810 +/- 6.86 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 0.1, 'svr__C': 0.1}
-9.591 +/- 6.67 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 0.1, 'svr__C': 1.0}
-9.591 +/- 6.67 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 0.1, 'svr__C': 10.0}
-9.819 +/- 6.87 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 1.0, 'svr__C': 0.1}
-9.600 +/- 6.68 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 1.0, 'svr__C': 1.0}
-9.600 +/- 6.68 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 1.0, 'svr__C': 10.0}
-9.878 +/- 6.91 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 10.0, 'svr__C': 0.1}
-9.665 +/- 6.71 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 10.0, 'svr__C': 1.0}
-9.665 +/- 6.71 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 0.1, 'ridge__alpha': 10.0, 'svr__C': 10.0}
-4.839 +/- 3.98 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 1.0, 'ridge__alpha': 0.1, 'svr__C': 0.1}
-3.986 +/- 3.16 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 1.0, 'ridge__alpha': 0.1, 'svr__C': 1.0}
-3.986 +/- 3.16 {'lasso__alpha': 0.1, 'meta_regressor__C': 0.1, 'meta_regressor__gamma': 1.0, 'ridge__alpha': 0.1, 'svr__C': 10.0}
...
Best parameters: {'lasso__alpha': 0.1, 'meta_regressor__C': 1.0, 'meta_regressor__gamma': 1.0, 'ridge__alpha': 0.1, 'svr__C': 10.0}
Accuracy: -0.08

# 评估并可视化拟合效果
print("Mean Squared Error: %.4f"
      % np.mean((grid.predict(X) - y) ** 2))
print('Variance Score: %.4f' % grid.score(X, y))

with plt.style.context(('seaborn-whitegrid')):
    plt.scatter(X, y, c='lightgray')
    plt.plot(X, grid.predict(X), c='darkgreen', lw=2)

plt.show()


Mean Squared Error: 0.1845
Variance Score: 0.7330

png

注意

StackingCVRegressor 还支持对 regressors 的网格搜索，甚至对单个基学习器进行网格搜索。当存在层混合的超参数时，GridSearchCV 将尝试按照从上到下的顺序替换超参数，即 regressors -> 单个基学习器 -> 回归器超参数。例如，给定如下的超参数网格：

params = {'randomforestregressor__n_estimators': [1, 100],
'regressors': [(regr1, regr1, regr1), (regr2, regr3)]}

它将首先使用 (regr1, regr2, regr3) 或 (regr2, regr3) 的实例设置。然后，它将根据 'randomforestregressor__n_estimators': [1, 100] 替换对应回归器的 'n_estimators' 设置。

API

StackingRegressor(regressors, meta_regressor, verbose=0, use_features_in_secondary=False, store_train_meta_features=False, refit=True, multi_output=False)

A Stacking regressor for scikit-learn estimators for regression.

Parameters

Attributes

Examples

For usage examples, please see https://rasbt.github.io/mlxtend/user_guide/regressor/StackingRegressor/

Methods

fit(X, y, sample_weight=None)

Learn weight coefficients from training data for each regressor.

Parameters

Returns

fit_transform(X, y=None, fit_params)

Fit to data, then transform it.

Fits transformer to `X` and `y` with optional parameters `fit_params`
and returns a transformed version of `X`.

Parameters

Returns

get_params(deep=True)

Return estimator parameter names for GridSearch support.

predict(X)

Predict target values for X.

Parameters

Returns

predict_meta_features(X)

Get meta-features of test-data.

Parameters

Returns

score(X, y, sample_weight=None)

Return the coefficient of determination :math:R^2 of the prediction.

The coefficient :math:`R^2` is defined as :math:`(1 - \frac{u}{v})`,
where :math:`u` is the residual sum of squares ``((y_true - y_pred)

2).sum()and :math:`v` is the total sum of squares((y_true - y_true.mean()) 2).sum()``. The best possible score is 1.0 and it

can be negative (because the model can be arbitrarily worse). A

constant model that always predicts the expected value of y, disregarding the input features, would get a :math:R^2 score of 0.0.

Parameters

Returns

Notes

The :math:R^2 score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of :func:~sklearn.metrics.r2_score. This influences the score method of all the multioutput regressors (except for :class:~sklearn.multioutput.MultiOutputRegressor).

set_params(params)

Set the parameters of this estimator.

Valid parameter keys can be listed with ``get_params()``.

Returns

self

Properties

coef_

None

intercept_

None

named_regressors

None

ython