教程#
本指南可以帮助你开始使用 NetworkX。
创建图#
创建一个没有节点和边的空图。
import networkx as nx
G = nx.Graph()
根据定义,{class} Graph 是一组节点(顶点)以及节点对(称为边、链接等)。在 NetworkX 中,节点可以是任何 {py:term} hashable 对象,例如文本字符串、图像、XML 对象、另一个图、自定义节点对象等。
Note
Python 的 None 对象不能用作节点。它用于确定许多函数中是否分配了可选函数参数。
节点#
图 G 可以通过多种方式扩展。NetworkX 包含许多 {doc} 图生成函数 <reference/generators> 和 {doc} 读取和写入多种格式的图的工具 <reference/readwrite/index> 。为了开始,我们先来看一些简单的操作。你可以一次添加一个节点,
G.add_node(1)
或者从任何 {py:term} iterable 容器中添加节点,例如列表
G.add_nodes_from([2, 3])
你还可以添加带有节点属性的节点,如果你的容器产生 (node, node_attribute_dict) 形式的 2 元组:
G.add_nodes_from([(4, {"color": "red"}), (5, {"color": "green"})])
节点属性将在 {ref} 下文 <attributes> 进一步讨论。
一个图中的节点可以被合并到另一个图中:
H = nx.path_graph(10)
G.add_nodes_from(H)
G 现在包含 H 的节点,作为 G 的节点。相比之下,你可以使用图 H 作为 G 中的一个节点。
G.add_node(H)
图 G 现在包含 H 作为一个节点。这种灵活性非常强大,因为它允许图的图、文件的图、函数的图等等。值得考虑如何构建你的应用程序,使节点成为有用的实体。当然,如果你愿意,也可以在 G 中使用唯一标识符,并有一个按标识符键控的单独字典来存储节点信息。
Note
如果哈希值依赖于节点对象的内容,则不应更改节点对象。
边#
G 还可以通过一次添加一条边来扩展,
G.add_edge(1, 2)
e = (2, 3)
G.add_edge(*e) # 解包边元组*
通过添加边的列表,
G.add_edges_from([(1, 2), (1, 3)])
或通过添加任何 {term} ebunch 的边。ebunch 是任何边元组的可迭代容器。边元组可以是节点的 2 元组或节点的 3 元组,后跟边属性字典,例如 (2, 3, {'weight': 3.1415}) 。边属性将在 {ref} 下文 <attributes> 进一步讨论。
G.add_edges_from(H.edges)
添加现有节点或边时没有问题。例如,在移除所有节点和边之后,
G.clear()
我们添加新节点/边,NetworkX 安静地忽略已存在的任何节点/边。
G.add_edges_from([(1, 2), (1, 3)])
G.add_node(1)
G.add_edge(1, 2)
G.add_node("spam") # 添加节点 "spam"
G.add_nodes_from("spam") # 添加 4 个节点:'s', 'p', 'a', 'm'
G.add_edge(3, 'm')
此时,图 G 包含 8 个节点和 3 条边,如下所示:
G.number_of_nodes()
8
G.number_of_edges()
3
Note
邻接报告的顺序(例如 {meth} G.adj <networkx.Graph.adj> ,{meth} G.successors <networkx.DiGraph.successors> ,{meth} G.predecessors <networkx.DiGraph.predecessors> )是边添加的顺序。然而,G.edges 的顺序是包括节点顺序和每个节点邻接关系的顺序。见下例:
DG = nx.DiGraph()
DG.add_edge(2, 1) # 按顺序添加节点 2, 1
DG.add_edge(1, 3)
DG.add_edge(2, 4)
DG.add_edge(1, 2)
assert list(DG.successors(2)) == [1, 4]
assert list(DG.edges) == [(2, 1), (2, 4), (1, 3), (1, 2)]
检查图的元素#
我们可以检查节点和边。四个基本图属性有助于报告: G.nodes , G.edges , G.adj 和 G.degree 。这些是图中节点、边、邻居(邻接关系)和节点度数的类似集合的视图。它们提供了对图结构的不断更新的只读视图。它们也类似字典,你可以通过视图查找节点和边的数据属性,并使用 .items() , .data() 方法迭代数据属性。如果你想要特定的容器类型而不是视图,可以指定一个。在这里,我们使用列表,虽然在其他情况下集合、字典、元组和其他容器可能更好。
list(G.nodes)
[1, 2, 3, 'spam', 's', 'p', 'a', 'm']
list(G.edges)
[(1, 2), (1, 3), (3, 'm')]
list(G.adj[1]) # 或者 list(G.neighbors(1))
[2, 3]
G.degree[1] # 节点 1 的边的数量
2
可以使用 {term} nbunch 来报告部分节点的边和度。nbunch 可以是: None (表示所有节点),一个节点,或不是图中的节点的可迭代节点容器。
G.edges([2, 'm'])
EdgeDataView([(2, 1), ('m', 3)])
G.degree([2, 3])
DegreeView({2: 1, 3: 2})
从图中移除元素#
可以以类似于添加的方式从图中移除节点和边。使用方法 {meth} Graph.remove_node ,{meth} Graph.remove_nodes_from ,{meth} Graph.remove_edge 和 {meth} Graph.remove_edges_from ,例如
G.remove_node(2)
G.remove_nodes_from("spam")
list(G.nodes)
[1, 3, 'spam']
G.remove_edge(1, 3)
list(G)
[1, 3, 'spam']
使用图构造函数#
图对象不必逐渐构建 - 可以将指定图结构的数据直接传递给各种图类的构造函数。通过实例化一个图类创建图结构时,可以以多种格式指定数据。
G.add_edge(1, 2)
H = nx.DiGraph(G) # 使用 G 的连接创建一个 DiGraph
list(H.edges())
[(1, 2), (2, 1)]
edgelist = [(0, 1), (1, 2), (2, 3)]
H = nx.Graph(edgelist) # 从边列表创建一个图
list(H.edges())
[(0, 1), (1, 2), (2, 3)]
adjacency_dict = {0: (1, 2), 1: (0, 2), 2: (0, 1)}
H = nx.Graph(adjacency_dict) # 创建一个将节点映射到邻居的 Graph 字典
list(H.edges())
[(0, 1), (0, 2), (1, 2)]
使用哪些作为节点和边#
你可能注意到节点和边没有被指定为 NetworkX 对象。这让你可以自由使用有意义的项目作为节点和边。最常见的选择是数字或字符串,但节点可以是任何哈希对象(除了 None ),边可以与任何对象 x 相关联,使用 G.add_edge(n1, n2, object=x) 。
例如, n1 和 n2 可以是 RCSB Protein Data Bank 的蛋白质对象, x 可以指代一个 XML 记录,详细记录它们相互作用的实验观察结果。
我们发现这种能力非常有用,但滥用它会导致意外行为,除非熟悉 Python。如果有疑问,请考虑使用 {func} ~relabel.convert_node_labels_to_integers 获取一个带有整数标签的更传统的图。
访问边和邻居#
除了 {attr} Graph.edges 和 {attr} Graph.adj 视图外,还可以使用下标表示法访问边和邻居。
G = nx.Graph([(1, 2, {"color": "yellow"})])
G[1] # 等同于 G.adj[1]
AtlasView({2: {'color': 'yellow'}})
G[1][2]
{'color': 'yellow'}
G.edges[1, 2]
{'color': 'yellow'}
如果边已经存在,可以使用下标表示法获取/设置边的属性。
G.add_edge(1, 3)
G[1][3]['color'] = "blue"
G.edges[1, 2]['color'] = "red"
G.edges[1, 2]
{'color': 'red'}
快速检查所有(节点,邻接关系)对可以使用 G.adjacency() 或 G.adj.items() 。注意,对于无向图,邻接迭代每条边两次。
FG = nx.Graph()
FG.add_weighted_edges_from([(1, 2, 0.125), (1, 3, 0.75), (2, 4, 1.2), (3, 4, 0.375)])
for n, nbrs in FG.adj.items():
for nbr, eattr in nbrs.items():
wt = eattr['weight']
if wt < 0.5: print(f"({n}, {nbr}, {wt:.3})")
(1, 2, 0.125)
(2, 1, 0.125)
(3, 4, 0.375)
(4, 3, 0.375)
通过 edges 属性方便地访问所有边。
for (u, v, wt) in FG.edges.data('weight'):
if wt < 0.5:
print(f"({u}, {v}, {wt:.3})")
(1, 2, 0.125)
(3, 4, 0.375)
向图、节点和边添加属性#
可以将权重、标签、颜色或任何你喜欢的 Python 对象附加到图、节点或边。
每个图、节点和边都可以在关联的属性字典中保存键/值属性对(键必须是可哈希的)。默认情况下,这些是空的,但可以使用 add_edge , add_node 或直接操作图 G 的属性字典 G.graph , G.nodes 和 G.edges 来添加或更改属性。
图属性#
在创建新图时分配图属性
G = nx.Graph(day="Friday")
G.graph
{'day': 'Friday'}
或者你可以稍后修改属性
G.graph['day'] = "Monday"
G.graph
{'day': 'Monday'}
节点属性#
使用 add_node() , add_nodes_from() 或 G.nodes 添加节点属性
G.add_node(1, time='5pm')
G.add_nodes_from([3], time='2pm')
G.nodes[1]
{'time': '5pm'}
G.nodes[1]['room'] = 714
G.nodes.data()
NodeDataView({1: {'time': '5pm', 'room': 714}, 3: {'time': '2pm'}})
注意,添加节点到 G.nodes 不会将其添加到图中,使用 G.add_node() 添加新节点。同样适用于边。
边属性#
使用 add_edge() , add_edges_from() 或下标表示法添加/更改边属性。
G.add_edge(1, 2, weight=4.7 )
G.add_edges_from([(3, 4), (4, 5)], color='red')
G.add_edges_from([(1, 2, {'color': 'blue'}), (2, 3, {'weight': 8})])
G[1][2]['weight'] = 4.7
G.edges[3, 4]['weight'] = 4.2
特别属性 weight 应该是数字,因为它被需要加权边的算法使用。
有向图#
{class} DiGraph 类提供特定于有向边的附加方法和属性,例如,{attr} DiGraph.out_edges ,{attr} DiGraph.in_degree ,{meth} DiGraph.predecessors ,{meth} DiGraph.successors 等。为了让算法容易同时适用于两类图,有向图的 {meth} neighbors <DiGraph.neighbors> 等同于 {meth} successors <DiGraph.successors> ,而 {attr} DiGraph.degree 报告 {attr} DiGraph.in_degree 和 {attr} DiGraph.out_degree 的总和,即使这有时感觉不一致。
DG = nx.DiGraph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])
DG.out_degree(1, weight='weight')
0.5
DG.degree(1, weight='weight')
1.25
list(DG.successors(1))
[2]
list(DG.neighbors(1))
[2]
一些算法仅适用于有向图,而其他算法在有向图上没有良好定义。实际上,将有向图和无向图混在一起是危险的。如果你想在某些测量中将有向图视为无向图,可能应该使用 {meth} Graph.to_undirected 或
H = nx.Graph(G) # 从有向图 G 创建一个无向图 H
多重图#
NetworkX 提供了允许任何节点对之间多条边的图类。{class} MultiGraph 和 {class} MultiDiGraph 类允许你两次添加同一条边,可能带有不同的边数据。这对于某些应用来说非常强大,但许多算法在这种图上没有良好定义。在结果有良好定义的地方,例如 {meth} MultiGraph.degree ,我们提供了该函数。否则,你应该以使测量有良好定义的方式转换为标准图。
MG = nx.MultiGraph()
MG.add_weighted_edges_from([(1, 2, 0.5), (1, 2, 0.75), (2, 3, 0.5)])
dict(MG.degree(weight='weight'))
{1: 1.25, 2: 1.75, 3: 0.5}
GG = nx.Graph()
for n, nbrs in MG.adjacency():
for nbr, edict in nbrs.items():
minvalue = min([d['weight'] for d in edict.values()])
GG.add_edge(n, nbr, weight = minvalue)
nx.shortest_path(GG, 1, 3)
[1, 2, 3]
图生成器和图操作#
除了逐节点或逐边构建图外,还可以通过以下方式生成图
1. 应用经典图操作,例如:#
|
返回在nbunch中的节点上诱导的子图。 |
|
合并图 G 和 H。节点的名称必须是唯一的。 |
|
合并图 G 和 H。假设节点是唯一的(不相交的)。 |
|
返回 G 和 H 的笛卡尔积。 |
|
将图G和H组合成一个单一的图,合并节点和边。 |
|
返回图 G 的补图。 |
|
返回一个图 G 的副本,其中所有边均被移除。 |
|
返回图 |
|
返回图 |
2. 调用一个经典的小图,例如,#
|
返回 Petersen 图。 |
|
返回Tutte图。 |
|
返回一个带有环的小迷宫。 |
|
返回3-正则的柏拉图四面体图。 |
3. 使用一个经典图的(构造)生成器,例如,#
|
返回具有 n 个节点的完全图 |
|
返回完整的二分图 |
|
返回杠铃图:两个完全图通过一条路径连接。 |
|
返回棒棒糖图; |
如下:
K_5 = nx.complete_graph(5)
K_3_5 = nx.complete_bipartite_graph(3, 5)
barbell = nx.barbell_graph(10, 10)
lollipop = nx.lollipop_graph(10, 20)
4. 使用随机图生成器,例如,#
|
返回一个 \(G_{n,p}\) 随机图,也称为 Erdős-Rényi 图或二项图。 |
|
返回一个 Watts–Strogatz 小世界图。 |
|
返回一个使用Barabási–Albert优先连接的随机图 |
|
返回一个随机的龙虾图。 |
如下:
er = nx.erdos_renyi_graph(100, 0.15)
ws = nx.watts_strogatz_graph(30, 3, 0.1)
ba = nx.barabasi_albert_graph(100, 5)
red = nx.random_lobster(100, 0.9, 0.9)
5. 使用常见图格式读取存储在文件中的图#
NetworkX 支持多种流行格式,例如边列表、邻接列表、GML、GraphML、LEDA 等。
nx.write_gml(red, "path.to.file")
mygraph = nx.read_gml("path.to.file")
有关图格式的详细信息,请参见 {doc} /reference/readwrite/index ,有关图生成函数,请参见 {doc} /reference/generators
分析图#
可以使用各种图论函数分析 G 的结构,例如:
G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3)])
G.add_node("spam") # 添加节点 "spam"
list(nx.connected_components(G))
[{1, 2, 3}, {'spam'}]
sorted(d for n, d in G.degree())
[0, 1, 1, 2]
nx.clustering(G)
{1: 0, 2: 0, 3: 0, 'spam': 0}
具有大输出量的一些函数迭代(节点,值)2 元组。如果需要,可以轻松地将这些存储在 dict 结构中。
sp = dict(nx.all_pairs_shortest_path(G))
sp[3]
{3: [3], 1: [3, 1], 2: [3, 1, 2]}
有关支持的图算法的详细信息,请参见 {doc} /reference/algorithms/index 。
绘制图#
NetworkX 不是主要的图绘制软件包,但包括使用 Matplotlib 的基本绘图以及使用开源 Graphviz 软件包的接口。这些是 {doc} networkx.drawing <reference/drawing> 模块的一部分,如果可能,将被导入。
首先导入 Matplotlib 的绘图接口(pylab 也可用)
import matplotlib.pyplot as plt
要测试 ~networkx.drawing.nx_pylab 导入是否成功,可以使用以下命令绘制 G
G = nx.petersen_graph()
subax1 = plt.subplot(121)
nx.draw(G, with_labels=True, font_weight='bold')
subax2 = plt.subplot(122)
nx.draw_shell(G, nlist=[range(5, 10), range(5)], with_labels=True, font_weight='bold')
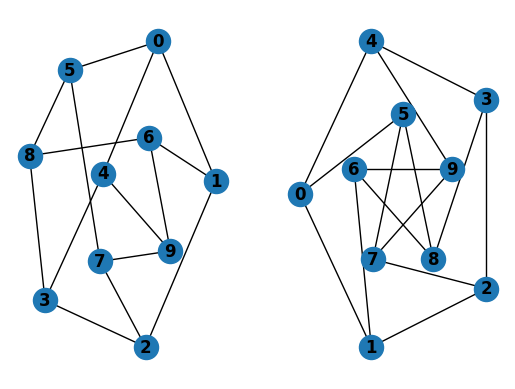
在绘制到交互显示时。请注意,如果不在交互模式下使用 matplotlib,可能需要发出一个 Matplotlib 命令
plt.show()
options = {
'node_color': 'black',
'node_size': 100,
'width': 3,
}
subax1 = plt.subplot(221)
nx.draw_random(G, **options)
subax2 = plt.subplot(222)
nx.draw_circular(G, **options)
subax3 = plt.subplot(223)
nx.draw_spectral(G, **options)
subax4 = plt.subplot(224)
nx.draw_shell(G, nlist=[range(5,10), range(5)], **options)
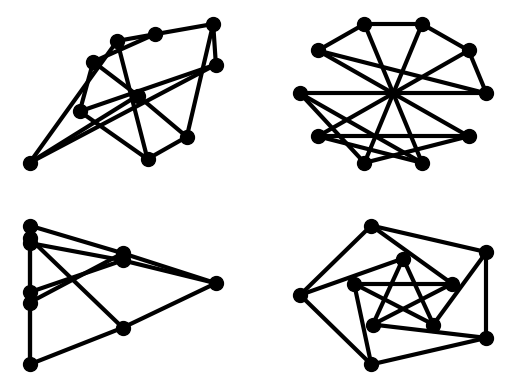
可以通过 {func} ~drawing.nx_pylab.draw_networkx 发现更多选项,并通过 {mod} 布局模块 <networkx.drawing.layout> 发现布局选项。可以使用多个壳来进行 {func} ~drawing.nx_pylab.draw_shell 。
G = nx.dodecahedral_graph()
shells = [[2, 3, 4, 5, 6], [8, 1, 0, 19, 18, 17, 16, 15, 14, 7], [9, 10, 11, 12, 13]]
nx.draw_shell(G, nlist=shells, **options)
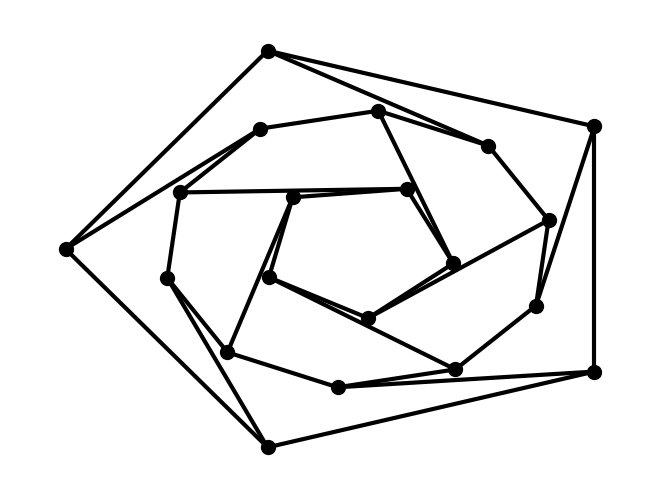
要将图保存到文件中,请使用例如
>>> nx.draw(G)
>>> plt.savefig("path.png")
此函数将图写入本地目录中的文件 path.png 。如果系统上有 Graphviz 和 PyGraphviz 或 pydot,可以使用 networkx.drawing.nx_agraph.graphviz_layout 或 networkx.drawing.nx_pydot.graphviz_layout 获取节点位置,或以 dot 格式写入图以供进一步处理。
>>> from networkx.drawing.nx_pydot import write_dot
>>> pos = nx.nx_agraph.graphviz_layout(G)
>>> nx.draw(G, pos=pos)
>>> write_dot(G, 'file.dot')
有关详细信息,请参见 {doc} /reference/drawing 。
NX 指南#
如果你对学习更多关于 NetworkX、图论和网络分析感兴趣,可以查看 {doc} nx-guides <nx-guides:index> 。在那里,你可以找到教程、真实世界的应用和深入的图和网络算法的研究。所有材料都是官方的,由 NetworkX 社区开发和策划。
