pymc.HyperGeometric

class pymc.HyperGeometric(name, *args, **kwargs)

离散超几何分布。

在一系列 \(n\) 次伯努利试验中，从包含 \(k\) 个好（或成功或I型）对象的 \(N\) 个对象的总体中无放回地抽取，成功次数为 \(x\) 的概率。此分布的概率质量函数为

\[f(x \mid N, n, k) = \frac{\binom{k}{x}\binom{N-k}{n-x}}{\binom{N}{n}}\]

(Source code, png, hires.png, pdf)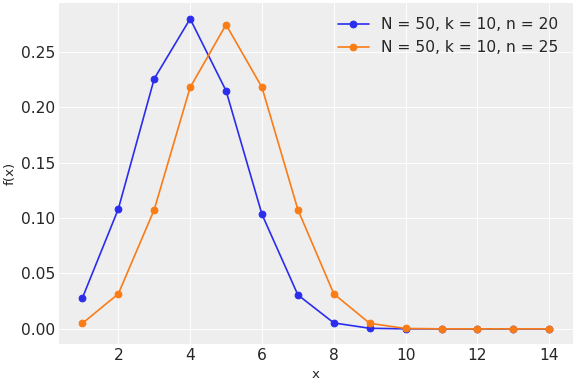

支持	\(x \in \left[\max(0, n - N + k), \min(k, n)\right]\)
均值	\(\dfrac{nk}{N}\)
方差	\(\dfrac{(N-n)nk(N-k)}{(N-1)N^2}\)

参数:

N : 类似张量 的 intpython:int 的 tensor_like

总人口规模（N > 0）

k : 类似张量 的 intpython:int 的 tensor_like

人口中成功个体的数量（0 <= k <= N）

n : 类似张量 的 intpython:int 的 tensor_like

从总体中抽取的样本数量（0 <= n <= N）

方法

HyperGeometric.dist(N, k, n, *args, **kwargs)

创建一个与 cls 分布相对应的张量变量。