PyMC 和 PyTensor#
作者: Ricardo Vieira 和 Juan Orduz
在本笔记本中,我们想介绍 PyMC 模型如何转化为 PyTensor 图。目的不是对 pytensor 的所有功能进行详细描述,而是关注理解它与 PyMC 之间关联的主要概念。有关该项目的更详细描述,请参考官方文档。
准备笔记本#
首先导入所需的库。
import pytensor
import pytensor.tensor as pt
import pymc as pm
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats
PyTensor简介#
我们首先来了解一下pytensor。根据他们的文档
PyTensor是一个Python库,可以让用户定义、优化和高效计算涉及多维数组的数学表达式。
一个简单的例子#
首先,我们定义一些pytensor张量,并展示如何执行一些基本操作。
x = pt.scalar(name="x")
y = pt.vector(name="y")
print(
f"""
x 类型: {x.type}
x 名称 = {x.name}
---
y 类型: {y.type}
y 名称 = {y.name}
"""
)
x type: TensorType(float64, ())
x name = x
---
y type: TensorType(float64, (?,))
y name = y
现在我们已经定义了x和y张量,我们可以通过将它们相加来创建一个新的张量。
z = x + y
z.name = "x + y"
为了使计算稍微复杂一些,让我们对结果张量取对数。
w = pt.log(z)
w.name = "log(x + y)"
我们可以使用 dprint() 函数打印任何给定张量的计算图。
pytensor.dprint(w)
Elemwise{log,no_inplace} [id A] 'log(x + y)'
|Elemwise{add,no_inplace} [id B] 'x + y'
|InplaceDimShuffle{x} [id C]
| |x [id D]
|y [id E]
<ipykernel.iostream.OutStream at 0x216736585b0>
请注意,此图形尚未进行任何计算!它仅仅是在定义要执行的步骤序列。我们可以使用 function() 来定义一个可调用对象,以便我们可以通过图形传递值。
f = pytensor.function(inputs=[x, y], outputs=w)
现在图表已经编制完成,我们可以输入一些具体的数值:
f(x=0, y=[1, np.e])
array([0., 1.])
小技巧
有时我们只是想进行调试,可以使用 eval() 来做到这一点:
w.eval({x: 0, y: [1, np.e]})
array([0., 1.])
您也可以设置中间值。
w.eval({z: [1, np.e]})
array([0., 1.])
PyTensor 是聪明的!#
pytensor 最重要的特点之一是它可以自动优化图中的数学运算。让我们考虑一个简单的例子:
a = pt.scalar(name="a")
b = pt.scalar(name="b")
c = a / b
c.name = "a / b"
pytensor.dprint(c)
Elemwise{true_div,no_inplace} [id A] 'a / b'
|a [id B]
|b [id C]
<ipykernel.iostream.OutStream at 0x216736585b0>
现在让我们将 b 乘以 c。这应该简单地得到 a。
d = b * c
d.name = "b * c"
pytensor.dprint(d)
Elemwise{mul,no_inplace} [id A] 'b * c'
|b [id B]
|Elemwise{true_div,no_inplace} [id C] 'a / b'
|a [id D]
|b [id B]
<ipykernel.iostream.OutStream at 0x216736585b0>
该图显示了完整的计算,但一旦我们编译它,操作就变成了对 a 的恒等操作,正如预期的那样。
g = pytensor.function(inputs=[a, b], outputs=d)
pytensor.dprint(g)
DeepCopyOp [id A] 'a' 0
|a [id B]
<ipykernel.iostream.OutStream at 0x216736585b0>
PyTensor图中包含什么?#
下图显示了pytensor图的基本结构。
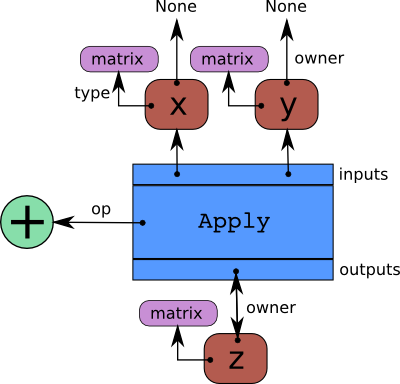
我们可以通过在上述部分的第一个示例中明确指出这些概念,使它们变得更加具体。让我们计算张量 z 的图组件。
print(
f"""
z 类型: {z.type}
z 名称 = {z.name}
z 所有者 = {z.owner}
z 所有者输入 = {z.owner.inputs}
z 所有者操作 = {z.owner.op}
z 所有者输出 = {z.owner.outputs}
"""
)
z type: TensorType(float64, (?,))
z name = x + y
z owner = Elemwise{add,no_inplace}(InplaceDimShuffle{x}.0, y)
z owner inputs = [InplaceDimShuffle{x}.0, y]
z owner op = Elemwise{add,no_inplace}
z owner output = [x + y]
以下代码片段帮助我们理解这些概念,通过分析 w 的计算图。实际代码在这里并不是最重要的,重点是输出结果。
# 从顶部开始
stack = [w]
while stack:
print("---")
var = stack.pop(0)
print(f"Checking variable {var} of type {var.type}")
# 检查变量不是根变量
if var.owner is not None:
print(f" > Op is {var.owner.op}")
# 遍历输入
for i, input in enumerate(var.owner.inputs):
print(f" > Input {i} is {input}")
stack.append(input)
else:
print(f" > {var} is a root variable")
---
Checking variable log(x + y) of type TensorType(float64, (?,))
> Op is Elemwise{log,no_inplace}
> Input 0 is x + y
---
Checking variable x + y of type TensorType(float64, (?,))
> Op is Elemwise{add,no_inplace}
> Input 0 is InplaceDimShuffle{x}.0
> Input 1 is y
---
Checking variable InplaceDimShuffle{x}.0 of type TensorType(float64, (1,))
> Op is InplaceDimShuffle{x}
> Input 0 is x
---
Checking variable y of type TensorType(float64, (?,))
> y is a root variable
---
Checking variable x of type TensorType(float64, ())
> x is a root variable
请注意,这与上述引入的 dprint() 函数的输出非常相似。
pytensor.dprint(w)
Elemwise{log,no_inplace} [id A] 'log(x + y)'
|Elemwise{add,no_inplace} [id B] 'x + y'
|InplaceDimShuffle{x} [id C]
| |x [id D]
|y [id E]
<ipykernel.iostream.OutStream at 0x216736585b0>
图形操作 101#
PyTensor的另一个有趣功能是能够操作计算图,这是在TensorFlow或PyTorch中无法实现的。在这里,我们继续上面的例子,以便说明这一技术的主要思想。
# 获取输入张量
list(pytensor.graph.graph_inputs(graphs=[w]))
[x, y]
作为一个简单的例子,让我们在 log() 之前添加一个 exp() (以获得恒等函数)。
parent_of_w = w.owner.inputs[0] # 获取z张量
new_parent_of_w = pt.exp(parent_of_w) # 修改w的父节点
new_parent_of_w.name = "exp(x + y)"
注意到w的图形实际上并没有改变:
pytensor.dprint(w)
Elemwise{log,no_inplace} [id A] 'log(x + y)'
|Elemwise{add,no_inplace} [id B] 'x + y'
|InplaceDimShuffle{x} [id C]
| |x [id D]
|y [id E]
<ipykernel.iostream.OutStream at 0x216736585b0>
要修改图形,我们需要使用 clone_replace() 函数,它 返回初始子图的副本,并进行相应的替换。
new_w = pytensor.clone_replace(output=[w], replace={parent_of_w: new_parent_of_w})[0]
new_w.name = "log(exp(x + y))"
pytensor.dprint(new_w)
Elemwise{log,no_inplace} [id A] 'log(exp(x + y))'
|Elemwise{exp,no_inplace} [id B] 'exp(x + y)'
|Elemwise{add,no_inplace} [id C] 'x + y'
|InplaceDimShuffle{x} [id D]
| |x [id E]
|y [id F]
<ipykernel.iostream.OutStream at 0x216736585b0>
最后,我们可以通过向新图传递一些输入来测试修改后的图。
new_w.eval({x: 0, y: [1, np.e]})
array([1. , 2.71828183])
如预期,新图仅仅是恒等函数。
备注
再一次请注意,一旦我们编译函数,pytensor 足够聪明,可以省略 exp 和 log。
f = pytensor.function(inputs=[x, y], outputs=new_w)
pytensor.dprint(f)
Elemwise{add,no_inplace} [id A] 'x + y' 1
|InplaceDimShuffle{x} [id B] 0
| |x [id C]
|y [id D]
<ipykernel.iostream.OutStream at 0x216736585b0>
f(x=0, y=[1, np.e])
array([1. , 2.71828183])
PyTensor 随机变量#
现在我们已经了解了 PyTensor 的基础知识,我们希望朝着随机变量的方向发展。
我们如何在 numpy 中生成随机数呢?为了说明这个问题,我们可以从正态分布中采样:
a = np.random.normal(loc=0, scale=1, size=1_000)
fig, ax = plt.subplots(figsize=(8, 6))
ax.hist(a, color="C0", bins=15)
ax.set(title="Samples from a normal distribution using numpy", ylabel="count");
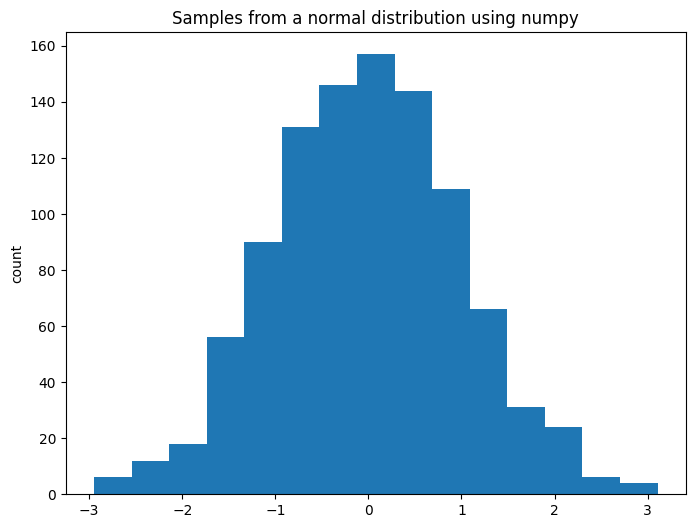
现在让我们尝试在PyTensor中进行操作。
y = pt.random.normal(loc=0, scale=1, name="y")
y.type
TensorType(float64, ())
接下来,我们使用 dprint() 显示图形。
pytensor.dprint(y)
normal_rv{0, (0, 0), floatX, False}.1 [id A] 'y'
|RandomGeneratorSharedVariable(<Generator(PCG64) at 0x2167B37F3E0>) [id B]
|TensorConstant{[]} [id C]
|TensorConstant{11} [id D]
|TensorConstant{0} [id E]
|TensorConstant{1} [id F]
<ipykernel.iostream.OutStream at 0x216736585b0>
输入始终按以下顺序提供:
rng共享变量sizedtype(数字代码)arg1arg2argn
我们可以通过对随机变量调用 eval() 来进行采样。
y.eval()
array(-1.4186441)
请注意,这些样本始终是相同的!
for i in range(10):
print(f"Sample {i}: {y.eval()}")
Sample 0: -1.4186441029543038
Sample 1: -1.4186441029543038
Sample 2: -1.4186441029543038
Sample 3: -1.4186441029543038
Sample 4: -1.4186441029543038
Sample 5: -1.4186441029543038
Sample 6: -1.4186441029543038
Sample 7: -1.4186441029543038
Sample 8: -1.4186441029543038
Sample 9: -1.4186441029543038
我们总是得到相同的样本!这与图中的随机种子步骤有关,即 RandomGeneratorSharedVariable (我们在此不深入探讨这个主题)。下面我们将展示如何使用 pymc 生成不同的样本。
请上传需要翻译的ipynb文件。
PyMC#

为此,我们首先定义一个 pymc 正态分布。
x = pm.Normal.dist(mu=0, sigma=1)
pytensor.dprint(x)
normal_rv{0, (0, 0), floatX, False}.1 [id A]
|RandomGeneratorSharedVariable(<Generator(PCG64) at 0x2167B626260>) [id B]
|TensorConstant{[]} [id C]
|TensorConstant{11} [id D]
|TensorConstant{0} [id E]
|TensorConstant{1.0} [id F]
<ipykernel.iostream.OutStream at 0x216736585b0>
注意到 x 只是一个普通的 RandomVariable,并且除了 rng 之外,它与 y 是相同的。
我们可以通过调用 eval() 以上述方式尝试生成样本。
for i in range(10):
print(f"Sample {i}: {x.eval()}")
Sample 0: 1.3064743941879295
Sample 1: 1.3064743941879295
Sample 2: 1.3064743941879295
Sample 3: 1.3064743941879295
Sample 4: 1.3064743941879295
Sample 5: 1.3064743941879295
Sample 6: 1.3064743941879295
Sample 7: 1.3064743941879295
Sample 8: 1.3064743941879295
Sample 9: 1.3064743941879295
与之前一样,我们在所有迭代中得到相同的值。生成随机样本的正确方法是使用 draw()。
fig, ax = plt.subplots(figsize=(8, 6))
ax.hist(pm.draw(x, draws=1_000), color="C1", bins=15)
ax.set(title="Samples from a normal distribution using pymc", ylabel="count");
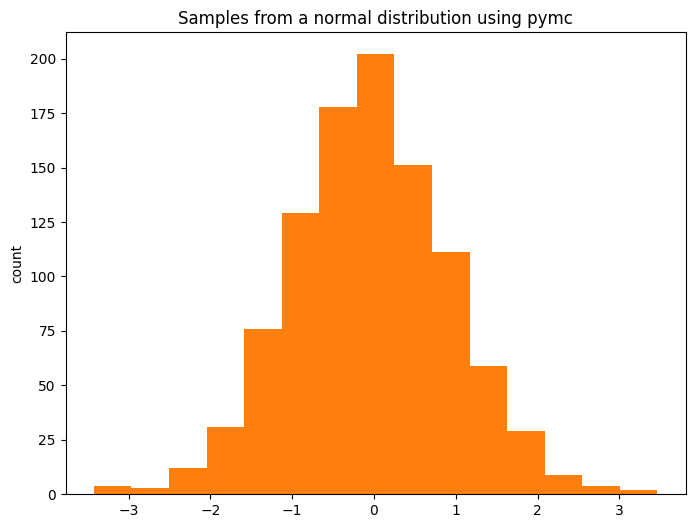
太好了!我们学会了如何从 pymc 分布中进行采样!
背后发生了什么?#
我们现在可以看看这是如何在 Model 内部完成的。
with pm.Model() as model:
z = pm.Normal(name="z", mu=np.array([0, 0]), sigma=np.array([1, 2]))
pytensor.dprint(z)
normal_rv{0, (0, 0), floatX, False}.1 [id A] 'z'
|RandomGeneratorSharedVariable(<Generator(PCG64) at 0x2167B74CD60>) [id B]
|TensorConstant{[]} [id C]
|TensorConstant{11} [id D]
|TensorConstant{(2,) of 0} [id E]
|TensorConstant{[1. 2.]} [id F]
<ipykernel.iostream.OutStream at 0x216736585b0>
我们正在创建随机变量,就像之前看到的那样,但现在将它们注册到 pymc 模型中。要提取随机变量的列表,我们可以简单地执行:
model.basic_RVs
[z ~ N(<constant>, <constant>)]
pytensor.dprint(model.basic_RVs[0])
normal_rv{0, (0, 0), floatX, False}.1 [id A] 'z'
|RandomGeneratorSharedVariable(<Generator(PCG64) at 0x2167B74CD60>) [id B]
|TensorConstant{[]} [id C]
|TensorConstant{11} [id D]
|TensorConstant{(2,) of 0} [id E]
|TensorConstant{[1. 2.]} [id F]
<ipykernel.iostream.OutStream at 0x216736585b0>
我们可以尝试通过 eval() 进行采样,正如上面所示,这样在每次迭代中我们得到相同的样本也就不足为奇了。
for i in range(10):
print(f"Sample {i}: {z.eval()}")
Sample 0: [-0.30775592 1.21469108]
Sample 1: [-0.30775592 1.21469108]
Sample 2: [-0.30775592 1.21469108]
Sample 3: [-0.30775592 1.21469108]
Sample 4: [-0.30775592 1.21469108]
Sample 5: [-0.30775592 1.21469108]
Sample 6: [-0.30775592 1.21469108]
Sample 7: [-0.30775592 1.21469108]
Sample 8: [-0.30775592 1.21469108]
Sample 9: [-0.30775592 1.21469108]
再次,正确的抽样方式是通过 draw()。
for i in range(10):
print(f"Sample {i}: {pm.draw(z)}")
Sample 0: [-1.2390824 0.3744465]
Sample 1: [0.76748461 0.95086347]
Sample 2: [-1.11985098 -1.94744586]
Sample 3: [-0.62003335 0.10075427]
Sample 4: [-0.75744869 0.69140323]
Sample 5: [-0.95472672 -1.0814984 ]
Sample 6: [-0.81052179 -2.05414581]
Sample 7: [0.37456894 1.76040717]
Sample 8: [-0.61006854 -0.05034957]
Sample 9: [1.19039658 1.10460999]
fig, ax = plt.subplots(figsize=(8, 8))
z_draws = pm.draw(vars=z, draws=10_000)
ax.hist2d(x=z_draws[:, 0], y=z_draws[:, 1], bins=25)
ax.set(title="Samples Histogram");
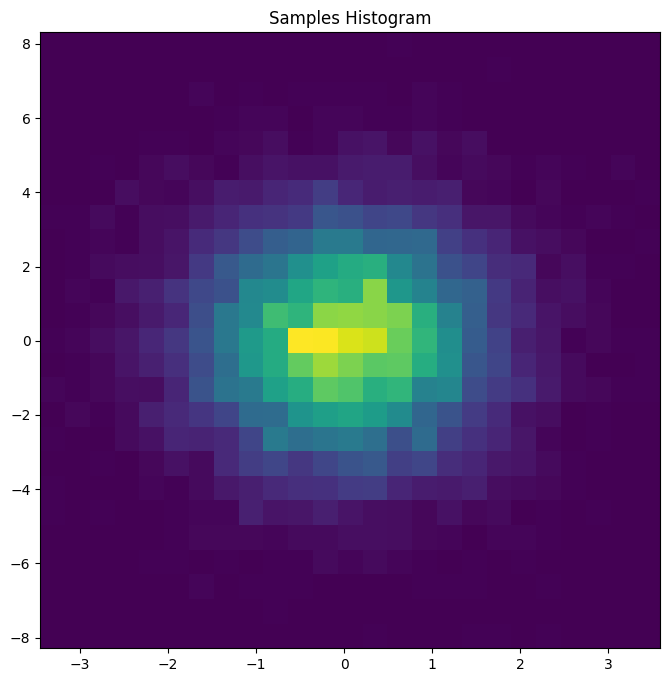
够了,随机变量,我想看看一些(对数)概率!#
回想一下我们在上面定义的以下模型:
model
pymc能够将RandomVariable转换为相应的概率函数。一种简单的方法是使用logp(),该函数的第一个输入是一个RandomVariable,第二个输入是对其进行评估的值(我们稍后将详细讨论这一点)。
z_value = pt.vector(name="z")
z_logp = pm.logp(rv=z, value=z_value)
z_logp包含表示正态随机变量z的对数概率的PyTensor图,该概率在z_value处进行评估。
pytensor.dprint(z_logp)
Check{sigma > 0} [id A] 'z_logprob'
|Elemwise{sub,no_inplace} [id B]
| |Elemwise{sub,no_inplace} [id C]
| | |Elemwise{mul,no_inplace} [id D]
| | | |InplaceDimShuffle{x} [id E]
| | | | |TensorConstant{-0.5} [id F]
| | | |Elemwise{pow,no_inplace} [id G]
| | | |Elemwise{true_div,no_inplace} [id H]
| | | | |Elemwise{sub,no_inplace} [id I]
| | | | | |z [id J]
| | | | | |TensorConstant{(2,) of 0} [id K]
| | | | |TensorConstant{[1. 2.]} [id L]
| | | |InplaceDimShuffle{x} [id M]
| | | |TensorConstant{2} [id N]
| | |InplaceDimShuffle{x} [id O]
| | |Elemwise{log,no_inplace} [id P]
| | |Elemwise{sqrt,no_inplace} [id Q]
| | |TensorConstant{6.283185307179586} [id R]
| |Elemwise{log,no_inplace} [id S]
| |TensorConstant{[1. 2.]} [id L]
|All [id T]
|MakeVector{dtype='bool'} [id U]
|All [id V]
|Elemwise{gt,no_inplace} [id W]
|TensorConstant{[1. 2.]} [id L]
|InplaceDimShuffle{x} [id X]
|TensorConstant{0} [id Y]
<ipykernel.iostream.OutStream at 0x216736585b0>
小技巧
还有一个方便的 pymc 函数可以计算随机变量的对数累积概率 logcdf()。
请注意,如开头所述,目前尚未进行任何计算。实际的计算是在编译和传递输入后进行的。为了说明目的,我们将再次使用方便的 eval() 方法。
z_logp.eval({z_value: [0, 0]})
array([-0.91893853, -1.61208571])
这无非是评估正态分布的对数概率。
scipy.stats.norm.logpdf(x=np.array([0, 0]), loc=np.array([0, 0]), scale=np.array([1, 2]))
array([-0.91893853, -1.61208571])
pymc 模型提供了一些有用的例程来便于将 RandomVariable 转换为概率函数。例如,可以使用 logp() 来提取模型中所有变量的联合概率:
pytensor.dprint(model.logp(sum=False))
Check{sigma > 0} [id A] 'z_logprob'
|Elemwise{sub,no_inplace} [id B]
| |Elemwise{sub,no_inplace} [id C]
| | |Elemwise{mul,no_inplace} [id D]
| | | |InplaceDimShuffle{x} [id E]
| | | | |TensorConstant{-0.5} [id F]
| | | |Elemwise{pow,no_inplace} [id G]
| | | |Elemwise{true_div,no_inplace} [id H]
| | | | |Elemwise{sub,no_inplace} [id I]
| | | | | |z [id J]
| | | | | |TensorConstant{(2,) of 0} [id K]
| | | | |TensorConstant{[1. 2.]} [id L]
| | | |InplaceDimShuffle{x} [id M]
| | | |TensorConstant{2} [id N]
| | |InplaceDimShuffle{x} [id O]
| | |Elemwise{log,no_inplace} [id P]
| | |Elemwise{sqrt,no_inplace} [id Q]
| | |TensorConstant{6.283185307179586} [id R]
| |Elemwise{log,no_inplace} [id S]
| |TensorConstant{[1. 2.]} [id L]
|All [id T]
|MakeVector{dtype='bool'} [id U]
|All [id V]
|Elemwise{gt,no_inplace} [id W]
|TensorConstant{[1. 2.]} [id L]
|InplaceDimShuffle{x} [id X]
|TensorConstant{0} [id Y]
<ipykernel.iostream.OutStream at 0x216736585b0>
因为我们只有一个变量,这个函数等价于我们之前手动调用 pm.logp 所得到的结果。我们还可以使用辅助函数 compile_logp() 来返回一个已经编译的模型 logp 的 PyTensor 函数。
logp_function = model.compile_logp(sum=False)
这个函数期望一个 “point” 字典作为输入。我们可以自己创建它,但为了说明另一个有用的 Model 方法,讓我們调用 initial_point(),它返回大多数采样器在决定从哪里开始采样时使用的点。
point = model.initial_point()
point
{'z': array([0., 0.])}
logp_function(point)
[array([-0.91893853, -1.61208571])]
什么是值变量,它们为什么重要?#
正如我们在上面看到的,logp 图形没有随机变量。相反,它是根据输入(值)变量定义的。当我们想进行采样时,每个随机变量(RV)都被替换为在相应输入(值)变量上评估的 logp 函数。让我们通过一些示例来看这如何工作。RV 和值变量可以在这些 scipy 操作中观察到:
rv = scipy.stats.norm(0, 1)
# Equivalent to rv = pm.Normal("rv", 0, 1)
scipy.stats.norm(0, 1)
<scipy.stats._distn_infrastructure.rv_continuous_frozen at 0x2167ce77690>
# 等同于 rv_draw = pm.draw(rv, 3)
rv.rvs(3)
array([-1.41907251, -1.01111034, -0.16152042])
# 等同于 rv_logp = pm.logp(rv, 1.25)
rv.logpdf(1.25)
-1.7001885332046727
接下来,让我们看看这些数值变量在一个稍微复杂的模型中是如何表现的。
with pm.Model() as model_2:
mu = pm.Normal(name="mu", mu=0, sigma=2)
sigma = pm.HalfNormal(name="sigma", sigma=3)
x = pm.Normal(name="x", mu=mu, sigma=sigma)
每个模型 RV 与一个“值变量”相关:
model_2.rvs_to_values
{mu ~ N(0, 2): mu, sigma ~ N**+(0, 3): sigma_log__, x ~ N(mu, sigma): x}
请注意,对于sigma,关联值是在对数尺度上,因为在实际中我们需要NUTS采样的无界值。
model_2.value_vars
[mu, sigma_log__, x]
现在我们知道如何提取模型变量,我们可以计算模型对特定值的逐元素对数概率。
# 提取值为 pytensor.tensor.var.TensorVariable
mu_value = model_2.rvs_to_values[mu]
sigma_log_value = model_2.rvs_to_values[sigma]
x_value = model_2.rvs_to_values[x]
# 模型逐元素的对数概率(我们不取和)
logp_graph = pt.stack(model_2.logp(sum=False))
# 通过传递具体值进行评估
logp_graph.eval({mu_value: 0, sigma_log_value: -10, x_value: 0})
array([ -1.61208571, -11.32440364, 9.08106147])
这相当于:
print(
f"""
mu_value -> {scipy.stats.norm.logpdf(x=0, loc=0, scale=2)}
sigma_log_value -> {- 10 + scipy.stats.halfnorm.logpdf(x=np.exp(-10), loc=0, scale=3)}
x_value -> {scipy.stats.norm.logpdf(x=0, loc=0, scale=np.exp(-10))}
"""
)
mu_value -> -1.612085713764618
sigma_log_value -> -11.324403641427345
x_value -> 9.081061466795328
注意
对于 sigma_log_value,我们添加了 \(-10\) 项以使 scipy 和 pytensor 匹配,这是因为雅可比。
正如我们已经看到的,我们也可以使用方法 compile_logp() 来获得模型 logp 的编译 pytensor 函数,该函数接受一个 {值变量名称 : 值} 的字典作为输入:
model_2.compile_logp(sum=False)({"mu": 0, "sigma_log__": -10, "x": 0})
[array(-1.61208571), array(-11.32440364), array(9.08106147)]
{class}~pymc.Model 类还具有提取对数概率梯度的方法 ({meth}~pymc.Model.dlogp) 和海森矩阵的方法 ({meth}~pymc.Model.d2logp`)。
如果您想深入了解pytensor中的随机变量和pymc分布的内部机制,请查看分布开发者指南。
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor
Last updated: Tue Dec 06 2022
Python implementation: CPython
Python version : 3.11.0
IPython version : 8.7.0
pytensor: 2.8.10
numpy : 1.23.4
scipy : 1.9.3
pymc : 4.4.0+207.g7c3068a1c
pytensor : 2.8.10
matplotlib: 3.6.2
Watermark: 2.3.1
