同构 - 如何判断两个图是否相似？#

import networkx as nx
import matplotlib.pyplot as plt

什么是同构？为什么它有趣？#

由于未标记的图可以有多种空间表示，两个图是同构的，如果它们具有相同数量的边、顶点以及相同的边连接性。让我们看一个两个同构图的例子，

plt.subplot(221)
G = nx.cubical_graph()
nx.draw_spectral(G, with_labels=True, node_color="c")
plt.title("G", fontweight="bold")
H = nx.cubical_graph()
plt.subplot(222)
nx.draw_circular(H, with_labels=True, node_color="yellow")
plt.title("H", fontweight="bold")

plt.show()

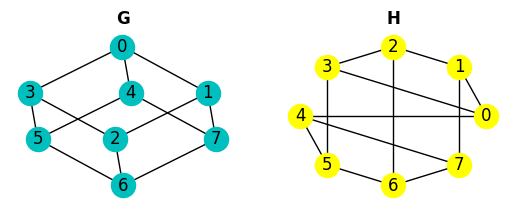
../../../_images/6a24f65fbeedbb40ae0e8b8b926a1f16e4b4c31ffab85b4dbb37146361d407e6.png

这两个图的空间表示非常不同，但它们是相同的图！

正式定义#

G 和 H 是同构的，如果我们能在 G 和 H 的顶点集之间建立一个双射。

\[ {\displaystyle f\colon N(G)\to N(H)} \]

例如，如果

\(v\) 和 \(w\) 在 G 中相邻 \(\iff\) \(f(v)\) 和 \(f(w)\) 在 H 中相邻

为了正式证明两个图是同构的，我们需要找到顶点集之间的双射。对于前面的例子，那将是：

\[f(i) = i+1 \hspace{0.5cm} \forall i \in [0, 7]\]

对于小例子，同构可能看起来很容易。但这不是一个简单的问题。对于两个具有 n 个节点的图 G 和 H，有 n! 种可能的双射函数。检查每一种组合对于更大的图来说不是一个可行的选项。事实上，同构是 NP 问题的一部分。这意味着我们不知道任何在多项式时间内运行的算法。

应用#

图同构问题有很多应用。

图像识别：图像可以转换为图，通过找到（子）同构，我们可以比较两张图像是否相似。
验证电子电路和通信网络设计的不同表示的等价性。
识别化学化合物和蛋白质。
指纹、面部和视网膜匹配的算法。
社交网络上的聚类算法。

同构算法#

朴素方法

有一些初始属性我们可以检查，以决定是否可能存在同构

G 和 H 必须具有相同数量的节点和边
G 和 H 的度序列必须相同

这些是必要条件，但不能保证两个图是同构的。让我们看一个小例子：

plt.subplot(221)
G = nx.cycle_graph(6)
nx.draw_circular(G)
plt.title("G", fontweight="bold")
plt.subplot(222)
H = nx.union(nx.cycle_graph(3), nx.cycle_graph(3), rename=("s", "d"))
nx.draw_circular(H, node_color="r")
plt.title("H", fontweight="bold")
plt.show()

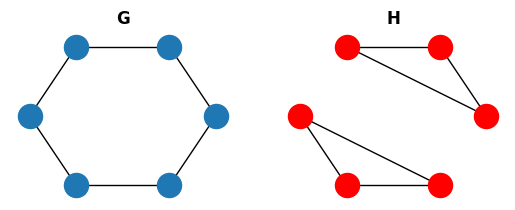
../../../_images/a166e6536ba2a0bec62eec96bc2a6c497029b102f8f1d78dff52c2400094fe02.png

我们可以使用函数 nx.faster_could_be_isomorphic() 来检查 G 和 H 是否具有相同的度序列。

nx.faster_could_be_isomorphic(G, H)

True

这些图显然不是同构的，但它们具有相同的度序列。

我们可以检查的另一个属性是：

具有相同数量的特定长度的环，例如三角形。

我们可以使用函数 nx.fast_could_be_isomorphic() 来检查图是否具有相同的度和三角形序列。三角形序列包含每个节点所属的三角形数量。

nx.fast_could_be_isomorphic(G, H)

False

这个新属性使我们能够检测到前面例子中的图不是同构的。

我们可以进一步检查：

相同数量的最大团。

我们可以使用函数 nx.could_be_isomorphic() 来检查图是否具有相同的度、三角形和团序列。团序列包含每个节点所属的最大团数量。

nx.could_be_isomorphic(G, H)

False

再次我们可以检测到 G 和 H 不是同构的。但这些条件不足以说两个图是同构的。让我们看下面的例子：

plt.subplot(221)
G = nx.path_graph(5)
G.add_edge(2, 5)
nx.draw_circular(G, with_labels=True, node_color="g")
plt.title("G", fontweight="bold")

plt.subplot(222)
H = nx.path_graph(5)
H.add_edge(3, 5)
nx.draw_circular(H, with_labels=True, node_color="c")
plt.title("H", fontweight="bold")
plt.show()

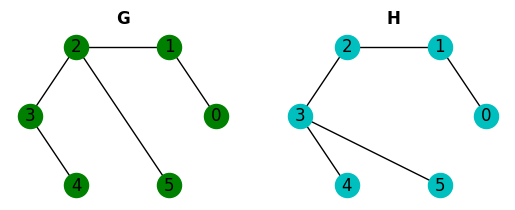
../../../_images/91ecf393203a53c0ea7c15c0f3e6b40bab76992d91aca81c9bc1273ec22e6181.png

nx.could_be_isomorphic(G, H)

True

这些图满足所有必要条件，但它们不是同构的。

一些在多项式时间内可解的图类#

树
平面图（实际上，平面图同构是 O(log(n))）
区间图
排列图
循环图
有界参数图
- 有界树宽度的图
- 有界亏格的图
- 度有界图
- 特征值重数有界图
- k-可收缩图（有界度和有界亏格的推广）

让我们看一个例子，我们可以使用同构模块中的函数 tree_isomorphism() 来检查两棵树是否同构，时间复杂度为 \(O(n*log(n))\)。该函数采用分治法，一旦找到每棵树的根节点，就会匹配这两棵树，并返回一个节点匹配列表。

因此，让我们用它来检查一个有 \(2^4 - 1\) 个节点的 2 元树是否是一个高度为 3 的平衡二叉树。

t1 = nx.balanced_tree(2, 3)
t2 = nx.full_rary_tree(2, 15)

from networkx.algorithms import isomorphism as iso

print("节点匹配")
iso.tree_isomorphism(t1, t2)

节点匹配

[(0, 0),
 (1, 1),
 (3, 3),
 (7, 7),
 (8, 8),
 (4, 4),
 (9, 9),
 (10, 10),
 (2, 2),
 (5, 5),
 (11, 11),
 (12, 12),
 (6, 6),
 (13, 13),
 (14, 14)]

高级算法#

VF2#

该算法用于解决图同构和子图同构问题。

VF2 是一种递归算法，在每一步中，我们将当前匹配函数扩展到覆盖更多节点，直到没有更多节点需要匹配。这不是一种暴力搜索方法，因为有一些可行性规则可以避免探索整个递归树。

形式上，我们有一个函数 \( M: s \rightarrow N(G) \times N(H) \)。\(M\) 是当前状态 \(s\) 下 \(G\) 和 \(H\) 节点子集之间的匹配函数。我们从初始状态 \(s_0\) 开始，\(M(s_0) = \emptyset\)。在每一步中，我们考虑一组节点，将当前状态 \(s\) 扩展到下一个状态 \(s'\)。在这个新状态下，\(M(s') = M(s) \cup {(g, h)} , g\in N(G), h\in N(H)\)。一致性条件是与 \(M(s)\) 相关的部分图 \(G\) 和 \(H\) 是同构的。有两种类型的可行性检查：

句法（图结构）：包括检查一致性条件和 k-前瞻规则，用于提前检查一个一致状态 \(s\) 在 k 步后是否有无一致后继状态。
语义（属性）。

伪代码：

Match(s):

输入：中间状态

输出：两个图之间的映射

IF M(s) 覆盖了 H 的所有节点 THEN:
    RETURN M(s)
ELSE:
    计算 P = {(g, h)...}，即要包含在 M(s) 中的候选节点集。
    FOR 每个 p in P:
        IF 包含 p 到 M(s) 的可行性规则成功 THEN:
            计算状态 s'
            MATCH(s')
       ENDIF
   ENDFOR
   恢复数据结构
ENDIF

让我们使用 VF2 来检查前一个示例中的图：

G = nx.path_graph(5)
G.add_edge(2, 5)

H = nx.path_graph(5)
H.add_edge(3, 5)

nx.is_isomorphic(G, H)

False

时间复杂度

最佳情况 \(\in \theta(n²)\)，如果只探索 \(n\) 个状态，例如每个节点只探索一次。
最坏情况 \(\in \theta(n!n)\)，如果必须完全探索所有可能的匹配。

同构 - 如何判断两个图是否相似？

Contents