弹性约束

一个约束 \(C(x) = c\) （等式可以替换为 \(\le\) 或 \(\ge\)）可以弹性化为以下形式

\[C(x) ∈ D\]

其中 \(D\) 表示包含值 \(c\) 的某个区间。

定义约束分两步进行：

1. 使用目标 \(c\) 实例化约束（LpConstraint 的子类）。

2. 调用它的 makeElasticSubProblem() 方法，该方法返回一个类型为 FixedElasticSubProblem 的对象（LpProblem 的子类）——其目标是使 \(C(x)\) 与 \(D\) 之间的距离最小化。

constraint = LpConstraint(..., rhs = c)
elasticProblem = constraint.makeElasticSubProblem(
                       penalty = <penalty_value>,
                       proportionFreeBound = <freebound_value>,
                       proportionFreeBoundList = <freebound_list_value>,
                       )

哪里：

• <penalty_value> 是一个实数

• <freebound_value> \(a \in [0,1]\) 指定了一个关于 \(c\) 的对称目标区间 \(D = (c(1-a),c(1+a))\)

• <freebound_list_value> = [a,b]，一个比例列表 \(a, b \in [0,1]\)，指定关于 \(c\) 的不对称目标区间 \(D = (c(1-a),c(1+b))\)

惩罚适用于约束在点 \(x\) 处，其中 \(C(x) \not \in D\)。<penalty_value> 的大小可以通过检查由 LpProblem.writeLP() 写入的 .lp 文件中的最终目标函数来评估。

示例：

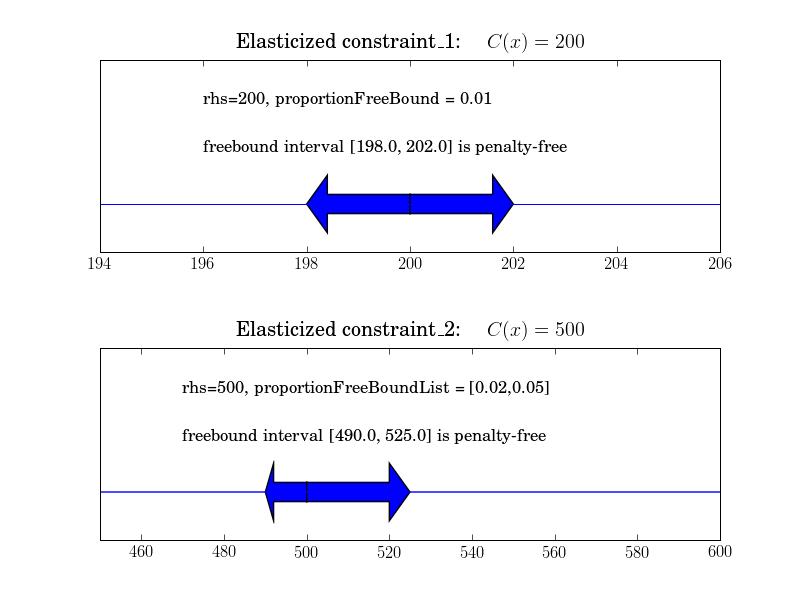
>>> constraint_1 = LpConstraint('ex_1',sense=1,rhs=200)
>>> elasticProblem_1 = constraint_1.makeElasticSubproblem(penalty=1, proportionFreeBound = 0.01)
>>> constraint_2 = LpConstraint('ex_2',sense=0,rhs=500)
>>> elasticProblem_2 = constraint_2.makeElasticSubproblem(penalty=1,
proportionFreeBoundList = [0.02, 0.05])

1. constraint_1 在 rhs 值的 1% 范围内有一个无惩罚的目标区间，即 200

2. constraint_2 在 rhs 值的左侧有 -2% 的免罚区间，右侧有 5% 的免罚区间，rhs 值为 500

以下是返回值的方法：