优化过程

解决优化问题不是一个线性过程，但这个过程可以分解为五个一般步骤：

获取问题描述
制定数学规划
解决数学规划问题
进行一些后优化分析
展示解决方案和分析

然而，在这个过程中经常存在“反馈循环”。例如，在制定并解决一个优化问题后，你通常会想要考虑你的解决方案的有效性（通常会与提供问题描述的人进行咨询）。如果你的解决方案无效，你可能需要修改或更新你的公式，以纳入你对实际问题的新理解。这一过程在运筹学方法论图中有所展示。

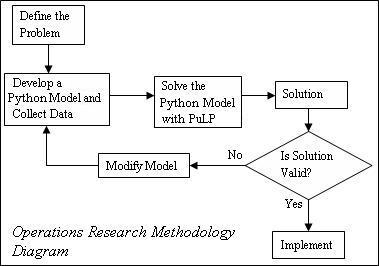
建模过程始于一个定义明确的模型描述，然后使用数学来制定一个数学程序。接下来，建模者将数学程序输入到某些求解器软件中，例如Excel，并求解模型。最后，解决方案根据原始模型描述转化为决策。

使用Python可以让你在建模过程中获得一个“捷径”。通过在Python中制定数学程序，你已经将其转换为一种可以被PuLP建模器轻松使用的形式，以便调用多种求解器，例如CPLEX、COIN、gurobi，因此你不需要将数学程序输入到求解器软件中。然而，你通常不会在公式中放入任何“硬”数字，而是使用数据文件来“填充”你的模型，因此在创建适当的数据文件时需要做一些工作。使用数据文件的优势在于，相同的模型可以多次使用不同的数据集。

建模过程

建模过程是对优化过程的“整洁有序”的简化。让我们更详细地考虑优化过程的五个步骤：

获取问题描述

这一步的目的是提出一个正式、严谨的模型描述。通常，你从一个问题的抽象描述和一些数据开始一个优化项目。通常你需要花一些时间和提供问题的人（通常称为客户）交谈。通过与客户交谈并考虑可用数据，你可以提出你习惯的更严谨的模型描述。有时并非所有数据都相关，或者你可能需要询问客户是否可以提供其他数据。有时可用数据的限制可能会显著改变你的模型描述和随后的公式。

制定数学规划

在这一步中，我们从问题描述中识别出关键的可量化决策、限制和目标，并在一个数学模型中捕捉它们的相互依赖关系。我们可以将公式化过程分解为4个关键步骤：

确定决策变量，特别注意单位（例如：我们需要决定每个流程每周运行多少小时）。
使用决策变量来构建目标函数，我们可以构造一个最小化或最大化的目标函数。目标函数通常反映了在给定决策变量值下的总成本或总利润。
制定约束条件，可以是逻辑上的（例如，我们不能为负数小时工作），或者是问题描述中明确指出的。同样，约束条件是用决策变量表示的。
确定目标函数和约束条件所需的数据。要解决您的数学规划问题，您需要有一些“硬数据”作为变量的边界和/或目标函数和/或约束条件中的变量系数。

解决数学规划问题

对于相对简单或已被充分理解的问题，数学模型通常可以被优化求解（即，找到最佳可能的解决方案）。这是通过使用诸如修正单纯形法或内点法等算法完成的。然而，许多工业问题使用这些技术求解到最优解所需的时间过长，因此使用不保证最优解的启发式方法来求解。

进行一些后优化分析

通常，问题描述中存在不确定性（无论是数据提供的准确性，还是未来数据值的不确定性）。在这种情况下，可以通过执行后优化分析来检验我们解决方案的鲁棒性。这涉及识别在各种变化下最优解如何变化（例如，给定成本增加或特定机器故障的影响是什么？）。这种分析对于制定战术或战略决策也很有用（例如，如果我们投资开设另一家工厂，这对我们的收入会有什么影响？）。

在这一步（以及下一步）中另一个重要的考虑是数学程序解决方案的验证。你应该仔细考虑解决方案的变量值在原始问题描述中的含义。确保它们对你和你的客户（这就是为什么下一步，展示解决方案和分析是重要的）都有意义。

展示解决方案和分析

优化过程中的一个关键步骤是解决方案的呈现和任何后优化分析。将数学程序的解决方案转化为简洁易懂的总结，与将问题描述转化为数学程序同样重要。通过优化生成的关键观察和决策必须以易于理解的方式呈现给客户或项目利益相关者。

你的演示是实施由你的数学程序生成的决策的关键第一步。如果决策及其后果（通常由数学程序的约束决定）没有被清晰和智能地展示，你的最优决策将永远不会被使用。

这一步也是你提出未来其他工作的机会。这可能包括：

定期监控您的数学程序的有效性；
进一步分析您的解决方案，寻找其他对您客户的好处；
识别未来的优化机会。