scipy.signal.windows.

chebwin

scipy.signal.windows.chebwin(M, at, sym=True)

返回一个 Dolph-Chebyshev 窗口。

参数:

M整数

输出窗口中的点数。如果为零，则返回一个空数组。如果为负数，则会抛出异常。

在浮动

衰减（以dB为单位）。

symbool, 可选

当为 True 时（默认），生成一个对称的窗口，用于滤波器设计。当为 False 时，生成一个周期性窗口，用于频谱分析。

返回:

wndarray

窗口，其最大值始终归一化为1

注释

此窗口针对给定阶数 M 和旁瓣等波纹衰减 at 的最窄主瓣宽度进行了优化，使用了切比雪夫多项式。它最初由 Dolph 开发，用于优化无线电天线阵列的方向性。

与大多数窗口不同，Dolph-Chebyshev 是根据其频率响应定义的：

\[W(k) = \frac {\cos\{M \cos^{-1}[\beta \cos(\frac{\pi k}{M})]\}} {\cosh[M \cosh^{-1}(\beta)]}\]

哪里

\[\beta = \cosh \left [\frac{1}{M} \cosh^{-1}(10^\frac{A}{20}) \right ]\]

并且 0 <= abs(k) <= M-1。A 是以分贝为单位的衰减 (at)。

然后使用 IFFT 生成时域窗口，因此 2 的幂 M 生成速度最快，而质数 M 生成速度最慢。

频域中的等波纹条件在时域中产生脉冲，这些脉冲出现在窗口的末端。

参考文献

[1]

C. Dolph, “A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level”, Proceedings of the IEEE, Vol. 34, Issue 6

[2]

Peter Lynch, “The Dolph-Chebyshev Window: A Simple Optimal Filter”, American Meteorological Society (April 1997) http://mathsci.ucd.ie/~plynch/Publications/Dolph.pdf

[3]

F. J. Harris, “On the use of windows for harmonic analysis with the discrete Fourier transforms”, Proceedings of the IEEE, Vol. 66, No. 1, January 1978

示例

Try it in your browser!

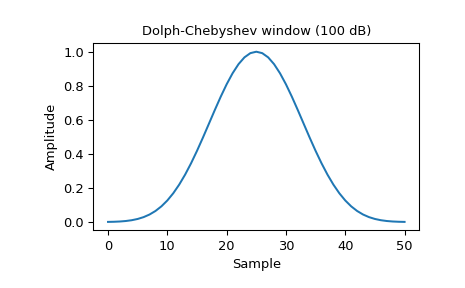
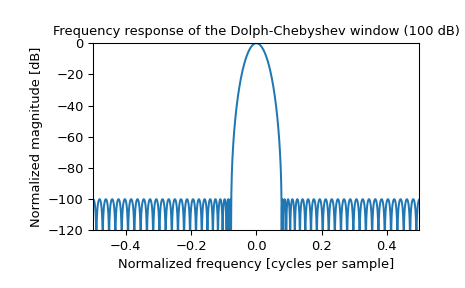
绘制窗口及其频率响应：

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = signal.windows.chebwin(51, at=100)
>>> plt.plot(window)
>>> plt.title("Dolph-Chebyshev window (100 dB)")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Dolph-Chebyshev window (100 dB)")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

Go BackOpen In Tab