scipy.signal.windows.

general_cosine

scipy.signal.windows.general_cosine(M, a, sym=True)

通用余弦项加权和窗口

参数:

M整数

输出窗口中的点数

aarray_like

权重系数的序列。这使用了以原点为中心的惯例，因此这些通常都是正数，而不是交替符号。

symbool, 可选

当为 True 时（默认），生成一个对称的窗口，用于滤波器设计。当为 False 时，生成一个周期性窗口，用于频谱分析。

返回:

wndarray

窗口值的数组。

参考文献

[1]

A. Nuttall, “Some windows with very good sidelobe behavior,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 29, no. 1, pp. 84-91, Feb 1981. DOI:10.1109/TASSP.1981.1163506.

[2]

Heinzel G. 等人，“通过离散傅里叶变换（DFT）进行频谱和频谱密度估计，包括全面的窗口函数列表和一些新的平顶窗口”，2002年2月15日，https://holometer.fnal.gov/GH_FFT.pdf

示例

Try it in your browser!

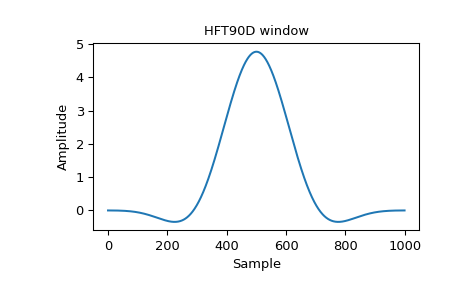
Heinzel 描述了一个名为“HFT90D”的平顶窗，其公式为：[2]

\[ \begin{align}\begin{aligned}w_j = 1 - 1.942604 \cos(z) + 1.340318 \cos(2z) - 0.440811 \cos(3z) + 0.043097 \cos(4z)\\w_j = 1 - 1.942604 \cos(z) + 1.340318 \cos(2z) - 0.440811 \cos(3z) + 0.043097 \cos(4z)\end{aligned}\end{align} \]

哪里

\[z = \frac{2 \pi j}{N}, j = 0...N - 1\]

由于这使用了从原点开始的惯例，为了重现窗口，我们需要将其他所有系数转换为正数：

>>> HFT90D = [1, 1.942604, 1.340318, 0.440811, 0.043097]

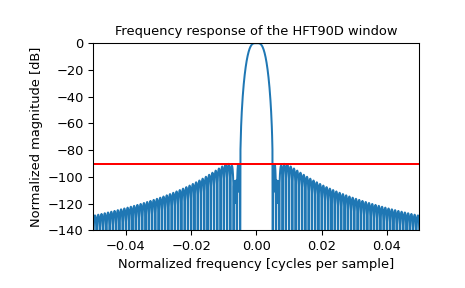
论文指出，最高的旁瓣位于-90.2 dB。通过绘制窗口及其频率响应来重现图42，并用红色确认旁瓣水平：

>>> import numpy as np
>>> from scipy.signal.windows import general_cosine
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = general_cosine(1000, HFT90D, sym=False)
>>> plt.plot(window)
>>> plt.title("HFT90D window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

>>> plt.figure()
>>> A = fft(window, 10000) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = np.abs(fftshift(A / abs(A).max()))
>>> response = 20 * np.log10(np.maximum(response, 1e-10))
>>> plt.plot(freq, response)
>>> plt.axis([-50/1000, 50/1000, -140, 0])
>>> plt.title("Frequency response of the HFT90D window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")
>>> plt.axhline(-90.2, color='red')
>>> plt.show()

Go BackOpen In Tab