scipy.signal.windows.

凯撒

scipy.signal.windows.kaiser(M, beta, sym=True)

返回一个 Kaiser 窗口。

Kaiser窗口是一种由使用贝塞尔函数形成的锥形。

参数:

M整数

输出窗口中的点数。如果为零，则返回一个空数组。如果为负数，则会抛出异常。

beta浮动

形状参数，决定主瓣宽度和旁瓣电平之间的权衡。随着 beta 变大，窗口变窄。

symbool, 可选

当为 True 时（默认），生成一个对称的窗口，用于滤波器设计。当为 False 时，生成一个周期性窗口，用于频谱分析。

返回:

wndarray

窗口，最大值归一化为1（但如果 M 是偶数且 sym 为 True，则值1不会出现）。

注释

Kaiser 窗口定义为

\[w(n) = I_0\left( \beta \sqrt{1-\frac{4n^2}{(M-1)^2}} \right)/I_0(\beta)\]

与

\[\quad -\frac{M-1}{2} \leq n \leq \frac{M-1}{2},\]

其中 \(I_0\) 是修正的零阶贝塞尔函数。

Kaiser 是以 Jim Kaiser 的名字命名的，他基于贝塞尔函数发现了一个简单的 DPSS 窗口近似。Kaiser 窗口是对数字长椭球序列（或 Slepian 窗口）的一个非常好的近似，这是相对于总能量最大化窗口主瓣能量的变换。

通过改变 beta 参数，Kaiser 可以近似其他窗口。（一些文献使用 alpha = beta/pi。） [4]

beta	窗口形状
0	矩形
5	类似于汉明码
6	类似于一个 Hann
8.6	类似于布莱克曼

β值为14可能是一个不错的起点。注意，随着β值变大，窗口会变窄，因此所需的样本数量需要足够大以采样越来越窄的尖峰，否则将返回NaN。

大多数对Kaiser窗口的引用来自信号处理文献，其中它被用作许多窗口函数之一来平滑数值。它也被称为消隐（这意味着“去除底部”，即平滑采样信号开始和结束处的间断）或锥形函数。

参考文献

[1]

J. F. Kaiser, “Digital Filters” - Ch 7 in “Systems analysis by digital computer”, Editors: F.F. Kuo and J.F. Kaiser, p 218-285. John Wiley and Sons, New York, (1966).

[2]

E.R. Kanasewich, 《地球物理学中的时间序列分析》，阿尔伯塔大学出版社，1975年，第177-178页。

[3]

维基百科，“窗口函数”，https://en.wikipedia.org/wiki/Window_function

[4]

F. J. Harris, “On the use of windows for harmonic analysis with the discrete Fourier transform,” Proceedings of the IEEE, vol. 66, no. 1, pp. 51-83, Jan. 1978. DOI:10.1109/PROC.1978.10837.

示例

Try it in your browser!

绘制窗口及其频率响应：

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

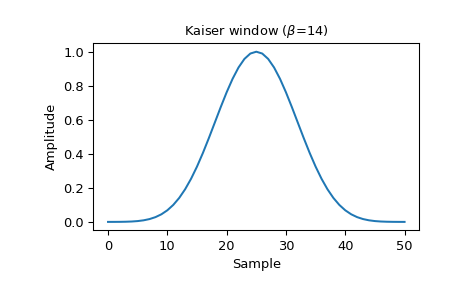
>>> window = signal.windows.kaiser(51, beta=14)
>>> plt.plot(window)
>>> plt.title(r"Kaiser window ($\beta$=14)")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

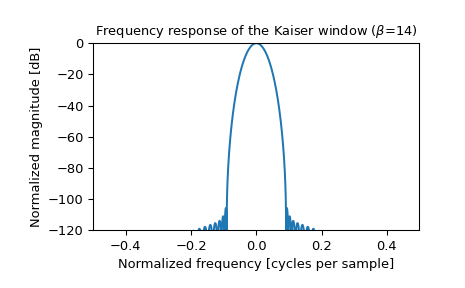
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title(r"Frequency response of the Kaiser window ($\beta$=14)")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

Go BackOpen In Tab