scipy.signal.windows.

lanczos

scipy.signal.windows.lanczos(M, *, sym=True)

返回一个Lanczos窗口，也称为sinc窗口。

参数:

M整数

输出窗口中的点数。如果为零，则返回一个空数组。如果为负数，则会抛出异常。

symbool, 可选

当为 True 时（默认），生成一个对称的窗口，用于滤波器设计。当为 False 时，生成一个周期性窗口，用于频谱分析。

返回:

wndarray

窗口，最大值归一化为1（但如果 M 是偶数且 sym 为 True，则值1不会出现）。

注释

Lanczos 窗口定义为

\[w(n) = sinc \left( \frac{2n}{M - 1} - 1 \right)\]

哪里

\[sinc(x) = \frac{\sin(\pi x)}{\pi x}\]

Lanczos 窗口减少了 Gibbs 振荡，并广泛用于具有良好物理和频谱域特性的气候时间序列滤波。

Added in version 1.10.

参考文献

[1]

Lanczos, C., 和 Teichmann, T. (1957). 应用分析。物理今日, 10, 44.

[2]

Duchon C. E. (1979) 在一维和二维中的Lanczos滤波。应用气象学杂志，第18卷，第1016-1022页。

[3]

Thomson, R. E. 和 Emery, W. J. (2014) 《物理海洋学数据分析方法》（第三版），Elsevier，第593-637页。

[4]

Wikipedia, “窗口函数”, http://en.wikipedia.org/wiki/Window_function

示例

Try it in your browser!

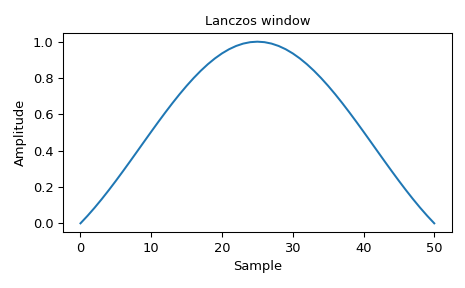
绘制窗口

>>> import numpy as np
>>> from scipy.signal.windows import lanczos
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1)
>>> window = lanczos(51)
>>> ax.plot(window)
>>> ax.set_title("Lanczos window")
>>> ax.set_ylabel("Amplitude")
>>> ax.set_xlabel("Sample")
>>> fig.tight_layout()
>>> plt.show()

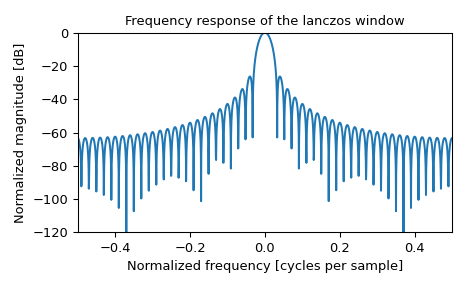
及其频率响应：

>>> fig, ax = plt.subplots(1)
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> ax.plot(freq, response)
>>> ax.set_xlim(-0.5, 0.5)
>>> ax.set_ylim(-120, 0)
>>> ax.set_title("Frequency response of the lanczos window")
>>> ax.set_ylabel("Normalized magnitude [dB]")
>>> ax.set_xlabel("Normalized frequency [cycles per sample]")
>>> fig.tight_layout()
>>> plt.show()

Go BackOpen In Tab