scipy.spatial.transform.

RotationSpline

class scipy.spatial.transform.RotationSpline(times, rotations)

使用连续的角速度和加速度进行旋转插值。

每个连续方向之间的旋转矢量是时间的立方函数，并且保证角速度和加速度是连续的。这种插值类似于三次样条插值。

关于数学和实现细节，请参阅 [1]。

参数:

时间array_like, 形状 (N,)

已知旋转的次数。至少必须指定2次。

旋转 : 旋转 实例旋转实例

要执行插值的旋转。必须包含 N 个旋转。

方法

__call__(times[, order])

计算插值后的值。

参考文献

[1]

平滑姿态插值

示例

Try it in your browser!

>>> from scipy.spatial.transform import Rotation, RotationSpline
>>> import numpy as np

定义从欧拉角得出的时间和旋转序列：

>>> times = [0, 10, 20, 40]
>>> angles = [[-10, 20, 30], [0, 15, 40], [-30, 45, 30], [20, 45, 90]]
>>> rotations = Rotation.from_euler('XYZ', angles, degrees=True)

创建插值器对象：

>>> spline = RotationSpline(times, rotations)

插值欧拉角、角速度和角加速度：

>>> angular_rate = np.rad2deg(spline(times, 1))
>>> angular_acceleration = np.rad2deg(spline(times, 2))
>>> times_plot = np.linspace(times[0], times[-1], 100)
>>> angles_plot = spline(times_plot).as_euler('XYZ', degrees=True)
>>> angular_rate_plot = np.rad2deg(spline(times_plot, 1))
>>> angular_acceleration_plot = np.rad2deg(spline(times_plot, 2))

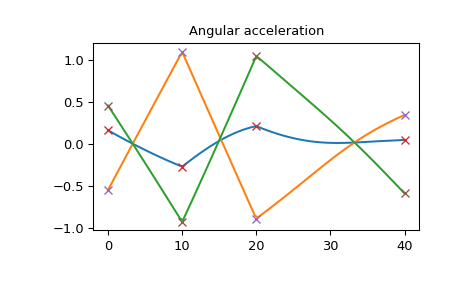
在这张图中，你可以看到欧拉角是连续且平滑的：

>>> import matplotlib.pyplot as plt
>>> plt.plot(times_plot, angles_plot)
>>> plt.plot(times, angles, 'x')
>>> plt.title("Euler angles")
>>> plt.show()

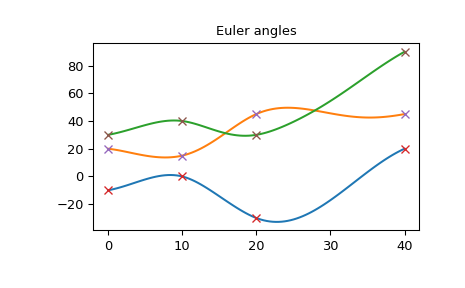
角速度也很平稳：

>>> plt.plot(times_plot, angular_rate_plot)
>>> plt.plot(times, angular_rate, 'x')
>>> plt.title("Angular rate")
>>> plt.show()

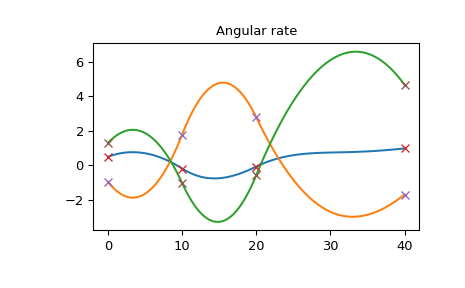
角加速度是连续的，但不是平滑的。还要注意，角加速度不是分段线性函数，因为它与旋转矢量的二阶导数（在三次样条中是分段线性函数）不同。

>>> plt.plot(times_plot, angular_acceleration_plot)
>>> plt.plot(times, angular_acceleration, 'x')
>>> plt.title("Angular acceleration")
>>> plt.show()

Go BackOpen In Tab