解释公平性的定量衡量

这篇实践性文章将可解释AI方法与公平性度量联系起来，并展示了现代可解释性方法如何增强定量公平性度量的实用性。通过使用 `SHAP <http://github.com/shap/shap>`__（一个流行的可解释AI工具），我们可以分解公平性度量，并为模型输入特征之间的任何观察到的差异分配责任。解释这些定量公平性度量可以减少依赖它们作为不透明公平性标准的倾向，并促进将其作为理解模型在不同群体间行为差异的工具的明智使用。

定量公平性指标试图将数学精确性引入机器学习中公平性的定义 [1]。然而，公平性的定义深深植根于人类的伦理原则，因此依赖于通常在机器学习模型使用情境中至关重要的价值判断。这种对价值判断的实际依赖在定量公平性度量的数学中表现为一组在某些情况下相互不兼容的公平性定义之间的权衡 [2]。由于公平性依赖于情境相关的价值判断，将定量公平性指标视为公平性的不透明黑箱度量是危险的，因为这样做可能会掩盖重要的价值判断选择。

如何使用 SHAP 解释模型的各种公平性指标

本文不是关于如何选择“正确”的模型公平性度量，而是关于解释你选择的任何度量。哪种公平性度量最合适取决于你的具体情境，例如适用的法律、机器学习模型输出对人们的影响，以及你对各种结果及其权衡的重视程度。这里我们将使用经典的 demographic parity 度量，因为它简单且与法律上的差别影响概念紧密相关。同样的分析也可以应用于其他度量，如 决策理论成本、同等机会、同等质量服务 等。人口统计学平权指出，机器学习模型的输出在两个或多个群体之间应该是相等的。人口统计学平权差异则是衡量模型在两个样本群体中结果差异的度量。

由于SHAP将模型输出分解为与原始模型输出单位相同的特征归属，我们可以首先使用SHAP将模型输出分解到每个输入特征中，然后使用该特征的SHAP值分别计算每个输入特征的群体公平性差异（或其他任何公平性指标）。 因为SHAP值的总和等于模型的输出，所以SHAP值的群体公平性差异的总和也等于整个模型的群体公平性差异。

SHAP 公平性解释在各种模拟场景中的表现

为了帮助我们探索解释量化公平性指标的潜在有用性，我们考虑了一个基于信用承保的简单模拟场景。在我们的模拟中，有四个潜在因素驱动贷款违约的风险：收入稳定性、收入金额、支出克制和一致性。这些潜在因素是不可观察的，但它们各自影响四个不同的可观察特征：工作历史、报告的收入、信用查询和逾期付款。使用这个模拟，我们生成随机样本，然后训练一个非线性的 XGBoost 分类器来预测违约概率。同样的过程也适用于SHAP支持的任何其他模型类型，只需记住，更复杂模型的解释会隐藏更多模型的细节。

通过在完全指定的模拟中引入性别特定的报告错误，我们可以观察到这些错误导致的偏见如何被我们选择的公平性指标捕捉到。在我们的模拟案例中，真实标签（贷款违约）在统计上与性别（我们用来检查公平性的敏感类别）无关。因此，男女之间的任何差异意味着一个或两个群体由于特征测量错误、标签错误或模型错误而被错误地建模。如果你预测的真实标签（可能与你可访问的训练标签不同）在统计上与你在考虑的敏感特征不独立，那么即使是一个没有错误的完美模型也会在人口统计平等方面失败。在这些情况下，公平性解释可以帮助你确定哪些人口统计差异的来源是有效的。

# here we define a function that we can call to execute our simulation under
# a variety of different alternative scenarios
import numpy as np
import pandas as pd

import shap

%config InlineBackend.figure_format = 'retina'


def run_credit_experiment(
    N,
    job_history_sex_impact=0,
    reported_income_sex_impact=0,
    income_sex_impact=0,
    late_payments_sex_impact=0,
    default_rate_sex_impact=0,
    include_brandx_purchase_score=False,
    include_sex=False,
):
    np.random.seed(0)
    sex = np.random.randint(0, 2, N) == 1  # randomly half men and half women

    # four hypothetical causal factors influence customer quality
    # they are all scaled to the same units between 0-1
    income_stability = np.random.rand(N)
    income_amount = np.random.rand(N)
    if income_sex_impact > 0:
        income_amount -= income_sex_impact / 90000 * sex * np.random.rand(N)
        income_amount -= income_amount.min()
        income_amount /= income_amount.max()
    spending_restraint = np.random.rand(N)
    consistency = np.random.rand(N)

    # intuitively this product says that high customer quality comes from simultaneously
    # being strong in all factors
    customer_quality = (
        income_stability * income_amount * spending_restraint * consistency
    )

    # job history is a random function of the underlying income stability feature
    job_history = np.maximum(
        10 * income_stability
        + 2 * np.random.rand(N)
        - job_history_sex_impact * sex * np.random.rand(N),
        0,
    )

    # reported income is a random function of the underlying income amount feature
    reported_income = np.maximum(
        10000
        + 90000 * income_amount
        + np.random.randn(N) * 10000
        - reported_income_sex_impact * sex * np.random.rand(N),
        0,
    )

    # credit inquiries is a random function of the underlying spending restraint and income amount features
    credit_inquiries = np.round(
        6 * np.maximum(-spending_restraint + income_amount, 0)
    ) + np.round(np.random.rand(N) > 0.1)

    # credit inquiries is a random function of the underlying consistency and income stability features
    late_payments = np.maximum(
        np.round(3 * np.maximum((1 - consistency) + 0.2 * (1 - income_stability), 0))
        + np.round(np.random.rand(N) > 0.1)
        - np.round(late_payments_sex_impact * sex * np.random.rand(N)),
        0,
    )

    # bundle everything into a data frame and define the labels based on the default rate and customer quality
    X = pd.DataFrame(
        {
            "Job history": job_history,
            "Reported income": reported_income,
            "Credit inquiries": credit_inquiries,
            "Late payments": late_payments,
        }
    )
    default_rate = 0.40 + sex * default_rate_sex_impact
    y = customer_quality < np.percentile(customer_quality, default_rate * 100)

    if include_brandx_purchase_score:
        brandx_purchase_score = sex + 0.8 * np.random.randn(N)
        X["Brand X purchase score"] = brandx_purchase_score

    if include_sex:
        X["Sex"] = sex + 0

    # build model
    import xgboost

    model = xgboost.XGBClassifier(
        max_depth=1, n_estimators=500, subsample=0.5, learning_rate=0.05
    )
    model.fit(X, y)

    # build explanation
    import shap

    explainer = shap.TreeExplainer(model, shap.sample(X, 100))
    shap_values = explainer.shap_values(X)

    return shap_values, sex, X, explainer.expected_value

场景A：无报告错误

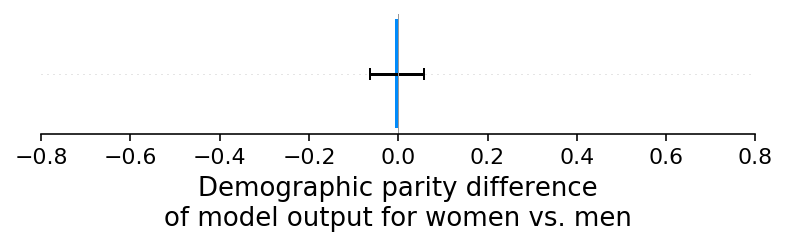
我们的第一个实验是一个简单的基线检查，我们避免引入任何性别特定的报告错误。虽然我们可以使用任何模型输出来衡量人口统计平价，但我们使用二元XGBoost分类器的连续对数几率分数。正如预期的那样，这个基线实验结果显示男性和女性的信用评分之间没有显著的人口统计平价差异。我们可以通过绘制女性和男性平均信用评分的差异作为条形图，并注意到零接近误差范围来看到这一点（注意，负值意味着女性的平均预测风险低于男性，而正值意味着女性的平均预测风险高于男性）：

N = 10000
shap_values_A, sex_A, X_A, ev_A = run_credit_experiment(N)
model_outputs_A = ev_A + shap_values_A.sum(1)
glabel = "Demographic parity difference\nof model output for women vs. men"
xmin = -0.8
xmax = 0.8
shap.group_difference_plot(
    shap_values_A.sum(1), sex_A, xmin=xmin, xmax=xmax, xlabel=glabel
)

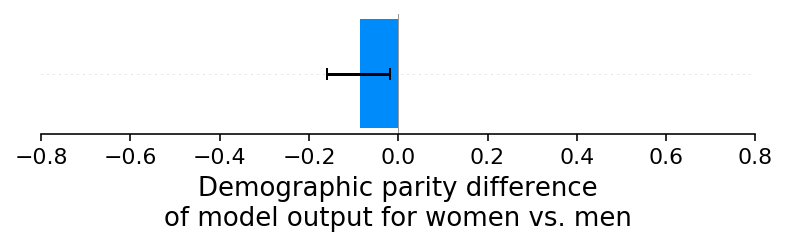
现在我们可以使用 SHAP 来分解模型输出在每个模型输入特征之间的分布，然后计算每个特征所归属的成分上的群体公平性差异。如上所述，由于 SHAP 值的总和等于模型的输出，因此每个特征的 SHAP 值的群体公平性差异的总和等于整个模型的群体公平性差异。这意味着下面条形图的总和等于上面的条形图（我们基线情景模型的群体公平性差异）。

slabel = "Demographic parity difference\nof SHAP values for women vs. men"
shap.group_difference_plot(
    shap_values_A, sex_A, X_A.columns, xmin=xmin, xmax=xmax, xlabel=slabel
)

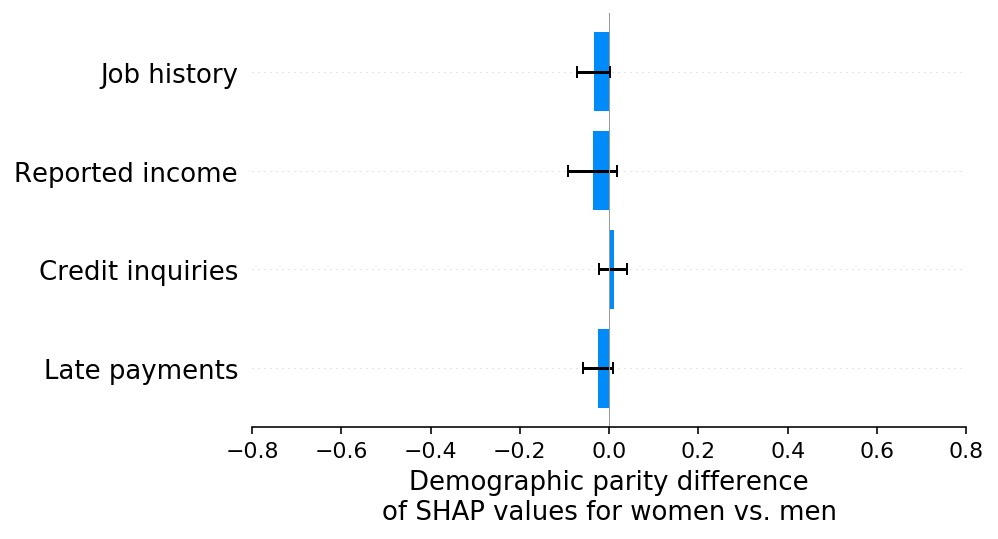
场景B：女性收入的少报偏差

在我们的基线场景中，我们设计了一个模拟，其中性别对模型使用的任何特征或标签都没有影响。在这里的场景B中，我们在模拟中引入了女性收入的少报偏差。这里的关键不是女性收入在现实世界中被少报的可能性有多大，而是我们如何识别出引入了性别特定的偏差，并理解其来源。通过绘制女性和男性之间平均模型输出（默认风险）的差异，我们可以看到收入少报偏差已经造成了显著的人口统计平价差异，现在女性的默认风险高于男性：

shap_values_B, sex_B, X_B, ev_B = run_credit_experiment(
    N, reported_income_sex_impact=30000
)
model_outputs_B = ev_B + shap_values_B.sum(1)
shap.group_difference_plot(
    shap_values_B.sum(1), sex_B, xmin=xmin, xmax=xmax, xlabel=glabel
)

 95%|=================== | 9542/10000 [00:11<00:00]

如果这是一个真实的应用，这种人口统计学上的差异可能会触发对模型的深入分析，以确定是什么导致了这种差异。虽然仅凭一个单一的人口统计学差异值进行调查是具有挑战性的，但基于SHAP的每个特征的人口统计学差异分解使得这一过程变得容易得多。使用SHAP，我们可以看到报告的收入特征存在显著的偏差，这使得女性的风险相对于男性不成比例地增加。这使我们能够快速识别出哪个特征的报告偏差导致了我们的模型违反了人口统计学上的公平性：

shap.group_difference_plot(
    shap_values_B, sex_B, X_B.columns, xmin=xmin, xmax=xmax, xlabel=slabel
)

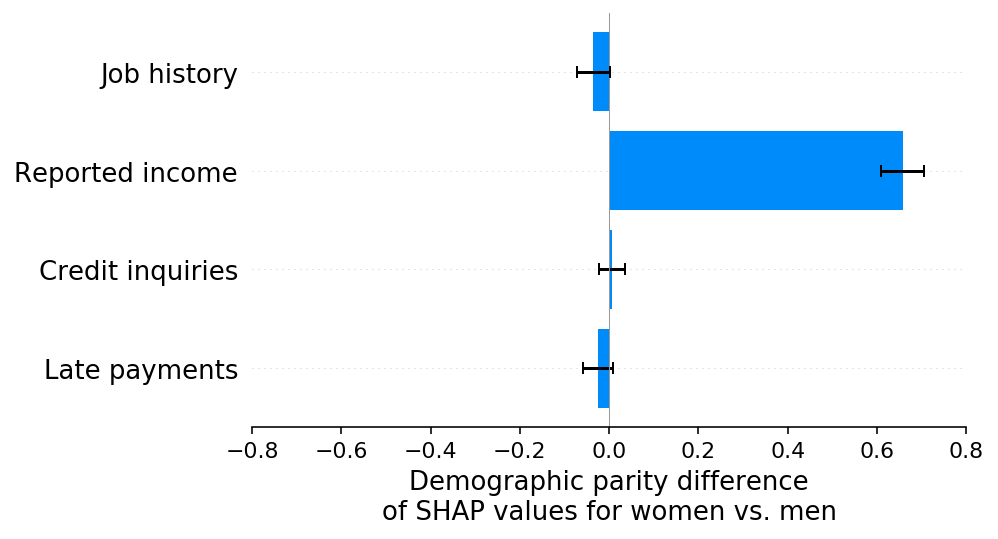
值得注意的是，在这一阶段，我们的假设如何影响SHAP公平性解释的解读。在我们的模拟场景中，我们知道女性的实际收入与男性相同，因此当我们看到报告的收入特征对女性的偏见低于男性时，我们知道这是由于报告收入特征中的测量误差偏见所致。解决这个问题的最佳方法是找出如何消除报告收入特征中的测量误差偏见。这样做将创建一个更准确的模型，同时减少人口统计学上的差异。然而，如果我们假设女性实际上比男性赚得更少（而不仅仅是报告错误），那么我们就不能仅仅“修复”报告的收入特征。相反，我们必须仔细考虑如何最好地解释两个受保护群体之间实际的违约风险差异。仅使用SHAP公平性解释无法确定这两种情况中的哪一种正在发生，因为在两种情况下，报告的收入特征都将导致预测的男性和女性风险之间的观察差异。

场景C：女性逾期还款的少报偏差

为了验证SHAP人口统计公平性解释能够正确检测到无论效果方向或来源特征的差异，我们重复了之前的实验，但这次不是对收入进行低报偏差，而是对女性的逾期付款率进行低报偏差。这导致模型的输出在人口统计公平性上出现了显著差异，现在女性的平均违约风险低于男性：

shap_values_C, sex_C, X_C, ev_C = run_credit_experiment(N, late_payments_sex_impact=2)
model_outputs_C = ev_C + shap_values_C.sum(1)
shap.group_difference_plot(
    shap_values_C.sum(1), sex_C, xmin=xmin, xmax=xmax, xlabel=glabel
)

正如我们所希望的，SHAP 解释正确地突出了延迟付款特征作为模型人口统计平价差异的原因，以及效果的方向：

shap.group_difference_plot(
    shap_values_C, sex_C, X_C.columns, xmin=xmin, xmax=xmax, xlabel=slabel
)

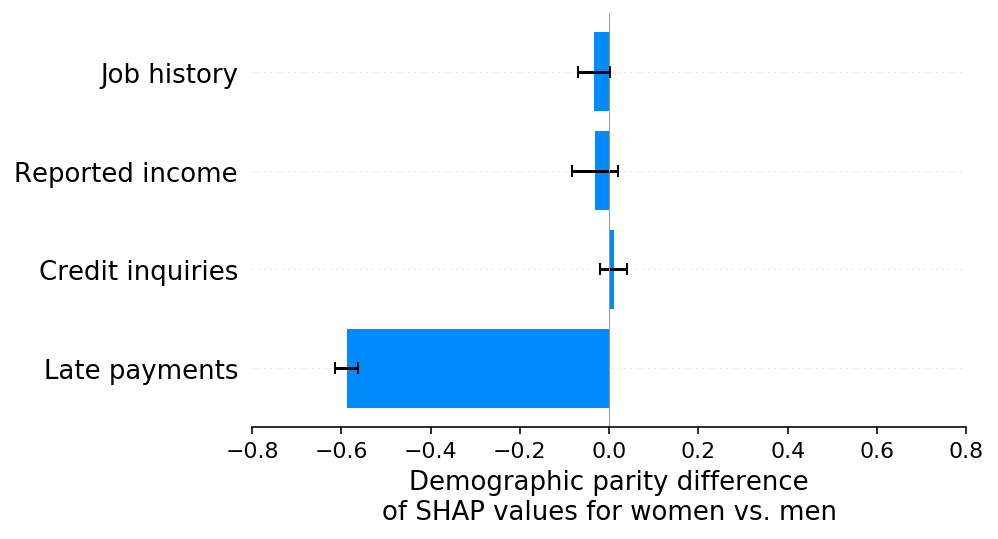
场景D：女性违约率的低报偏差

上述实验主要集中在介绍特定输入特征的报告错误。接下来我们考虑当我们通过女性违约率的低报偏差（这意味着女性的违约不太可能被报告）在训练标签上引入报告错误时会发生什么。有趣的是，对于我们模拟的情景，这导致模型输出中没有显著的人口统计平价差异：

shap_values_D, sex_D, X_D, ev_D = run_credit_experiment(
    N, default_rate_sex_impact=-0.1
)  # 20% change
model_outputs_D = ev_D + shap_values_D.sum(1)
shap.group_difference_plot(
    shap_values_D.sum(1), sex_D, xmin=xmin, xmax=xmax, xlabel=glabel
)

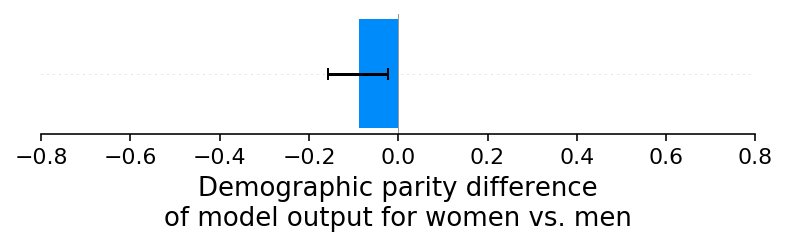
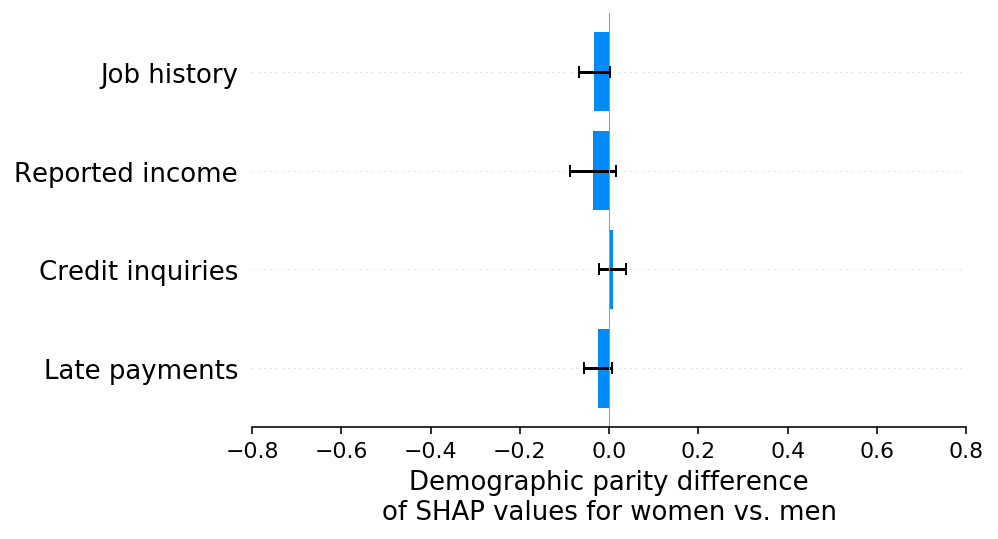
我们也没有在SHAP解释中看到任何人口统计学平等方面差异的证据：

shap.group_difference_plot(
    shap_values_D, sex_D, X_D.columns, xmin=xmin, xmax=xmax, xlabel=slabel
)

场景E：女性违约率的低报偏差，第二部分

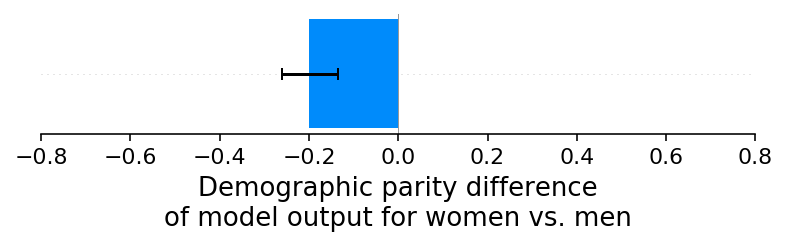
最初可能会令人惊讶的是，当我们引入女性违约率的低报偏差时，并没有导致人口统计学上的公平性差异。这是因为我们的模拟中的四个特征与性别都没有显著的相关性，因此它们都无法有效地用于建模我们引入到训练标签中的偏差。如果我们现在改为向模型提供一个与性别相关的新特征（品牌X购买分数），那么我们会看到人口统计学上的公平性差异出现，因为这个特征被模型用来捕捉训练标签中的性别特定偏差：

shap_values_E, sex_E, X_E, ev_E = run_credit_experiment(
    N, default_rate_sex_impact=-0.1, include_brandx_purchase_score=True
)
model_outputs_E = ev_E + shap_values_E.sum(1)
shap.group_difference_plot(
    shap_values_E.sum(1), sex_E, xmin=xmin, xmax=xmax, xlabel=glabel
)

 98%|===================| 9794/10000 [00:11<00:00]

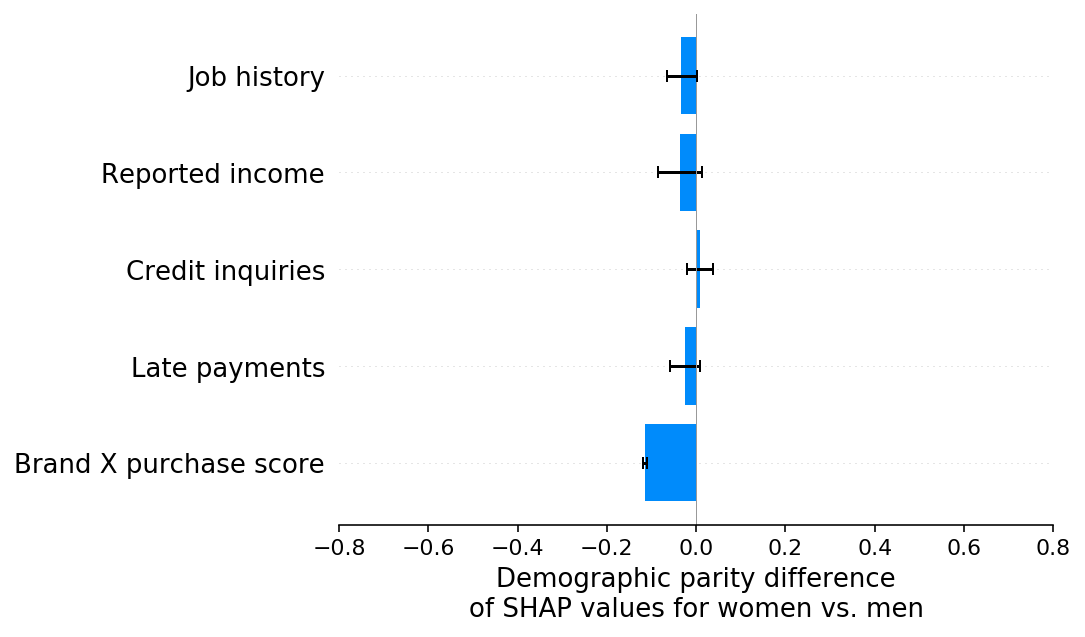
当我们用SHAP解释人口统计学平价差异时，我们可以看到，正如预期的那样，品牌X购买评分特征驱动了这种差异。在这种情况下，这并不是因为我们测量品牌X购买评分特征的方式存在偏见，而是因为我们的训练标签存在偏见，这种偏见被任何与性别有足够相关性的输入特征所捕捉到。

shap.group_difference_plot(
    shap_values_E, sex_E, X_E.columns, xmin=xmin, xmax=xmax, xlabel=slabel
)

场景 F：分解多个少报偏差

当存在单一的报告偏差时，模型输出的经典人口统计均等性测试和人口统计均等性测试的SHAP解释会捕捉到相同的偏差效应（尽管SHAP解释通常具有更高的统计显著性，因为它隔离了导致偏差的特征）。但是，当数据集中存在多种偏差时会发生什么？在这个实验中，我们引入了两种这样的偏差，即女性违约率的低报和女性工作历史的低报。这些偏差在全球平均水平上倾向于相互抵消，因此在模型输出的均等性测试中没有显示出可测量的差异：

shap_values_F, sex_F, X_F, ev_F = run_credit_experiment(
    N,
    default_rate_sex_impact=-0.1,
    include_brandx_purchase_score=True,
    job_history_sex_impact=2,
)
model_outputs_F = ev_F + shap_values_F.sum(1)
shap.group_difference_plot(
    shap_values_F.sum(1), sex_F, xmin=xmin, xmax=xmax, xlabel=glabel
)

100%|===================| 9996/10000 [00:11<00:00]

然而，如果我们查看人口统计学平权差异的SHAP解释，我们可以清楚地看到两种（相互抵消的）偏见：

shap.group_difference_plot(
    shap_values_F, sex_F, X_F.columns, xmin=xmin, xmax=xmax, xlabel=slabel
)

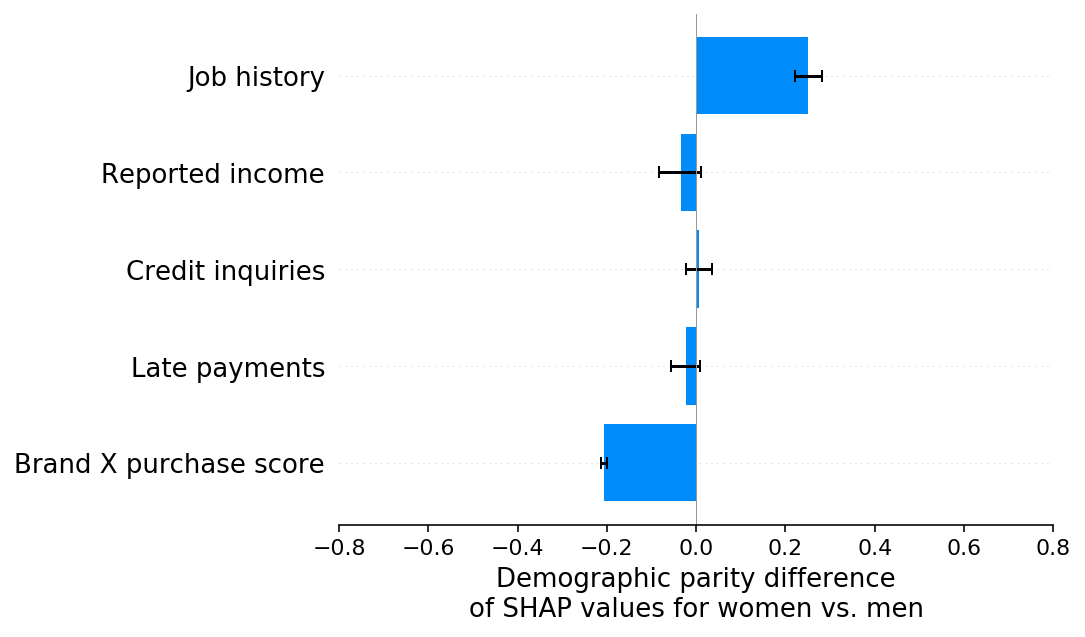
识别多个可能相互抵消的偏见效应可能很重要，因为尽管平均而言对男性或女性没有不同的影响，但对个人却有不同的影响。例如，在这个模拟中，没有在品牌X购物的女性将获得比应有分数更低的信用评分，这是由于工作历史报告中的偏见所致。

如何引入一个受保护的特征可以帮助区分标签偏差和特征偏差

在场景 F 中，我们能够分解出两种不同的偏见形式，一种来自工作历史报告不足，另一种来自违约率报告不足。然而，违约率报告不足的偏见并非归因于违约率标签，而是归因于与性别相关的品牌 X 购买评分特征。这仍然让我们对人口统计平价差异的真实来源存在一些不确定性，因为任何归因于输入特征的差异可能是由于该特征的问题，或者是由于训练标签的问题。

事实证明，在这种情况下，我们可以通过将性别直接引入模型来帮助区分标签偏差和特征偏差。引入性别作为输入特征的目的是使标签偏差完全落在性别特征上，而保持特征偏差不变。因此，我们可以通过比较上述场景F的结果与下面新场景G的结果来区分标签偏差和特征偏差。当然，这会创造出比之前更强的群体平等差异，但这没关系，因为我们的目标不是偏差缓解，而是偏差理解。

shap_values_G, sex_G, X_G, ev_G = run_credit_experiment(
    N,
    default_rate_sex_impact=-0.1,
    include_brandx_purchase_score=True,
    job_history_sex_impact=2,
    include_sex=True,
)
model_outputs_G = ev_G + shap_values_G.sum(1)
shap.group_difference_plot(
    shap_values_G.sum(1), sex_G, xmin=xmin, xmax=xmax, xlabel=glabel
)

 97%|=================== | 9720/10000 [00:11<00:00]

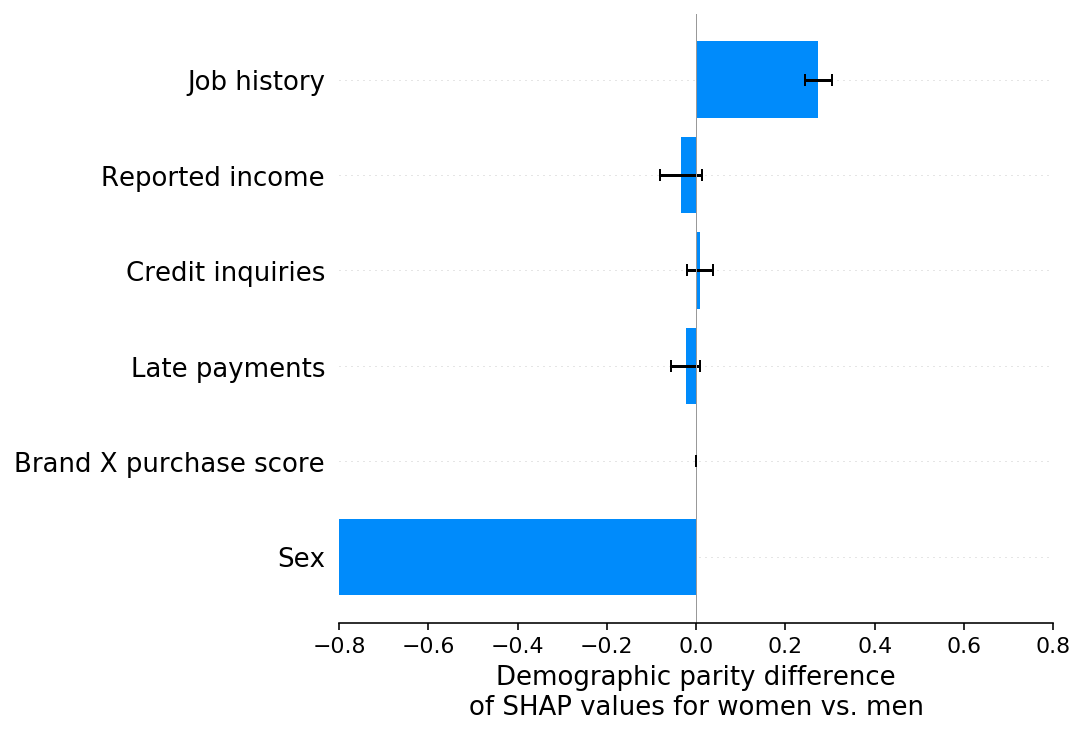
场景 G 的 SHAP 解释显示，原本在场景 F 中与品牌 X 购买评分特征相关的所有人口统计平价差异现在已转移到性别特征上，而原本在场景 F 中与工作历史特征相关的人口统计平价差异则没有移动。这可以解释为，场景 F 中归因于品牌 X 购买评分的所有差异是由于标签偏差，而场景 F 中归因于工作历史的所有差异是由于特征偏差。

shap.group_difference_plot(
    shap_values_G, sex_G, X_G.columns, xmin=xmin, xmax=xmax, xlabel=slabel
)

结论

公平性是一个复杂的主题，其中清晰的数学答案几乎总是伴随着注意事项，并依赖于伦理价值判断。这意味着，特别重要的是，不仅要将公平性指标作为黑箱使用，而是要寻求理解这些指标是如何计算的，以及你的模型和训练数据的哪些方面正在影响你观察到的任何差异。使用SHAP分解定量公平性指标可以减少这些指标的透明度，当这些指标受到仅影响少数特征的测量偏差驱动时。我希望你发现我们在这里展示的公平性解释能帮助你更好地应对公平性评估中固有的价值判断，从而帮助减少在现实世界情境中使用公平性指标时可能带来的意外后果的风险。