特性
这是LightGBM工作原理的概念性概述[1]。我们假设读者熟悉决策树提升算法,因此将重点放在LightGBM与其他提升包可能不同的方面。有关详细算法,请参阅参考文献或源代码。
速度和内存使用的优化
许多提升工具使用基于预排序的算法`[2, 3] <#references>`__(例如xgboost中的默认算法)进行决策树学习。这是一种简单的解决方案,但不容易优化。
LightGBM 使用基于直方图的算法 [4, 5, 6] ,将连续特征(属性)值分桶到离散的箱中。这加快了训练速度并减少了内存使用。基于直方图算法的优势包括以下几点:
减少计算每个分割增益的成本
基于预排序的算法具有时间复杂度
O(#data)计算直方图的时间复杂度为
O(#data),但这只涉及一个快速的求和操作。一旦直方图构建完成,基于直方图的算法的时间复杂度为O(#bins),而#bins远小于#data。
使用直方图减法以进一步加速
要在二叉树中获取一个叶子的直方图,可以使用其父节点和其邻居的直方图相减。
因此,它只需要为一个叶子(其
#data比其邻居小)构建直方图。然后,它可以通过直方图减法以较小的成本(O(#bins))获得其邻居的直方图。
减少内存使用
将连续值替换为离散的区间。如果
#bins较小,可以使用较小的数据类型(例如 uint8_t)来存储训练数据。无需为预排序功能值存储额外信息
减少分布式学习的通信成本
稀疏优化
仅需
O(2 * #非零数据)来构建稀疏特征的直方图
准确性优化
叶向(最佳优先)树生长
大多数决策树学习算法通过按层(深度)方式生长树,如下图像所示:
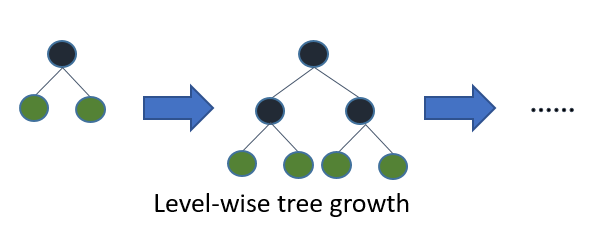
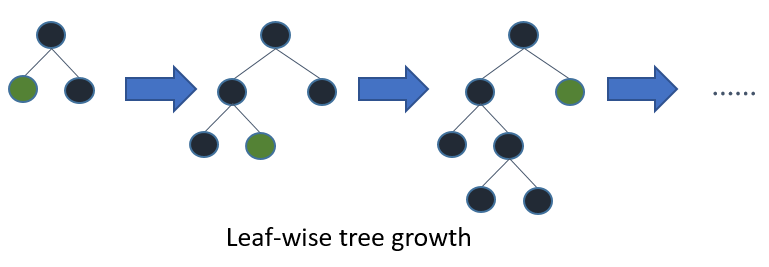
LightGBM 以叶向(最佳优先)方式生长树 [7]。它会选择具有最大 delta 损失的叶进行生长。在固定 #叶 的情况下,叶向算法往往比层向算法实现更低的损失。
当 #data 较小时,Leaf-wise 可能导致过拟合,因此 LightGBM 包含了 max_depth 参数来限制树的深度。然而,即使指定了 max_depth,树仍然以 Leaf-wise 方式生长。
分类特征的最佳分割
通常使用独热编码来表示分类特征,但对于树学习器来说,这种方法并不理想。特别是对于高基数的分类特征,基于独热特征构建的树往往不平衡,并且需要非常深才能达到良好的准确性。
与独热编码不同,最佳解决方案是通过将分类特征的类别划分为两个子集来进行分割。如果特征有 k 个类别,则有 2^(k-1) - 1 种可能的划分方式。但对于回归树,存在一种高效的解决方案[8]。它大约需要 O(k * log(k)) 来找到最优划分。
基本思想是根据每个分割点的训练目标对类别进行排序。更具体地说,LightGBM 根据其累积值(sum_gradient / sum_hessian)对直方图(对于分类特征)进行排序,然后在排序后的直方图上找到最佳分割点。
网络通信中的优化
在LightGBM的分布式学习中,只需使用一些集体通信算法,如“All reduce”、“All gather”和“Reduce scatter”。LightGBM实现了最先进的算法[9]。这些集体通信算法比点对点通信能提供更好的性能。
分布式学习中的优化
LightGBM 提供了以下分布式学习算法。
功能并行
传统算法
特征并行旨在并行化决策树中的“寻找最佳分割”。传统特征并行的过程是:
垂直分区数据(不同的机器拥有不同的特征集)。
工人在本地特征集上找到局部最佳分割点 {特征, 阈值}。
相互交流本地的最佳分割,并获取最佳的一个。
选择最佳分割的工作者进行分割,然后将分割后的数据结果发送给其他工作者。
其他工作人员根据接收到的数据分割数据。
传统特征并行的不足之处:
由于无法加速时间复杂度为
O(#data)的“分割”操作,因此存在计算开销。因此,当#data很大时,特征并行无法很好地加速。需要分割结果的通信,其成本约为 ``O(#data / 8)``(每个数据使用一位)。
LightGBM 中的特征并行
由于特征并行在 #data 较大时无法很好地加速,我们做了一些改变:每个工作节点不再垂直分区数据,而是持有完整的数据。因此,LightGBM 不需要为数据的分割结果进行通信,因为每个工作节点都知道如何分割数据。并且 #data 不会变得更大,所以在每台机器上持有完整数据是合理的。
LightGBM 中特征并行的过程:
工人在本地特征集上找到局部最佳分割点 {特征, 阈值}。
相互交流本地的最佳分割,并获取最佳的一个。
执行最佳分割。
然而,这个并行算法在 #data 很大时仍然存在“分割”计算开销的问题。因此,当 #data 很大时,使用数据并行会更好。
数据并行
传统算法
数据并行旨在并行化整个决策学习过程。数据并行的步骤是:
水平分区数据。
工作人员使用本地数据构建本地直方图。
合并所有本地直方图的全局直方图。
从合并的全局直方图中找到最佳分割,然后执行分割。
传统数据并行的不足之处:
LightGBM 中的数据并行
我们减少了 LightGBM 中数据并行的通信成本:
LightGBM 不使用“合并所有本地直方图的全局直方图”,而是使用“减少分散”来合并不同(非重叠)特征的直方图给不同的工作者。然后工作者在本地合并的直方图上找到本地最佳分割,并同步全局最佳分割。
如前所述,LightGBM 使用直方图减法来加速训练。基于此,我们只需传递一个叶子的直方图,并通过减法获得其邻居的直方图。
总的来说,LightGBM 中的数据并行具有时间复杂度 O(0.5 * #特征 * #箱)。
投票并行
投票并行进一步将`数据并行 <#data-parallel>`__中的通信成本降低为常数成本。它使用两阶段投票来减少特征直方图的通信成本[10]。
GPU 支持
感谢 @huanzhang12 为此功能做出的贡献。请阅读 [11] 以获取更多详情。
应用程序和指标
LightGBM 支持以下应用:
回归问题中,目标函数是 L2 损失
二元分类中,目标函数是 logloss
多分类
交叉熵,目标函数是logloss,并支持对非二进制标签的训练
LambdaRank,目标函数是带有NDCG的LambdaRank
LightGBM 支持以下指标:
L1 损失
L2 损失
对数损失
分类错误率
AUC
NDCG
地图
多类对数损失
多类错误率
AUC-mu
(v3.0.0 新增)平均精度
(v3.1.0 新增)公平
Huber
泊松
分位数
MAPE
库尔贝克-莱布勒
Gamma
Tweedie
更多详情,请参阅 参数。
其他功能
在树生长时限制
max_depth的树深度L1/L2 正则化
Bagging
列(特征)子样本
继续使用输入的 GBDT 模型进行训练
继续训练输入的分数文件
加权训练
训练期间的验证指标输出
多重验证数据
多个指标
早停(训练和预测)
预测叶索引
更多详情,请参阅 参数。
参考文献
[1] 柯国霖, 孟奇, 托马斯·芬利, 王泰峰, 陈伟, 马维东, 叶启伟, 刘铁岩. “LightGBM: 一种高效的梯度提升决策树.” 神经信息处理系统进展 30 (NIPS 2017), 页码 3149-3157.
[2] Mehta, Manish, Rakesh Agrawal, 和 Jorma Rissanen. “SLIQ: 一个用于数据挖掘的快速可扩展分类器.” 扩展数据库技术国际会议. Springer Berlin Heidelberg, 1996.
[3] Shafer, John, Rakesh Agrawal, 和 Manish Mehta. “SPRINT: 数据挖掘的可扩展并行分类器.” Proc. 1996 Int. Conf. 超大数据库. 1996.
[4] Ranka, Sanjay, 和 V. Singh. “CLOUDS: 一种用于大数据集的决策树分类器.” 第四届知识发现与数据挖掘会议论文集. 1998.
[5] Machado, F. P. “高效并行决策树构建的通信和内存优化。” (2003).
[6] Li, Ping, Qiang Wu, 和 Christopher J. Burges. “Mcrank: 使用多分类和梯度提升进行排序学习.” 神经信息处理系统进展 20 (NIPS 2007).
[7] Shi, Haijian. “最佳优先决策树学习.” 博士论文. 怀卡托大学, 2007.
[8] Walter D. Fisher. “On Grouping for Maximum Homogeneity”. Journal of the American Statistical Association. Vol. 53, No. 284 (Dec., 1958), pp. 789-798.
[9] Thakur, Rajeev, Rolf Rabenseifner, 和 William Gropp. “Optimization of collective communication operations in MPICH”. International Journal of High Performance Computing Applications 19.1 (2005), pp. 49-66.
[10] 齐萌, 柯国霖, 王泰峰, 陈伟, 叶启伟, 马志明, 刘铁岩. “一种高效的决策树并行算法”. 《神经信息处理系统进展》29卷 (NIPS 2016), 第1279-1287页.
[11] Huan Zhang, Si Si 和 Cho-Jui Hsieh. “GPU 加速大规模树提升”. SysML 会议, 2018.