非支配排序遗传算法 III (NSGA-III)¶
非支配排序遗传算法 III (NSGA-III) [Deb2014] 在 deap.tools.selNSGA3() 函数中实现。这个例子展示了如何在 DEAP 中使用它进行多目标优化。
问题定义¶
首先,我们需要定义我们要解决的问题。我们将使用论文中测试的第一个问题,即具有 k = 10 和 p = 12 的3目标DTLZ2。我们将使用 pymop 进行问题实现,因为它提供了我们将用于计算算法性能的精确Pareto前沿。
PROBLEM = "dtlz2"
NOBJ = 3
K = 10
NDIM = NOBJ + K - 1
P = 12
H = factorial(NOBJ + P - 1) / (factorial(P) * factorial(NOBJ - 1))
BOUND_LOW, BOUND_UP = 0.0, 1.0
problem = pymop.factory.get_problem(PROBLEM, n_var=NDIM, n_obj=NOBJ)
算法参数¶
然后我们定义算法的各种参数,包括种群大小设置为大于 H 的第一个 4 的倍数,代数和变异概率。
MU = int(H + (4 - H % 4))
NGEN = 400
CXPB = 1.0
MUTPB = 1.0
类和工具¶
接下来,NSGA-III 选择需要一组参考点。参考点集用于引导进化过程在目标空间中创建均匀的 Pareto 前沿。
ref_points = tools.uniform_reference_points(NOBJ, P)
下一张图展示了一个参考点集的例子,其中 p = 12。十字表示乌托邦点 (0, 0, 0)。
与任何 DEAP 程序一样,我们需要用我们优化所需的个体类型来填充创建器。在这种情况下,我们将使用基本的列表基因型和最小化适应度。
creator.create("FitnessMin", base.Fitness, weights=(-1.0,) * NOBJ)
creator.create("Individual", list, fitness=creator.FitnessMin)
此外,我们需要用初始化、变异和选择操作符来填充进化工具箱。注意我们是如何向NSGA-III选择方案提供参考点集的。
def uniform(low, up, size=None):
try:
return [random.uniform(a, b) for a, b in zip(low, up)]
except TypeError:
return [random.uniform(a, b) for a, b in zip([low] * size, [up] * size)]
toolbox = base.Toolbox()
toolbox.register("attr_float", uniform, BOUND_LOW, BOUND_UP, NDIM)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.attr_float)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("evaluate", problem.evaluate, return_values_of=["F"])
toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=30.0)
toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=20.0, indpb=1.0/NDIM)
toolbox.register("select", tools.selNSGA3, ref_points=ref_points)
进化¶
进化过程的主要部分与其他DEAP示例大致相似。所使用的算法接近于 eaSimple() 算法,因为交叉和变异应用于每个个体(见上文变异概率)。然而,选择是从父代和子代种群中进行的,而不是完全用子代替换父代。
def main(seed=None):
random.seed(seed)
# Initialize statistics object
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", numpy.mean, axis=0)
stats.register("std", numpy.std, axis=0)
stats.register("min", numpy.min, axis=0)
stats.register("max", numpy.max, axis=0)
logbook = tools.Logbook()
logbook.header = "gen", "evals", "std", "min", "avg", "max"
pop = toolbox.population(n=MU)
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in pop if not ind.fitness.valid]
fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
# Compile statistics about the population
record = stats.compile(pop)
logbook.record(gen=0, evals=len(invalid_ind), **record)
print(logbook.stream)
# Begin the generational process
for gen in range(1, NGEN):
offspring = algorithms.varAnd(pop, toolbox, CXPB, MUTPB)
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
# Select the next generation population from parents and offspring
pop = toolbox.select(pop + offspring, MU)
# Compile statistics about the new population
record = stats.compile(pop)
logbook.record(gen=gen, evals=len(invalid_ind), **record)
print(logbook.stream)
return pop, logbook
最后,我们可以看看最终的人口
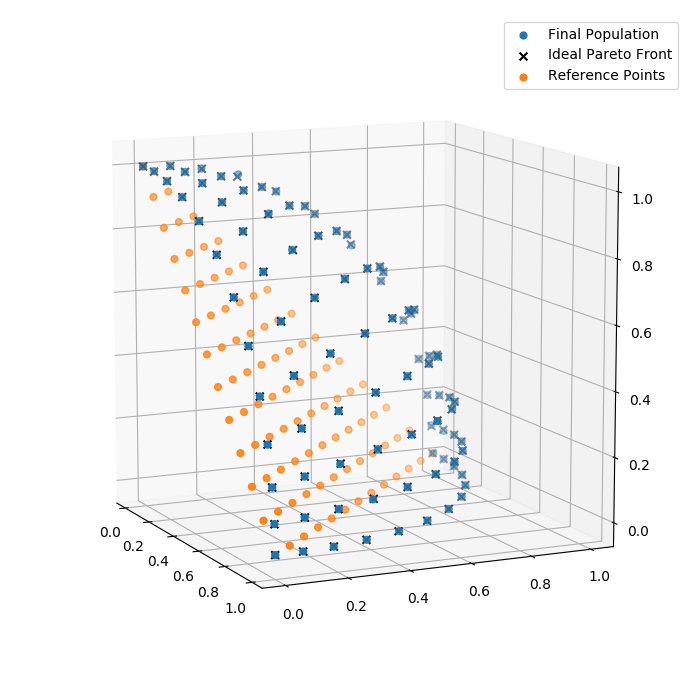
高维目标空间¶
NSGA-III 需要一个依赖于目标数量的参考点集。即使对于相对低维的目标空间,这个点集也可能变得非常大。例如,一个具有均匀参考点集的 15 维目标空间,如果 p = 4,将有 3060 个点。为了避免这种情况并减少算法的运行时间 [Deb2014],建议将参考点集与较低的 p 值结合。在 DEAP 中,我们可以通过以下方式组合多个均匀点集:
# Parameters
NOBJ = 3
P = [2, 1]
SCALES = [1, 0.5]
# Create, combine and removed duplicates
ref_points = [tools.uniform_reference_points(NOBJ, p, s) for p, s in zip(P, SCALES)]
ref_points = numpy.concatenate(ref_points, axis=0)
_, uniques = numpy.unique(ref_points, axis=0, return_index=True)
ref_points = ref_points[uniques]
这将生成以下参考点集,包含两个基础的均匀分布:一个在全尺度,另一个在半尺度。
结论¶
这就是使用 DEAP 的 NSGA-III 算法,现在你可以利用 DEAP 进行多目标优化的强大功能了。如果你感兴趣,可以复制 示例 并更改评估函数,尝试将其应用于你自己的问题。