进化工具¶

The tools 模块包含了进化算法的操作符。它们用于修改、选择和移动个体在其环境中的位置。它包含的操作符可以直接在 Toolbox 中使用。除了基本操作符外，该模块还包含一些实用工具，以通过 Statistics、HallOfFame 和 History 来增强基本算法。

运算符¶

操作集执行的是转换或选择个体的最小工作。这意味着，例如，将两个个体提供给交叉操作将在原地转换这些个体。使后代独立于其父代并使适应度无效的责任留给了用户，通常在算法中通过调用 toolbox.clone() 来复制个体，并通过删除个体的适应度的 values 属性来使其无效。

以下是DEAP中已实现的运算符列表，

初始化	交叉	突变	选择	迁移
`initRepeat()`	`cxOnePoint()`	`mutGaussian()`	`selTournament()`	`migRing()`
`initIterate()`	`cxTwoPoint()`	`mutShuffleIndexes()`	`selRoulette()`
`initCycle()`	`cxUniform()`	`mutFlipBit()`	`selNSGA2()`
	`cxPartialyMatched()`	`mutPolynomialBounded()`	`selNSGA3()`
	`cxUniformPartialyMatched()`	`mutUniformInt()`	`selSPEA2()`
	`cxOrdered()`	`mutESLogNormal()`	`selRandom()`
	`cxBlend()`		`selBest()`
	`cxESBlend()`		`selWorst()`
	`cxESTwoPoint()`		`selTournamentDCD()`
	`cxSimulatedBinary()`		`selDoubleTournament()`
	`cxSimulatedBinaryBounded()`		`selStochasticUniversalSampling()`
	`cxMessyOnePoint()`		`selLexicase()`
			`selEpsilonLexicase()`
			`selAutomaticEpsilonLexicase()`

以及遗传编程特定的操作符。

初始化	交叉	突变	Bloat 控制
`genFull()`	`cxOnePoint()`	`mutShrink()`	`staticLimit()`
`genGrow()`	`cxOnePointLeafBiased()`	`mutUniform()`	`selDoubleTournament()`
`genHalfAndHalf()`	`cxSemantic()`	`mutNodeReplacement()`
		`mutEphemeral()`
		`mutInsert()`
		`mutSemantic()`

初始化¶

deap.tools.initRepeat(container, func, n)[源代码]¶

调用函数 func n 次，并将结果返回在容器类型 container 中

参数:

container – 从 func 中放入数据的类型。
func – 将被调用 n 次以填充容器的函数。
n – 重复 func 的次数。

返回:

一个包含从 func 获取的数据的容器实例。

此辅助函数可以与工具箱结合使用，以注册填充容器的生成器，作为个体或群体。

>>> import random
>>> random.seed(42)
>>> initRepeat(list, random.random, 2) 
...                                    
[0.6394..., 0.0250...]

更多示例请参阅浮动列表和人口教程。

deap.tools.initIterate(container, generator)[源代码]¶

使用可迭代对象作为唯一参数调用函数 container。该可迭代对象必须由方法或对象 generator 返回。

参数:

container – 从 func 中放入数据的类型。
generator – 一个返回可迭代对象（列表、元组等）的函数，该可迭代对象的内容将填充容器。

返回:

一个包含从生成器填充数据的容器实例。

此辅助函数可以与工具箱结合使用，以注册填充容器的生成器，作为个体或群体。

>>> import random
>>> from functools import partial
>>> random.seed(42)
>>> gen_idx = partial(random.sample, range(10), 10)
>>> initIterate(list, gen_idx)      
[1, 0, 4, 9, 6, 5, 8, 2, 3, 7]

更多示例请参见排列和算术表达式教程。

deap.tools.initCycle(container, seq_func, n=1)[源代码]¶

调用函数 container ，并传入一个生成器函数，该生成器函数对应于调用 seq_func 中的函数 n 次。

参数:

container – 从 func 中放入数据的类型。
seq_func – 一个函数对象列表，按顺序调用以填充容器。
n – 遍历函数列表的次数。

返回:

一个包含从函数返回的数据的容器实例。

此辅助函数可以与工具箱结合使用，以注册填充容器的生成器，作为个体或群体。

>>> func_seq = [lambda:1 , lambda:'a', lambda:3]
>>> initCycle(list, func_seq, n=2)
[1, 'a', 3, 1, 'a', 3]

请参阅一个时髦的教程以获取示例。

deap.gp.genFull(pset, min_, max_, type_=None)[源代码]¶

生成一个表达式，其中每个叶子的深度在 min 和 max 之间相同。

参数:

pset – 从中选择原语的原语集。
min – 生成树的最小高度。
max – 生成树的最大高度。
type – The type that should return the tree when called, when None (default) the type of :pset: (pset.ret) is assumed.

返回:

一个所有叶子都在同一深度的完整树。

deap.gp.genGrow(pset, min_, max_, type_=None)[源代码]¶

生成一个表达式，其中每个叶子节点的深度可能在 min 和 max 之间不同。

参数:

pset – 从中选择原语的原语集。
min – 生成树的最小高度。
max – 生成树的最大高度。
type – The type that should return the tree when called, when None (default) the type of :pset: (pset.ret) is assumed.

返回:

一棵成熟的树，其叶子可能在不同的深度。

deap.gp.genHalfAndHalf(pset, min_, max_, type_=None)[源代码]¶

使用 PrimitiveSet pset 生成一个表达式。一半的时间，表达式使用 genGrow() 生成，另一半时间，表达式使用 genFull() 生成。

参数:

pset – 从中选择原语的原语集。
min – 生成树的最小高度。
max – 生成树的最大高度。
type – The type that should return the tree when called, when None (default) the type of :pset: (pset.ret) is assumed.

返回:

无论是完整的还是成熟的树。

deap.gp.genRamped(pset, min_, max_, type_=None)[源代码]¶: 1.0 版后已移除: 该函数已被重命名。请使用 genHalfAndHalf() 代替。

交叉¶

deap.tools.cxOnePoint(ind1, ind2)[源代码]¶

对输入的序列个体执行单点交叉操作。两个个体在原地被修改。生成的个体将分别具有对方的长度。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。

返回:

一对两个人的元组。

此函数使用了来自 Python 基础 random 模块的 randint() 函数。

deap.tools.cxTwoPoint(ind1, ind2)[源代码]¶

对输入的序列个体执行两点交叉操作。两个个体在原地进行修改，并且两者都保持其原始长度。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。

返回:

一对两个人的元组。

此函数使用了 Python 基础 random 模块中的 randint() 函数。

deap.tools.cxTwoPoints(ind1, ind2)[源代码]¶: 1.0 版后已移除: 该函数已被重命名。请使用 cxTwoPoint() 代替。

deap.tools.cxUniform(ind1, ind2, indpb)[源代码]¶

执行一个均匀交叉操作，直接修改两个序列个体。属性根据 indpb 概率进行交换。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。
indpb – 每个属性交换的独立概率。

返回:

一对两个人的元组。

此函数使用来自 Python 基础 random 模块的 random() 函数。

deap.tools.cxPartialyMatched(ind1, ind2)[源代码]¶

对输入的个体执行部分匹配交叉（PMX）。两个个体在原地被修改。此交叉期望序列个体的索引，对于其他类型的个体，结果是不可预测的。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。

返回:

一对两个人的元组。

此外，这种交叉通过匹配两个父代在一定范围内的值对，并交换这些索引的值，从而生成两个子代。更多详情请参见 [Goldberg1985]。

此函数使用了来自 Python 基础 random 模块的 randint() 函数。

[Goldberg1985]

Goldberg 和 Lingel, “等位基因、基因座和旅行商问题”, 1985.

deap.tools.cxUniformPartialyMatched(ind1, ind2, indpb)[源代码]¶

对输入的个体执行一致部分匹配交叉（UPMX）。两个个体在原地被修改。此交叉期望序列个体为索引，对于其他类型的个体，结果是不可预测的。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。

返回:

一对两个人的元组。

此外，这种交叉操作通过在两个父代中随机选择一对值，并以 indpb 的概率匹配这些值，并交换这些索引的值，从而生成两个子代。更多详情请参见 [Cicirello2000]。

此函数使用了 python 基础 random 模块中的 random() 和 randint() 函数。

[Cicirello2000]

Cicirello 和 Smith, “建模GA性能以进行控制参数优化”, 2000.

deap.tools.cxOrdered(ind1, ind2)[源代码]¶

对输入的个体执行有序交叉（OX）。这两个个体在原地被修改。此交叉期望序列个体为索引，对于其他类型的个体，结果是不可预测的。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。

返回:

一对两个人的元组。

此外，这种交叉操作在输入个体中生成空洞。当一个个体的属性位于另一个个体的两个交叉点之间时，就会创建一个空洞。然后它旋转元素，使得所有空洞都位于交叉点之间，并按顺序用移除的元素填充它们。更多细节请参见 [Goldberg1989]。

此函数使用了来自 Python 基础 random 模块的 sample() 函数。

[Goldberg1989]

Goldberg. 遗传算法在搜索、优化和机器学习中的应用。Addison Wesley, 1989

deap.tools.cxBlend(ind1, ind2, alpha)[源代码]¶

执行一个混合交叉操作，原地修改输入的个体。混合交叉期望序列个体为浮点数。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。
alpha – 在父属性两侧的每个属性可以绘制新值的区间范围。

返回:

一对两个人的元组。

此函数使用来自 Python 基础 random 模块的 random() 函数。

deap.tools.cxESBlend(ind1, ind2, alpha)[源代码]¶

对个体和策略都执行混合交叉操作。个体应为一个序列，并且必须有一个序列 策略 属性。在此函数调用后应调整最小策略，考虑使用装饰器。

参数:

ind1 – 参与交叉的第一个进化策略。
ind2 – 参与交叉的第二种进化策略。
alpha – 在父属性两侧的每个属性可以绘制新值的区间范围。

返回:

两种进化策略的元组。

此函数使用来自 Python 基础 random 模块的 random() 函数。

deap.tools.cxESTwoPoint(ind1, ind2)[源代码]¶

对个体及其策略执行经典的二点交叉。个体应为序列，并且必须具有序列 策略 属性。个体和策略的交叉点是相同的。

参数:

ind1 – 参与交叉的第一个进化策略。
ind2 – 参与交叉的第二种进化策略。

返回:

两种进化策略的元组。

此函数使用了来自 Python 基础 random 模块的 randint() 函数。

deap.tools.cxESTwoPoints(ind1, ind2)[源代码]¶: 1.0 版后已移除: 该函数已被重命名。请使用 cxESTwoPoint() 代替。

deap.tools.cxSimulatedBinary(ind1, ind2, eta)[源代码]¶

执行一个模拟二进制交叉操作，直接修改输入个体的值。模拟二进制交叉期望输入的个体是浮点数的序列。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。
eta – 交叉的拥挤程度。高 eta 会产生与父母相似的孩子，而低 eta 会产生大不相同的解决方案。

返回:

一对两个人的元组。

此函数使用来自 Python 基础 random 模块的 random() 函数。

deap.tools.cxSimulatedBinaryBounded(ind1, ind2, eta, low, up)[源代码]¶

执行一个模拟二进制交叉操作，直接修改输入个体的值。模拟二进制交叉期望输入的个体是浮点数的序列。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。
eta – 交叉的拥挤程度。高 eta 会产生与父母相似的孩子，而低 eta 会产生大不相同的解决方案。
low – 一个值或一个 sequence 的值，它是搜索空间的下限。
up – 一个值或一个 sequence 的值，它是搜索空间的上限。

返回:

一对两个人的元组。

此函数使用来自 Python 基础 random 模块的 random() 函数。

备注

此实现与Deb提供的原始NSGA-II C代码中的实现类似。

deap.tools.cxMessyOnePoint(ind1, ind2)[源代码]¶

对序列个体执行单点交叉。交叉操作在大多数情况下会改变个体的大小。两个个体在原地被修改。

参数:

ind1 – 参与跨界合作的第一位个人。
ind2 – 参与跨界合作的第二位个人。

返回:

一对两个人的元组。

此函数使用了来自 Python 基础 random 模块的 randint() 函数。

deap.gp.cxOnePoint(ind1, ind2)[源代码]¶

在每个个体中随机选择交叉点，并在每个个体之间以该点为根交换每个子树。

参数:

ind1 – 第一个参与交叉的树。
ind2 – 参与交叉的第二棵树。

返回:

两个树的元组。

deap.gp.cxOnePointLeafBiased(ind1, ind2, termpb)[源代码]¶

在每个个体中随机选择交叉点，并在每个个体之间以该点为根交换每个子树。

参数:

ind1 – 首次参与交叉的类型化树。
ind2 – 参与交叉的第二个类型化树。
termpb – 选择一个终端节点（叶子）的概率。

返回:

两个类型化树的元组。

当节点是强类型时，操作符会确保第二个节点的类型与第一个节点的类型相对应。

参数 termpb 设置在终端或非终端交叉点之间选择的概率。例如，根据 Koza 的定义，非终端原语在 90% 的交叉点被选中，终端在 10% 的交叉点被选中，因此 termpb 应设置为 0.1。

deap.gp.cxSemantic(ind1, ind2, gen_func=<function genGrow>, pset=None, min=2, max=6)[源代码]¶

语义交叉算子的实现 [几何语义遗传编程, Moraglio 等人, 2012] 后代1 = random_tree1 * ind1 + (1 - random_tree1) * ind2 后代2 = random_tree1 * ind2 + (1 - random_tree1) * ind1

参数:

ind1 – 第一个父级
ind2 – 第二父级
gen_func – 负责生成在变异过程中使用的随机树的函数
pset – 原始集合，包含在进化过程中使用的终端和操作数
min – 随机树的最小深度
max – 随机树的最大深度

返回:

后代

变异的后代包含父母

>>> import operator
>>> def lf(x): return 1 / (1 + math.exp(-x));
>>> pset = PrimitiveSet("main", 2)
>>> pset.addPrimitive(operator.sub, 2)
>>> pset.addTerminal(3)
>>> pset.addPrimitive(lf, 1, name="lf")
>>> pset.addPrimitive(operator.add, 2)
>>> pset.addPrimitive(operator.mul, 2)
>>> ind1 = genGrow(pset, 1, 3)
>>> ind2 = genGrow(pset, 1, 3)
>>> new_ind1, new_ind2 = cxSemantic(ind1, ind2, pset=pset, max=2)
>>> ctr = sum([n.name == ind1[i].name for i, n in enumerate(new_ind1)])
>>> ctr == len(ind1)
True
>>> ctr = sum([n.name == ind2[i].name for i, n in enumerate(new_ind2)])
>>> ctr == len(ind2)
True

突变¶

deap.tools.mutGaussian(individual, mu, sigma, indpb)[源代码]¶

此函数对输入个体应用均值为 mu 和标准差为 sigma 的高斯变异。此变异期望一个由实值属性组成的序列个体。indpb 参数是每个属性被变异的概率。

参数:

individual – 要变异的个体。
mu – 高斯加法变异的均值或 sequence 均值。
sigma – 标准差或 sequence 的高斯加法变异的标准差。
indpb – 每个属性独立变异的概率。

返回:

一个单独个体的元组。

此函数使用了 python 基础 random 模块中的 random() 和 gauss() 函数。

deap.tools.mutShuffleIndexes(individual, indpb)[源代码]¶

打乱输入个体的属性并返回变异体。individual 应为一个序列。indpb 参数是每个属性被移动的概率。通常这种变异应用于索引向量。

参数:

individual – 要变异的个体。
indpb – 每个属性独立地交换到另一个位置的概率。

返回:

一个单独个体的元组。

此函数使用了 python 基础 random 模块中的 random() 和 randint() 函数。

deap.tools.mutFlipBit(individual, indpb)[源代码]¶

翻转输入个体的属性值并返回突变体。individual 应为一个序列，并且在对其调用 not 运算符后，属性的值应保持有效。indpb 参数是每个属性被翻转的概率。这种突变通常应用于布尔个体。

参数:

individual – 要变异的个体。
indpb – 每个属性被翻转的独立概率。

返回:

一个单独个体的元组。

此函数使用来自 Python 基础 random 模块的 random() 函数。

deap.tools.mutUniformInt(individual, low, up, indpb)[源代码]¶

通过以概率 indpb 替换属性，将个体变异为在 low 和 up 之间均匀抽取的整数，包括 low 和 up。

参数:

individual – 序列个体将被突变。
low – 范围的下限或下限的 sequence ，从中绘制新的整数。
up – 范围的上限或一系列上限，从中抽取新的整数。
indpb – 每个属性独立变异的概率。

返回:

一个单独个体的元组。

deap.tools.mutPolynomialBounded(individual, eta, low, up, indpb)[源代码]¶

多项式变异，如Deb在C语言中实现的原始NSGA-II算法中所实现的那样。

参数:

individual – 序列个体将被突变。
eta – 变异的拥挤程度。高 eta 将产生一个与其父代相似的变异体，而低 eta 将产生一个差异更大的解决方案。
low – 一个值或一个 sequence 的值，它是搜索空间的下限。
up – 一个值或一个 sequence 的值，它是搜索空间的上限。

返回:

一个单独个体的元组。

deap.tools.mutESLogNormal(individual, c, indpb)[源代码]¶

根据[Beyer2002]_中的描述，按照其:attr:strategy`属性对进化策略进行变异。首先，根据扩展的对数正态规则对策略进行变异，:math:\boldsymbol{sigma}_t = \exp(\tau_0 mathcal{N}_0(0, 1)) \left[ \sigma_{t-1, 1}\exp(\tau mathcal{N}_1(0, 1)), ldots, \sigma_{t-1, n} \exp(\tau mathcal{N}_n(0, 1))\right]`，其中:math:\tau_0 = \frac{c}{\sqrt{2n}}`和:math:\tau = \frac{c}{\sqrt{2\sqrt{n}}}`，然后个体通过均值为0且标准差为:math:\boldsymbol{sigma}_{t}`（其当前策略）的正态分布进行变异。当使用:math:`(10, 100)`进化策略时，推荐的选项是``c=1` [Beyer2002] [Schwefel1995]。

参数:

individual – 序列个体将被突变。
c – 学习参数。
indpb – 每个属性独立变异的概率。

返回:

一个单独个体的元组。

[Beyer2002] (1,2)

Beyer 和 Schwefel, 2002, 进化策略 - 全面介绍

[Schwefel1995]

Schwefel, 1995, 《进化与最优寻求》。Wiley, 纽约, NY

deap.gp.mutShrink(individual)[源代码]¶

此操作符通过随机选择一个分支，并用该分支的一个参数（也是随机选择的）替换它，从而缩小个体。

参数:: individual – 要缩小的树。
返回:: 一个树的元组。

deap.gp.mutUniform(individual, expr, pset)[源代码]¶

在树 individual 中随机选择一个点，然后使用方法 expr() 生成的表达式替换该点的子树作为根。

参数:

individual – 要变异的树。
expr – 一个可以在调用时生成表达式的函数对象。

返回:

一个树的元组。

deap.gp.mutNodeReplacement(individual, pset)[源代码]¶

用从 individual 中随机选择的具有相同数量参数的原始元素替换 individual 中的一个随机选择的原始元素，该原始元素来自 individual 的 pset 属性。

参数:: individual – 要被变异的普通或类型化树。
返回:: 一个树的元组。

deap.gp.mutEphemeral(individual, mode)[源代码]¶

此操作符作用于树 individual 的常量。在 mode "one" 中，它将通过调用其生成器函数来改变个体瞬态常量之一的值。在 mode "all" 中，它将改变所有瞬态常量的值。

参数:

individual – 要被变异的普通或类型化树。
mode – 一个字符串，用于指示更改 "one" 或 "all" 临时常量。

返回:

一个树的元组。

deap.gp.mutInsert(individual, pset)[源代码]¶

在 individual 的随机位置插入一个新分支。所选位置的子树被用作创建的子树的子节点，因此这实际上是插入而不是替换。请注意，原始子树将成为插入的新原语的子节点之一，但不一定排在首位（如果新原语有多个子节点，则其位置是随机选择的）。

参数:: individual – 要被变异的普通或类型化树。
返回:: 一个树的元组。

deap.gp.mutSemantic(individual, gen_func=<function genGrow>, pset=None, ms=None, min=2, max=6)[源代码]¶

语义变异操作符的实现。[几何语义遗传编程，Moraglio 等人，2012] mutated_individual = individual + logistic * (random_tree1 - random_tree2)

参数:

individual – 个体变异
gen_func – 负责生成在变异过程中使用的随机树的函数
pset – 原始集合，包含在进化过程中使用的终端和操作数
ms – 变异步骤
min – 随机树的最小深度
max – 随机树的最大深度

返回:

变异个体

变异体包含原始个体

>>> import operator
>>> def lf(x): return 1 / (1 + math.exp(-x));
>>> pset = PrimitiveSet("main", 2)
>>> pset.addPrimitive(operator.sub, 2)
>>> pset.addTerminal(3)
>>> pset.addPrimitive(lf, 1, name="lf")
>>> pset.addPrimitive(operator.add, 2)
>>> pset.addPrimitive(operator.mul, 2)
>>> individual = genGrow(pset, 1, 3)
>>> mutated = mutSemantic(individual, pset=pset, max=2)
>>> ctr = sum([m.name == individual[i].name for i, m in enumerate(mutated[0])])
>>> ctr == len(individual)
True

选择¶

deap.tools.selTournament(individuals, k, tournsize, fit_attr='fitness')[源代码]¶

从 tournsize 个随机选择的个体中选择最佳个体，重复 k 次。返回的列表包含对输入 individuals 的引用。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
tournsize – 每个锦标赛参与者的数量。
fit_attr – 用作选择标准的个人属性

返回:

一个精选个体的列表。

此函数使用了来自 Python 基础 random 模块的 choice() 函数。

deap.tools.selRoulette(individuals, k, fit_attr='fitness')[源代码]¶

从输入的 individuals 中选择 k 个个体，使用轮盘赌的 k 次旋转。选择仅基于每个个体的第一个目标。返回的列表包含对输入 individuals 的引用。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
fit_attr – 用作选择标准的个人属性

返回:

一个精选个体的列表。

此函数使用来自 Python 基础 random 模块的 random() 函数。

警告

根据定义，轮盘选择不能用于最小化问题，或者当适应度可能小于或等于0时。

deap.tools.selNSGA2(individuals, k, nd='standard')[源代码]¶

对 individuals 应用 NSGA-II 选择操作符。通常，individuals 的大小会大于 k，因为 individuals 中的任何个体在返回的列表中最多出现一次。使 individuals 的大小等于 k 除了根据前排名对种群进行排序外，不会有其他效果。返回的列表包含对输入 individuals 的引用。有关 NSGA-II 操作符的更多详细信息，请参见 [Deb2002]。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
nd – 指定要使用的非支配算法：’standard’ 或 ‘log’。

返回:

一个精选个体的列表。

[Deb2002]

Deb, Pratab, Agarwal, 和 Meyarivan, “一种快速精英非支配排序遗传算法用于多目标优化: NSGA-II”, 2002.

deap.tools.selNSGA3(individuals, k, ref_points, nd='log', best_point=None, worst_point=None, extreme_points=None, return_memory=False)[源代码]¶

如 [Deb2014] 所述，实现了 NSGA-III 选择。

此实现部分基于 lmarti/nsgaiii 。它与原始实现略有不同，因为它不使用内存来跟踪理想点和极点。这一选择是为了适应DEAP的功能API。关于NSGA-III的版本，请参见 selNSGA3WithMemory。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
ref_points – 用于细分的参考点。
nd – 指定要使用的非支配算法：’standard’ 或 ‘log’。
best_point – 在上一代中找到的最佳点。如果没有提供，则仅从当前个体中找到最佳点。
worst_point – 在前一代中找到的最差点。如果没有提供，则仅从当前个体中找到最差点。
extreme_points – 在前一代中找到的极值点。如果没有提供，则仅从当前个体中寻找极值点。
return_memory – 如果 True，除了选择的个体外，还会返回最佳、最差和极端点。

返回:

一个精选个体的列表。

返回:

如果 return_memory 是 True，则返回一个包含 best_point、worst_point 和 extreme_points 的命名元组。

你可以使用 uniform_reference_points() 函数生成参考点:

>>> ref_points = tools.uniform_reference_points(nobj=3, p=12)   
>>> selected = selNSGA3(population, k, ref_points)              

[Deb2014]

Deb, K., & Jain, H. (2014). 基于参考点非支配排序方法的进化多目标优化算法，第一部分：解决具有箱型约束的问题。IEEE 进化计算汇刊, 18(4), 577-601. doi:10.1109/TEVC.2013.2281535.

deap.tools.selNSGA3WithMemory(ref_points, nd='log')[源代码]¶

包含最佳、最差和极值点记忆的 NSGA-III 选择类版本。在工具箱中注册此操作符与经典操作符略有不同，它需要实例化类，而不仅仅是注册函数:

>>> from deap import base
>>> ref_points = uniform_reference_points(nobj=3, p=12)
>>> toolbox = base.Toolbox()
>>> toolbox.register("select", selNSGA3WithMemory(ref_points))

deap.tools.uniform_reference_points(nobj, p=4, scaling=None)[源代码]¶: 在超平面上均匀生成参考点，每个轴在1处相交。缩放因子用于组合多层参考点。

deap.tools.selSPEA2(individuals, k)[源代码]¶

对 individuals 应用 SPEA-II 选择操作符。通常，individuals 的大小会大于 n，因为 individuals 中的任何个体在返回的列表中最多出现一次。使 individuals 的大小等于 n 除了根据强度 Pareto 方案对种群进行排序外，不会有其他效果。返回的列表包含对输入 individuals 的引用。有关 SPEA-II 操作符的更多详细信息，请参见 [Zitzler2001]。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。

返回:

一个精选个体的列表。

[Zitzler2001]

Zitzler, Laumanns 和 Thiele, “SPEA 2: 改进强度帕累托进化算法”, 2001.

deap.tools.selRandom(individuals, k)[源代码]¶

从输入的 individuals 中随机选择 k 个个体，允许重复选择。返回的列表包含对输入 individuals 的引用。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。

返回:

一个精选个体的列表。

此函数使用了来自 Python 基础 random 模块的 choice() 函数。

deap.tools.selBest(individuals, k, fit_attr='fitness')[源代码]¶

从输入的 individuals 中选择 k 个最佳个体。返回的列表包含对输入 individuals 的引用。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
fit_attr – 用作选择标准的个人属性

返回:

包含 k 个最佳个体的列表。

deap.tools.selWorst(individuals, k, fit_attr='fitness')[源代码]¶

从输入的 individuals 中选择 k 个最差的个体。返回的列表包含对输入 individuals 的引用。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
fit_attr – 用作选择标准的个人属性

返回:

包含k个最差个体的列表。

deap.tools.selDoubleTournament(individuals, k, fitness_size, parsimony_size, fitness_first, fit_attr='fitness')[源代码]¶

锦标赛选择使用个体的大小来区分好的解决方案。这种锦标赛显然对固定长度的表示是无效的，但已被证明能显著减少个体的过度增长，特别是在GP中，它可以作为一种膨胀控制技术使用（参见[Luke2002fighting]_）。此选择操作符实现了本文中介绍的双锦标赛技术。

核心原则是使用正常的锦标赛选择，但使用一个特殊的采样函数来选择候选人，这是基于个体大小的另一个锦标赛。为了确保选择压力不过高，大小锦标赛的大小（评估的候选人数量）可以是1到2之间的实数。在这种情况下，两个个体中较小的个体将以概率 size_tourn_size/2 被选中。例如，如果 size_tourn_size 设置为1.4，那么较小的个体将有0.7的概率被选中。

备注

在GP中，已经证明当这个操作符与某种深度限制结合时，会产生更好的结果。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
fitness_size – 参加每场健身比赛的人数
parsimony_size – 每个规模锦标赛中参与的个体数量。该值必须是一个在范围 [1,2] 内的实数，详见上文。
fitness_first – 如果第一个比赛应该是适应度比赛（即产生参加大小比赛的候选者的适应度比赛），请将此设置为 True。将其设置为 False 将表现为相反的情况（大小比赛为适应度比赛提供候选者）。已经表明，在大多数情况下，此参数没有显著影响（参见 [Luke2002fighting]）。
fit_attr – 用作选择标准的个人属性

返回:

一个精选个体的列表。

[Luke2002fighting] (1,2)

Luke 和 Panait, 2002, 使用非参数简约压力对抗膨胀

deap.tools.selStochasticUniversalSampling(individuals, k, fit_attr='fitness')[源代码]¶

从输入的 individuals 中选择 k 个个体。选择是通过使用一个随机值来均匀间隔地采样所有个体来进行的。返回的列表包含对输入 individuals 的引用。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
fit_attr – 用作选择标准的个人属性

返回:

一个精选个体的列表。

此函数使用了来自 Python 基础 random 模块的 uniform() 函数。

deap.tools.selTournamentDCD(individuals, k)[源代码]¶

基于支配（D）的锦标赛选择在两个个体之间进行，如果两个个体不相互支配，则根据拥挤距离（CD）进行选择。*个体*序列的长度必须是4的倍数，仅当k等于个体长度时。从选定个体的开始，两个连续的个体会不同（假设输入列表中的所有个体都是唯一的）。输入列表中的每个个体不会被选择超过两次。

此选择要求个体具有 crowding_dist 属性，该属性可以通过 assignCrowdingDist() 函数设置。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。必须小于或等于 len(individuals)。

返回:

一个精选个体的列表。

deap.tools.selLexicase(individuals, k)[源代码]¶

返回在随机顺序下逐个考虑适应度案例时表现最佳的个体。http://faculty.hampshire.edu/lspector/pubs/lexicase-IEEE-TEC.pdf

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。

返回:

一个精选个体的列表。

deap.tools.selEpsilonLexicase(individuals, k, epsilon)[源代码]¶

返回在随机顺序逐一考虑适应性案例时表现最佳的个体。需要一个epsilon参数。https://push-language.hampshire.edu/uploads/default/original/1X/35c30e47ef6323a0a949402914453f277fb1b5b0.pdf 实现了epsilon_y实现。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。

返回:

一个精选个体的列表。

deap.tools.selAutomaticEpsilonLexicase(individuals, k)[源代码]¶

返回在随机顺序逐一考虑适应性案例时表现最佳的个体。https://push-language.hampshire.edu/uploads/default/original/1X/35c30e47ef6323a0a949402914453f277fb1b5b0.pdf 实现了 lambda_epsilon_y 实现。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。

返回:

一个精选个体的列表。

deap.tools.sortNondominated(individuals, k, first_front_only=False)[源代码]¶

使用Deb等人提出的“快速非支配排序方法”将前 k 个个体排序到不同的非支配层级，参见 [Deb2002]。该算法的时间复杂度为 \(O(MN^2)\)，其中 \(M\) 是目标的数量，\(N\) 是个体的数量。

参数:

individuals – 可供选择的个人列表。
k – 要选择的个体数量。
first_front_only – If True sort only the first front and exit.

返回:

帕累托前沿列表（列表），第一个列表包含非支配个体。

[Deb2002]

Deb, Pratab, Agarwal, 和 Meyarivan, “一种快速精英非支配排序遗传算法用于多目标优化: NSGA-II”, 2002.

deap.tools.sortLogNondominated(individuals, k, first_front_only=False)[源代码]¶

使用Fortin等人（2013年）提出的广义减少运行时间复杂度的非支配排序算法对*个体*进行帕累托非支配前沿排序。

参数:: individuals – 可供选择的个人列表。
返回:: 帕累托前沿列表（列表），其中第一个列表是真实的帕累托前沿。

Bloat 控制¶

deap.gp.staticLimit(key, max_value)[源代码]¶

在GP树的某些测量上实现一个静态限制，如Koza在[Koza1989]中所定义。它可以用来装饰交叉和变异操作符。当生成一个无效（超过限制）的子代时，它会被其父母中的一个随机替换。

此操作符可用于避免树的高度超过90层时发生的内存错误（因为Python对调用栈深度有限制），因为它可以确保在种群中不会接受超过此限制的树，除非它在初始化时生成。

参数:

key – 用于获取所需值的函数。例如，在GP树中，可以使用 operator.attrgetter('height') 来设置深度限制，使用 len 来设置大小限制。
max_value – 给定测量的允许最大值。

返回:

一个可以使用 decorate() 应用于 GP 操作符的装饰器

备注

如果你想重现 Koza 所期望的精确行为，请将 key 设置为 operator.attrgetter('height') 并将 max_value 设置为 17。

[Koza1989]

J.R. Koza, 遗传编程 - 通过自然选择对计算机进行编程 (MIT Press, 剑桥, MA, 1992)

迁移¶

deap.tools.migRing(populations, k, selection[, replacement, migarray])[源代码]¶

在种群之间执行环形迁移。迁移首先使用指定的选择算子从每个种群中选择 k 个移民，然后通过这些移民替换 migarray 中关联种群的 k 个个体。如果没有指定替换算子，移民将替换种群中的移民，否则，移民将替换由替换算子选择的个体。如果提供了迁移数组，它应包含每个种群的索引一次且仅一次。如果没有提供迁移数组，它默认为串行环形迁移（1 – 2 – … – n – 1）。选择和替换函数使用签名 selection(populations[i], k) 和 replacement(populations[i], k) 调用。需要注意的是，替换策略必须选择 k 个不同的个体。例如，使用传统的锦标赛作为替换策略将产生不良效果，两个个体很可能会尝试进入同一个位置。

参数:

populations – 要进行迁移操作的（子）群体列表。
k – 要迁移的个体数量。
selection – 用于选择的函数。
replacement – The function to use to select which individuals will be replaced. If None (default) the individuals that leave the population are directly replaced.
migarray – 一个索引列表，指示列表中特定位置的个体去向。这默认为环形迁移。

统计¶

class deap.tools.Statistics([key])[源代码]¶

编译任意对象列表统计信息的对象。创建时，统计对象接收一个 key 参数，该参数用于获取将计算函数的值。如果未提供 key 参数，则默认为恒等函数。

键返回的值可能是一个多维对象，即：一个元组或列表，只要注册的统计函数支持它。因此，例如，在使用numpy统计函数时，可以直接计算多目标适应度的统计数据。

参数:: key – 一个用于访问计算统计量所依据的值的函数，可选。

>>> import numpy
>>> s = Statistics()
>>> s.register("mean", numpy.mean)
>>> s.register("max", max)
>>> s.compile([1, 2, 3, 4])     
{'max': 4, 'mean': 2.5}
>>> s.compile([5, 6, 7, 8])     
{'mean': 6.5, 'max': 8}

compile(data)[源代码]¶

将输入序列 data 应用于每个已注册的函数，并将结果作为字典返回。

参数:: data – 计算统计数据的物体序列。

register(name, function, *args, **kargs)[源代码]¶

注册一个函数，该函数将在每次调用 record() 时应用于序列。

参数:

name – 统计函数在统计对象字典中显示的名称。
function – 一个函数，将根据键预处理后的数据计算所需的统计信息。
argument – 一个或多个参数（以及关键字参数），在调用时自动传递给注册的函数，可选。

class deap.tools.MultiStatistics(**kargs)[源代码]¶

允许通过单次调用 compile() 计算多个键统计信息的 Statistics 对象字典。它接受一组键值对，将统计对象与唯一名称关联起来。然后可以使用此名称检索统计对象。

以下代码同时计算所提供对象的长度和第一个值的统计信息。

>>> from operator import itemgetter
>>> import numpy
>>> len_stats = Statistics(key=len)
>>> itm0_stats = Statistics(key=itemgetter(0))
>>> mstats = MultiStatistics(length=len_stats, item=itm0_stats)
>>> mstats.register("mean", numpy.mean, axis=0)
>>> mstats.register("max", numpy.max, axis=0)
>>> mstats.compile([[0.0, 1.0, 1.0, 5.0], [2.0, 5.0]])  
{'length': {'mean': 3.0, 'max': 4}, 'item': {'mean': 1.0, 'max': 2.0}}

compile(data)[源代码]¶

调用每个 Statistics 对象的 data 与 Statistics.compile()。

参数:: data – 计算统计数据的物体序列。

register(name, function, *args, **kargs)[源代码]¶

在每个 Statistics 对象中注册一个函数。

参数:

name – 统计函数在统计对象字典中显示的名称。
function – 一个函数，将根据键预处理后的数据计算所需的统计信息。
argument – 一个或多个参数（以及关键字参数），在调用时自动传递给注册的函数，可选。

日志簿¶

class deap.tools.Logbook[源代码]¶

进化记录作为字典的时间顺序列表。

可以通过 select() 方法检索数据，前提是提供适当的名称。

类 Logbook 也可能包含其他被称为章节的日志簿。章节用于存储与进化特定部分相关的信息。例如，在计算个体的不同组件的统计数据时（即 MultiStatistics），章节可以用来区分平均适应度和平均大小。

chapters¶

包含日志簿子部分的词典，这些子部分也是 Logbook 。当传递给 record 函数的键值参数的右侧是一个字典时，章节会自动创建。关键字决定了章节的名字。例如，以下行添加了一个名为“size”的新章节，该章节将包含字段“max”和“mean”。

logbook.record(gen=0, size={'max' : 10.0, 'mean' : 7.5})

要访问特定章节，请使用章节名称作为字典键。例如，要访问大小章节并选择平均值，请使用

logbook.chapters["size"].select("mean")

编译一个 MultiStatistics 对象会返回一个包含字典的字典，因此当使用关键字参数解包运算符 (**) 将此类对象记录在日志簿中时，章节将自动添加到日志簿中。:

>>> fit_stats = Statistics(key=attrgetter("fitness.values"))
>>> size_stats = Statistics(key=len)
>>> mstats = MultiStatistics(fitness=fit_stats, size=size_stats)
>>> # [...]
>>> record = mstats.compile(population)
>>> logbook.record(**record)
>>> print logbook
  fitness          length
------------    ------------
max     mean    max     mean
2       1       4       3

header¶

在使用 stream 和 __str__() 方法时，打印列的顺序。语法是一个包含字符串元素的单一可迭代对象。例如，对于之前定义的统计类，可以打印代数、适应度平均值和最大值，如下所示

logbook.header = ("gen", "mean", "max")

如果未设置，表头将使用所有字段构建，插入第一条数据时按任意顺序排列。可以通过将其设置为 None 来移除表头。

log_header¶: 指示日志簿在流式传输第一行或获取其整个字符串表示时是否输出头部。默认为 True。

pop(index=0)[源代码]¶

检索并删除元素 index。标题和流将调整为遵循修改后的状态。

参数:: item – 要移除的元素的索引，可选。默认为第一个元素。

你也可以使用以下语法来删除元素。:

del log[0]
del log[1::5]

record(**infos)[源代码]¶: 在日志簿中输入一个事件记录，作为键值对的列表。信息按时间顺序附加到一个列表中，作为字典。当一对中的值部分是字典时，字典中包含的信息将记录在一个章节中，该章节的标题为该对中键部分的名称。章节也是日志簿。

select(*names)[源代码]¶

返回与 Statistics 对象列表中每个字典的参数中提供的 names 相关联的值列表。每个名称按顺序返回一个列表。:

>>> log = Logbook()
>>> log.record(gen=0, mean=5.4, max=10.0)
>>> log.record(gen=1, mean=9.4, max=15.0)
>>> log.select("mean")
[5.4, 9.4]
>>> log.select("gen", "max")
([0, 1], [10.0, 15.0])

通过一个 MultiStatistics 对象，可以使用 chapters 成员来检索每个测量的统计数据：

>>> log = Logbook()
>>> log.record(**{'gen': 0, 'fit': {'mean': 0.8, 'max': 1.5},
... 'size': {'mean': 25.4, 'max': 67}})
>>> log.record(**{'gen': 1, 'fit': {'mean': 0.95, 'max': 1.7},
... 'size': {'mean': 28.1, 'max': 71}})
>>> log.chapters['size'].select("mean")
[25.4, 28.1]
>>> log.chapters['fit'].select("gen", "max")
([0, 1], [1.5, 1.7])

property stream¶

检索数据库中尚未流式传输的格式化条目，包括标题。:

>>> log = Logbook()
>>> log.append({'gen' : 0})
>>> print log.stream  
gen
0
>>> log.append({'gen' : 1})
>>> print log.stream  
1

名人堂¶

class deap.tools.HallOfFame(maxsize, similar=<built-in function eq>)[源代码]¶

名人堂包含了在进化过程中生活在种群中的最佳个体。它始终按字典顺序排序，因此名人堂的第一个元素是根据创建时提供的适应度权重，拥有最佳首次适应度值的个体。

插入操作是为了让旧个体优先于新个体。在任何时候都只保留每个个体的单一副本，两个个体之间的等价性由传递给 similar 参数的操作符决定。

参数:

maxsize – 在名人堂中保留的个体最大数量。
similar – 两个个体之间的等价运算符，可选。默认为运算符 operator.eq()。

类 HallOfFame 提供了一个类似于列表的接口（但并不完全是一个列表）。可以获取其长度，向前和向后迭代，以及从中获取项目或切片。

update(population)[源代码]¶

通过用 population 中的最佳个体替换其中的最差个体（如果它们更好）来更新名人堂。名人堂的大小保持不变。

参数:: population – 具有适应度属性的个体列表，用于更新名人堂。

insert(item)[源代码]¶

使用 bisect_right() 函数在名人堂中插入一个新的个体。插入的个体将被插入到相等个体的右侧。在名人堂中插入新个体时，也会保持名人堂的顺序。此方法**不会**检查名人堂的大小，也就是说，在一个已满的名人堂中插入新个体时，不会移除最差的个体以维持固定大小。

参数:: item – 具有适应度属性以插入名人堂的个体。

remove(index)[源代码]¶

从名人堂中移除指定的 index。

参数:: index – 一个整数，表示要移除的项目。

clear()[源代码]¶: 清除名人堂。

class deap.tools.ParetoFront([similar])[源代码]¶

帕累托前沿名人堂包含了所有在种群中曾经存在的非支配个体。这意味着帕累托前沿名人堂可以包含无限多的不同个体。

参数:: similar – 一个函数，用于告知帕累托前沿两个个体是否相似，可选。

如果在前端使用连续函数和连续域的情况下，其大小可能会变得非常大。为了限制个体数量，可以指定一个相似性函数，如果两个个体的基因型相似，则返回 True。在这种情况下，只有两个个体中的一个会被添加到名人堂中。默认的相似性函数是 operator.eq()。

由于，帕累托前沿的荣誉榜继承自 荣誉榜 ，它在每个时刻都是按字典顺序排序的。

update(population)[源代码]¶

通过添加那些不被名人堂中的个体所支配的种群中的个体，来更新帕累托前沿名人堂。如果名人堂中的任何个体被支配，则将其移除。

参数:: population – 具有适应度属性的个体列表，用于更新名人堂。

历史¶

class deap.tools.History[源代码]¶

The History 类有助于构建进化过程中产生的所有个体的家谱。它包含两个属性，genealogy_tree 是一个以个体为索引的字典列表，列表包含父母的索引。第二个属性 genealogy_history 包含家谱树中以其个体编号为索引的每个个体。

生成的家谱树与 NetworkX 兼容，以下是如何绘制家谱树

history = History()

# Decorate the variation operators
toolbox.decorate("mate", history.decorator)
toolbox.decorate("mutate", history.decorator)

# Create the population and populate the history
population = toolbox.population(n=POPSIZE)
history.update(population)

# Do the evolution, the decorators will take care of updating the
# history
# [...]

import matplotlib.pyplot as plt
import networkx

graph = networkx.DiGraph(history.genealogy_tree)
graph = graph.reverse()     # Make the graph top-down
colors = [toolbox.evaluate(history.genealogy_history[i])[0] for i in graph]
networkx.draw(graph, node_color=colors)
plt.show()

结合 pygraphviz (dot 布局) 使用 NetworkX，可以从 OneMax 示例中获得这个惊人的家谱树，该示例的种群大小为 20，代数为 5，其中节点的颜色表示其适应度，蓝色表示低，红色表示高。

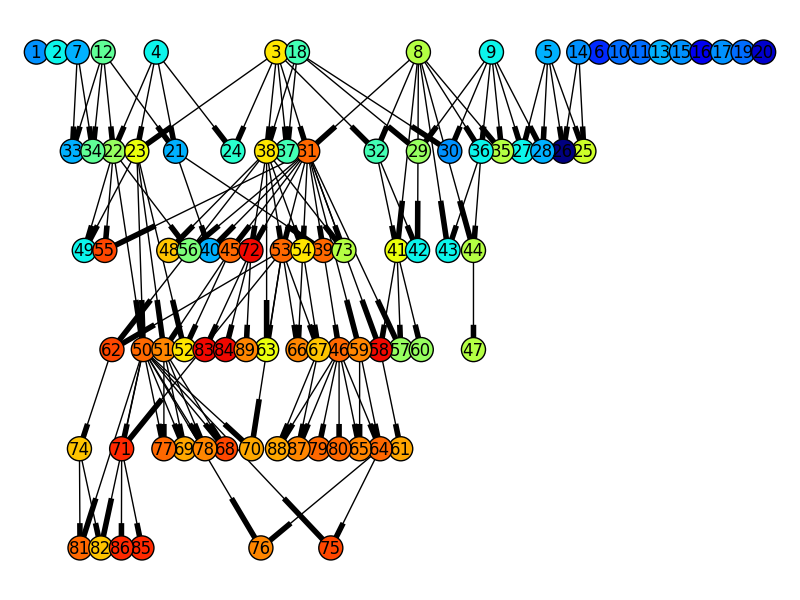
备注

如果你的种群和/或代数很大，家谱树可能会变得非常大。

update(individuals)[源代码]¶

使用新的 individuals 更新历史记录。他们 history_index 属性中的索引将被用来定位他们的父母，然后该索引将被修改为一个唯一的索引，以跟踪这些新个体。此方法应在每次变异后对个体调用。

参数:: individuals – 应插入历史记录的修改人员列表。

如果 individuals 没有 history_index 属性，则添加该属性，并将此个体视为没有父代。此方法应在初始种群上调用以初始化历史记录。

修改历史的内部 genealogy_index 或个人的 history_index 可能会导致不可预测的结果和历史数据的损坏。

decorator¶: 返回一个适当的装饰器以增强工具箱操作符的属性。返回的装饰器假设个体由操作符返回。首先，装饰器调用底层操作，然后使用操作符返回的内容调用 update() 函数。最后，它返回根据更新函数修改了历史参数的个体。

getGenealogy(individual[, max_depth])[源代码]¶

提供一个个体的族谱树。该个体必须有一个属性 history_index，如 update() 所定义，以便检索其关联的族谱树。返回的图包含该个体的父母，最多追溯到 max_depth 代变异之前。如果没有提供最大深度，则追溯到进化开始。

参数:

individual – 家谱树的根节点个体。
max_depth – 根（个体）和叶（父母）之间的大致最大距离，可选。

返回:

一个字典，其中每个键是一个单独的索引，值是对应于父索引的元组。

约束条件¶

class deap.tools.DeltaPenalty(feasibility, delta[, distance])[源代码]¶

这个装饰器为无效个体返回惩罚后的适应度，为有效个体返回原始适应度值。惩罚后的适应度由一个常数因子 delta 加上一个（可选的）*距离* 惩罚组成。如果提供了距离函数，它应返回一个随着个体远离有效区域而增长的值。

参数:

feasibility – 返回任何个体有效性状态的函数。
delta – 返回给无效个体的常量或常量数组。
distance – 返回个体与给定有效点之间距离的函数。距离函数还可以返回一个长度等于目标数量的序列，以不同地影响多目标适应度（可选，默认为0）。

返回:

用于评估函数的装饰器。

此函数依赖于适应度权重来正确添加距离。第 i 个目标的适应度值定义为

\[f^\mathrm{penalty}_i(\mathbf{x}) = \Delta_i - w_i d_i(\mathbf{x})\]

其中 \(\mathbf{x}\) 是个体，\(\Delta_i\) 是用户定义的常数，\(w_i\) 是第 i 个目标的权重。\(\Delta\) 应该比任何可能个体的适应度更差，这意味着对于最小化问题，它高于任何适应度；对于最大化问题，它低于任何适应度。

参见约束处理以获取示例。

class deap.tools.ClosestValidPenalty(feasibility, feasible, alpha[, distance])[源代码]¶

此装饰器为无效个体返回惩罚适应度，为有效个体返回原始适应度值。惩罚适应度由最接近的有效个体的适应度加上加权的（可选的）*距离*惩罚构成。如果提供了距离函数，它应返回一个随着个体远离有效区域而增长的值。

参数:

feasibility – 返回任何个体有效性状态的函数。
feasible – 一个函数，返回从当前无效个体中找到的最接近的可行个体。
alpha – 有效个体与无效个体之间距离的乘法因子。
distance – 返回个体与给定有效点之间距离的函数。距离函数还可以返回一个长度等于目标数量的序列，以不同地影响多目标适应度（可选，默认为0）。

返回:

用于评估函数的装饰器。

此函数依赖于适应度权重来正确添加距离。第 i 个目标的适应度值定义为

\[f^\mathrm{penalty}_i(\mathbf{x}) = f_i(\operatorname{valid}(\mathbf{x})) - \alpha w_i d_i(\operatorname{valid}(\mathbf{x}), \mathbf{x})\]

其中 \(\mathbf{x}\) 是个体，\(\operatorname{valid}(\mathbf{x})\) 是一个返回最接近 \(\mathbf{x}\) 的有效个体的函数，\(\alpha\) 是距离乘法因子，\(w_i\) 是第 i 个目标的权重。

进化工具¶

运算符¶

初始化¶

交叉¶

突变¶

选择¶

Bloat 控制¶

迁移¶

统计¶

日志簿¶

名人堂¶

历史¶

约束条件¶

目录

上一个主题

下一个主题

本页