约束处理¶
进化算法通常是无约束优化过程。在本教程中,我们介绍了几种向进化过程添加不同类型约束的方法。本教程基于Coello Coello的论文 [CoelloCoello2002]。
惩罚函数¶
惩罚函数是处理个体在特定区域内无法评估或因问题特定原因被禁止的最基本方法。惩罚函数根据解决方案中违反约束的程度,给予这些个体适应度上的不利。例如,对于违反约束的个体,可以为其适应度分配一个期望值,而不是进行评估。分配的值可以是常数,也可以随着与有效解决方案距离的增加而增加(对于最大化问题则减少)。下图显示了一个单属性个体的适应度函数 \(g(x)`(绿色)和惩罚函数 :math:`h(x)`(红色),该个体受约束 :math:`3 < x < 7\) 的限制。实线表示实际分配给个体的适应度 \(f(x) = \left\lbrace \begin{array}{cl}g(x) &\mathrm{if}~3 < x < 7\\h(x)&\mathrm{otherwise}\end{array} \right.\)。
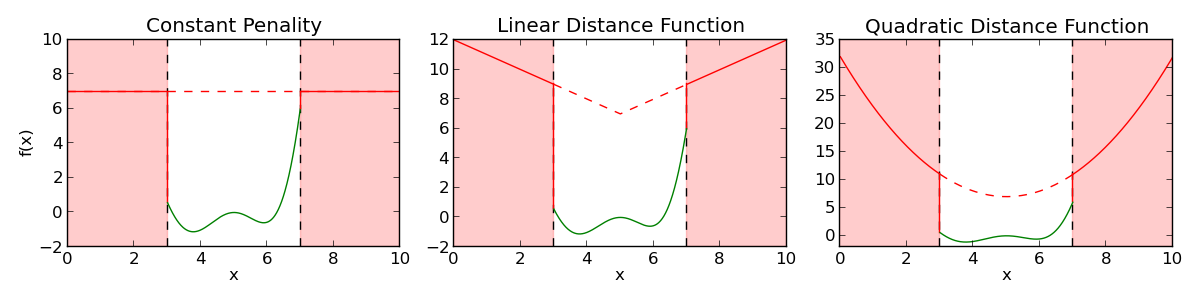
左侧的图在约束不被满足时使用一个恒定的偏移量 \(h(x) = \Delta\)。中间的图除了偏移量外,还使用了欧几里得距离来创建一个类似碗的适应度函数 \(h(x) = \Delta + \sqrt{(x-x_0)^2}\)。最后,右侧的图使用了一个二次距离函数来增加碗的吸引力 \(h(x) = \Delta + (x-x_0)^2\),其中 \(x_0\) 是有效区域的近似中心。
在DEAP中,可以使用 tools 模块中提供的 DeltaPenalty 装饰器将惩罚函数添加到任何评估函数中。:
from math import sin
from deap import base
from deap import tools
def evalFct(individual):
"""Evaluation function for the individual."""
x = individual[0]
return (x - 5)**2 * sin(x) * (x/3),
def feasible(individual):
"""Feasibility function for the individual. Returns True if feasible False
otherwise."""
if 3 < individual[0] < 7:
return True
return False
def distance(individual):
"""A distance function to the feasibility region."""
return (individual[0] - 5.0)**2
toolbox = base.Toolbox()
toolbox.register("evaluate", evalFct)
toolbox.decorate("evaluate", tools.DeltaPenalty(feasible, 7.0, distance))
惩罚装饰器接受两个必需参数和一个可选参数。第一个参数是一个函数,根据用户定义的约束返回个体的有效性。第二个参数是一个常数值(\(\Delta\)),当个体无效时返回。可选参数是一个无效个体与有效区域之间的距离函数。最后一个参数的默认值为0。最后一个示例展示了如何获得顶部图像的右图。
参考文献¶
Coelle Coello, C. A. 进化算法中使用的理论和数值约束处理技术:现状调查. 应用力学和工程中的计算机方法 191, 1245–1287, 2002.