遗传编程¶
要查看某个函数,可以简单地打印出单个候选解决方案以查看其字符串表示。然而,也可以生成一个图形。
遗传编程是进化计算的一个特殊领域,旨在自动构建程序以独立于其领域解决问题。尽管存在多种用于进化程序的表示方法,但最常见的是语法树。
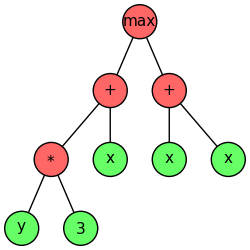
例如,上图展示了程序 \(\max(x + 3 * y, x + x)\)。对于这棵树及后续示例,树的叶子(绿色)称为终端,而内部节点(红色)称为原语。终端分为两种子类型:常量和参数。常量在整个进化过程中保持不变,而参数是程序的输入。对于最后展示的树,参数是变量 \(x\) 和 \(y\),常量是数字 \(3\)。
在DEAP中,用户定义的原语和终端包含在一个原语集中。目前,有两种类型的原语集存在:松散类型和强类型。
松散类型 GP¶
松散类型GP不强制节点之间的特定类型。更具体地说,原语的参数可以是原语集中的任何原语或终端。
以下代码为之前的树定义了一个松散类型的 PrimitiveSet
pset = PrimitiveSet("main", 2)
pset.addPrimitive(max, 2)
pset.addPrimitive(operator.add, 2)
pset.addPrimitive(operator.mul, 2)
pset.addTerminal(3)
第一行创建了一个原始集。它的参数是它将生成的过程的名称("main")及其输入的数量,2。接下来的三行添加了作为原始的函数。第一个参数是要添加的函数,第二个参数是函数的arity。最后一行添加了一个常量终端。目前,参数的默认名称是``”ARG0”和”ARG1”。要将其更改为”x”和”y”``,只需调用:
pset.renameArguments(ARG0="x")
pset.renameArguments(ARG1="y")
在这种情况下,所有函数都接受两个参数。例如,拥有一个接受1个参数的否定函数可以通过以下方式实现::
pset.addPrimitive(operator.neg, 1)
我们的原始集合现在准备好生成一些树了。gp 模块包含了三个前缀表达式生成函数 genFull()、genGrow() 和 genHalfAndHalf()。它们的首个参数是一个原始集合。它们返回一个有效的以列表形式存在的前缀表达式。这个列表的内容可以被 PrimitiveTree 类读取以创建一个前缀树。:
expr = genFull(pset, min_=1, max_=3)
tree = PrimitiveTree(expr)
最后一个代码生成一个有效的高度在1到3之间随机选择的完整树。
强类型 GP¶
在强类型GP中,每个原语和终端都被分配了一个特定的类型。一个原语的输出类型必须与另一个原语的输入类型匹配,以便它们能够连接。例如,如果一个原语返回一个布尔值,那么可以保证这个值不会与一个浮点数相乘,如果乘法运算符仅对浮点数进行操作的话。
def if_then_else(input, output1, output2):
return output1 if input else output2
pset = PrimitiveSetTyped("main", [bool, float], float)
pset.addPrimitive(operator.xor, [bool, bool], bool)
pset.addPrimitive(operator.mul, [float, float], float)
pset.addPrimitive(if_then_else, [bool, float, float], float)
pset.addTerminal(3.0, float)
pset.addTerminal(1, bool)
pset.renameArguments(ARG0="x")
pset.renameArguments(ARG1="y")
在最后一个代码示例中,我们首先定义了一个 if then else 函数,如果第一个参数为真,则返回第二个参数,否则返回第三个参数。然后,我们定义了我们的 PrimitiveSetTyped。同样,该过程被命名为 "main"。第二个参数定义了程序的输入类型。这里,"x" 是一个 bool,而 "y" 是一个 float。第三个参数将程序的输出类型定义为 float。向这个原语集添加原语现在需要设置原语和终端的输入和输出类型。例如,我们首先将 "if_then_else" 函数的第一个参数定义为布尔值,第二个和第三个参数必须是浮点数。该函数被定义为返回一个浮点数。我们现在明白,乘法原语只能有终端 3.0、if_then_else 函数或 "y" 作为输入,这些都是唯一定义的浮点数。
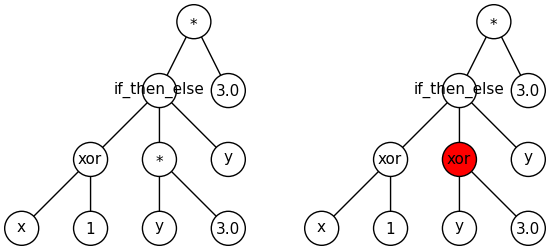
之前的代码可以生成左边的树,但不能生成右边的树,因为类型限制。
备注
树的生成是随机进行的,同时确保类型约束得到遵守。如果任何原语有一个输入类型,没有任何原语和终端可以提供,那么这个原语很可能会被选中并放置在树中,导致在生成器设定的限制内无法完成树的构建。例如,在生成高度为2的完整树时,假设 "op" 接受一个布尔值和一个浮点数, "and" 接受两个布尔值, "neg" 接受一个浮点数,没有定义终端,且参数为布尔值。将会出现以下情况,没有终端可以放置以完成树的构建。
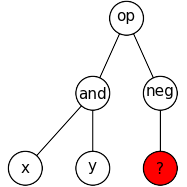
在这种情况下,DEAP 会引发一个 IndexError ,并带有消息 "gp.generate 函数尝试添加一个类型为 float 的终端,但没有可用的终端。"
临时常量¶
一个短暂常量是一个封装了在运行时从给定函数生成的值的终端。短暂常量允许终端不具有所有相同的值。例如,要创建一个在其值在 \([-1, 1)\) 范围内的短暂常量,我们使用
pset.addEphemeralConstant(lambda: random.uniform(-1, 1))
瞬态常量值在其插入树中时确定,除非被另一个瞬态常量替换,否则不会改变。由于它是终端,瞬态常量也可以被类型化。
pset.addEphemeralConstant(lambda: random.randint(-10, 10), int)
生成树个体¶
最后两节中展示的代码生成了有效的树。然而,正如在 运算符和算法 教程中所示,这些树还不是进化的有效个体。必须将创建者和工具箱结合起来才能生成有效的个体。我们需要创建 Fitness 和 Individual 类。除了适应度之外,我们还将原始集的引用添加到 Individual 中。这是由一些 gp 操作符用来修改个体的。:
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMin,
pset=pset)
然后我们将生成函数注册到一个 Toolbox 中。
toolbox = base.Toolbox()
toolbox.register("expr", gp.genFull, pset=pset, min_=1, max_=3)
toolbox.register("individual", tools.initIterate, creator.Individual,
toolbox.expr)
调用 toolbox.individual() 可以方便地返回一个类型为 PrimitiveTree 的个体。
树的评估¶
在 DEAP 中,树可以通过 gp 模块提供的函数转换为可读的 Python 代码并编译为 Python 代码对象。第一个函数 str() 接受一个表达式或 PrimitiveTree,并将其转换为可读的 Python 代码。例如,以下几行代码生成一棵树并输出第一个示例原始集中的代码。
>>> expr = genFull(pset, min_=1, max_=3)
>>> tree = PrimitiveTree(expr)
>>> str(tree)
'mul(add(x, x), max(y, x))'
现在,这个字符串表示我们刚刚生成的程序,但它还不能被执行。为了使其可执行,我们必须将表达式编译成一个Python代码对象。由于这个函数有两个输入,我们希望将代码编译成一个可调用的对象。这可以通过 compile() 实现。该函数有两个参数:要编译的表达式和相关的原语集。以下示例编译了之前的树,并对 \(x=1\) 和 \(y=2\) 的结果函数进行评估。
>>> function = compile(tree, pset)
>>> function(1, 2)
4
当生成的程序没有输入参数时,可以使用相同的 compile() 函数将其编译为字节码。这类问题的一个例子是 人工蚂蚁问题。
树大小限制和膨胀控制¶
由于DEAP使用Python解析器来编译由树表示的代码,因此它继承了其限制。最常见的限制是解析堆栈限制。Python解释器的解析堆栈限制通常固定在92到99之间。这意味着一个表达式最多可以由91个连续的原语组成。换句话说,一棵树的最大深度为91。当超过此限制时,Python会引发以下错误
s_push: parser stack overflow
Traceback (most recent call last):
[...]
MemoryError
由于此限制是在解释器中硬编码的,因此没有简单的方法来增加它。此外,此错误通常源于GP中称为膨胀的现象。也就是说,产生的个体已经达到了一个点,它们包含过多的原语以至于无法有效地解决问题。这个问题导致进化停滞。为了应对这一点,DEAP提供了不同的函数,可以有效地将树的大小和高度限制在可接受的范围内。这些操作符列在 运算符 的GP部分。
绘制树状图¶
函数 deap.gp.graph() 返回使用 NetworX 或 pygraphviz 绘制树图所需的元素。该函数接受一个有效的 PrimitiveTree 对象,并返回一个节点列表、一个边列表和一个将标签与每个节点关联的字典。它可以像下面这样与 pygraphviz 一起使用。
from deap import base, creator, gp
pset = gp.PrimitiveSet("MAIN", 1)
pset.addPrimitive(operator.add, 2)
pset.addPrimitive(operator.sub, 2)
pset.addPrimitive(operator.mul, 2)
pset.renameArguments(ARG0='x')
creator.create("Individual", gp.PrimitiveTree)
toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=2)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
expr = toolbox.individual()
nodes, edges, labels = gp.graph(expr)
### Graphviz Section ###
import pygraphviz as pgv
g = pgv.AGraph()
g.add_nodes_from(nodes)
g.add_edges_from(edges)
g.layout(prog="dot")
for i in nodes:
n = g.get_node(i)
n.attr["label"] = labels[i]
g.draw("tree.pdf")
使用 NetworkX,最后一部分变为:
import matplotlib.pyplot as plt
import networkx as nx
g = nx.Graph()
g.add_nodes_from(nodes)
g.add_edges_from(edges)
pos = nx.graphviz_layout(g, prog="dot")
nx.draw_networkx_nodes(g, pos)
nx.draw_networkx_edges(g, pos)
nx.draw_networkx_labels(g, pos, labels)
plt.show()
根据 graphviz 的版本,节点可能会以不可预测的顺序出现。同一棵树的两个图可能会有兄弟节点交换位置。这不会影响原始树的表示形式,也不会影响数值结果。
如何进化程序¶
进化程序树的不同方法通过 遗传编程 (GP) 示例展示。