阿特拉斯

包含最多6个节点的所有连通图的图集。

此示例通过PyGraphviz使用Graphviz。

图像应显示142个图。 我们不绘制空图和单节点图。 （142是序列oeis.org/A001349中从2到n=6的值的总和）。

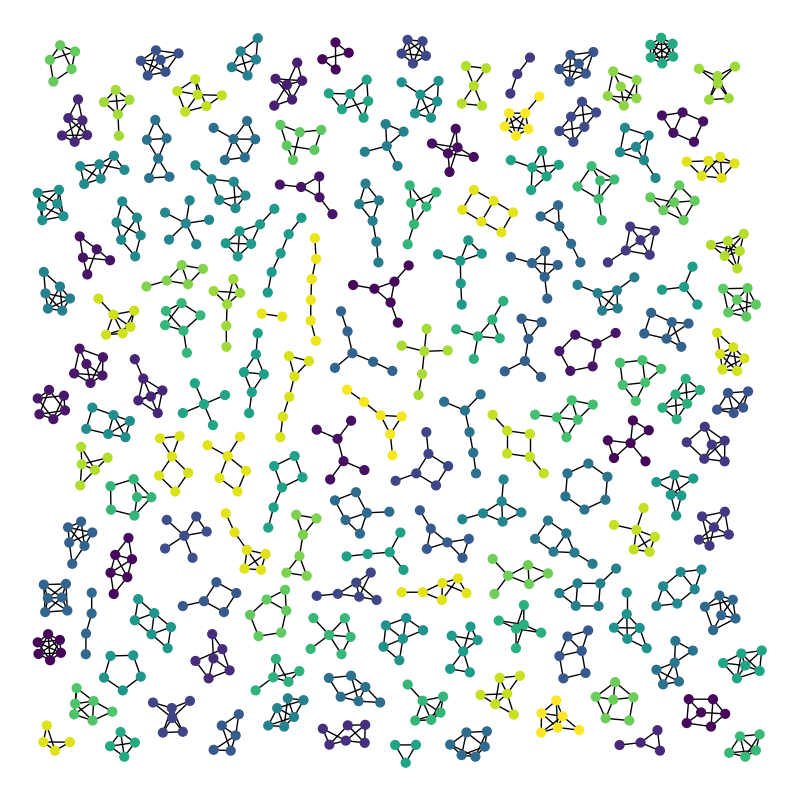
Graph named 'G208' with 809 nodes and 1112 edges
142 connected components

import random

import matplotlib.pyplot as plt
import networkx as nx


GraphMatcher = nx.isomorphism.vf2userfunc.GraphMatcher


def atlas6():
    """返回所有最多包含6个节点的连通图的图集"""

    Atlas = nx.graph_atlas_g()[3:209]  # 0, 1, 2 => 无边。208 是最后一个 6 节点图
    U = nx.Graph()  # 图集内所有图的并集图
    for G in Atlas:
        # 检查是否已连接
        if nx.number_connected_components(G) == 1:
            # 检查是否与之前的图同构
            if not GraphMatcher(U, G).subgraph_is_isomorphic():
                U = nx.disjoint_union(U, G)
    return U


G = atlas6()

print(G)
print(nx.number_connected_components(G), "connected components")

plt.figure(1, figsize=(8, 8))
# 使用graphviz neato布局图表并设置位置
pos = nx.nx_agraph.graphviz_layout(G, prog="neato")
# 在每个连通子图中将节点颜色保持一致
C = (G.subgraph(c) for c in nx.connected_components(G))
for g in C:
    c = [random.random()] * nx.number_of_nodes(g)  # 随机颜色...
    nx.draw(g, pos, node_size=40, node_color=c, vmin=0.0, vmax=1.0, with_labels=False)
plt.show()