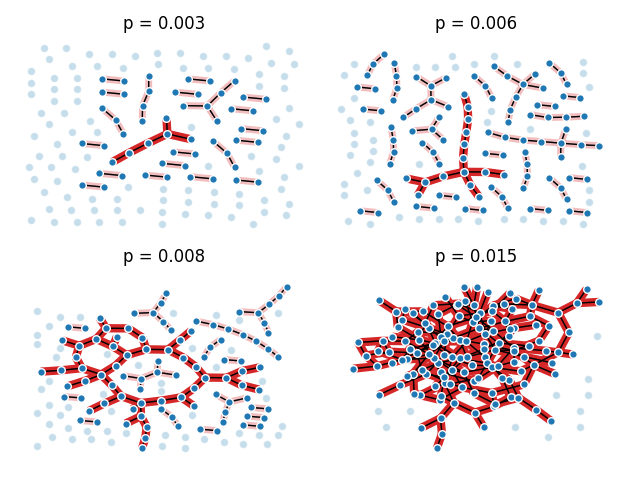
巨型组件

此示例展示了在二项式随机图中巨型连通组件的突然出现。

此示例需要 Graphviz 和 PyGraphviz。

import math

import matplotlib.pyplot as plt
import networkx as nx

n = 150  # 150个节点
# 预期出现巨型组件（大小为log(n)个节点）的p值
p_giant = 1.0 / (n - 1)
# 图中预期完全连通的p值
p_conn = math.log(n) / n

# 以下p值范围应接近阈值
pvals = [0.003, 0.006, 0.008, 0.015]

fig, axes = plt.subplots(2, 2)
for p, ax, seed in zip(pvals, axes.ravel(), range(len(pvals))):
    #### 生成图表 ####
    G = nx.binomial_graph(n, p, seed=seed)
    # 识别连接/断开的节点
    connected = [n for n, d in G.degree() if d > 0]
    disconnected = list(set(G.nodes()) - set(connected))
    # 识别最大的连通分量
    Gcc = sorted(nx.connected_components(G), key=len, reverse=True)
    G0 = G.subgraph(Gcc[0])
    #### 绘制图表 ####
    pos = nx.nx_agraph.graphviz_layout(G)
    ax.set_title(f"p = {p:.3f}")
    # 绘制最大的连通分量
    options = {"ax": ax, "edge_color": "tab:red"}
    nx.draw_networkx_edges(G0, pos, width=6.0, **options)
    # 绘制其他连接的组件
    for Gi in Gcc[1:]:
        if len(Gi) > 1:
            nx.draw_networkx_edges(G.subgraph(Gi), pos, alpha=0.3, width=5.0, **options)
    # 绘制连接/断开连接的节点
    options = {"ax": ax, "node_size": 30, "edgecolors": "white"}
    nx.draw(G, pos, nodelist=connected, **options)
    nx.draw(G, pos, nodelist=disconnected, alpha=0.25, **options)
fig.tight_layout()
plt.show()