一个混合问题

问题描述

Whiskas 猫粮，如上所示，由 Uncle Ben’s 生产。Uncle Ben’s 希望在确保满足罐头上标明的营养分析要求的同时，尽可能廉价地生产他们的猫粮产品。因此，他们希望在仍然满足其营养标准的情况下，改变每种成分的使用量（主要成分包括鸡肉、牛肉、羊肉、大米、小麦和明胶）。

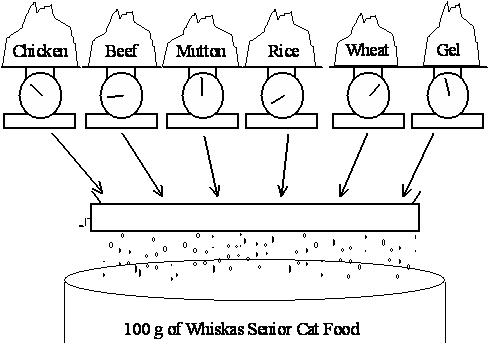
鸡肉、牛肉和羊肉的成本分别为 $0.013、$0.008 和 $0.010，而大米、小麦和凝胶的成本分别为 $0.002、$0.005 和 $0.001。（所有成本均为每克。）在本练习中，我们将忽略维生素和矿物质成分。（无论如何，这些成分的成本可能都非常小。）

每种成分都对最终产品的蛋白质、脂肪、纤维和盐的总重量有贡献。每克成分的贡献（以克为单位）在下表中给出。

东西	蛋白质	胖	纤维	盐
鸡	0.100	0.080	0.001	0.002
牛肉	0.200	0.100	0.005	0.005
羊肉	0.150	0.110	0.003	0.007
米饭	0.000	0.010	0.100	0.002
小麦麸皮	0.040	0.010	0.150	0.008
凝胶	0.000	0.000	0.000	0.000

简化公式

首先，我们将考虑一个简化的问题来构建一个简单的Python模型。

确定决策变量

假设 Whiskas 想要用两种成分来制作他们的猫粮：鸡肉和牛肉。我们首先定义我们的决策变量：

\[\begin{split}x_1 &= ext{ 罐头猫粮中鸡肉的百分比 }\\ x_2 &= ext{ 罐头猫粮中牛肉的百分比 }\end{split}\]

这些变量的限制（大于零）必须注意，但对于Python实现，它们不会单独输入或与其他约束一起列出。

制定目标函数

目标函数变为：

\[\textbf{ 最小化 } 0.013 x_1 + 0.008 x_2\]

约束条件

变量的约束条件是它们必须总和为100，并且满足营养需求：

\[\begin{split}1.000 x_1 + 1.000 x_2 &= 100.0\\ 0.100 x_1 + 0.200 x_2 &\ge 8.0\\ 0.080 x_1 + 0.100 x_2 &\ge 6.0\\ 0.001 x_1 + 0.005 x_2 &\le 2.0\\ 0.002 x_1 + 0.005 x_2 &\le 0.4\\\end{split}\]

简化问题的解决方案

要获得这个线性规划的解，我们可以编写一个简短的Python程序来调用PuLP的建模函数，然后调用求解器。这将一步一步地解释如何编写这个Python程序。建议你自己重复这个练习。这个示例的代码可以在 WhiskasModel1.py 中找到。

文件的开头应包含一个简短的注释部分，概述程序的目的。例如：

"""
The Simplified Whiskas Model Python Formulation for the PuLP Modeller

Authors: Antony Phillips, Dr Stuart Mitchell  2007
"""

然后你将导入 PuLP 的函数以便在你的代码中使用：

# Import PuLP modeler functions
from pulp import *

使用 LpProblem 函数创建了一个名为 prob 的变量（尽管其名称并不重要）。它有两个参数，第一个是此问题的任意名称（作为字符串），第二个参数根据您试图解决的 LP 类型，可以是 LpMinimize 或 LpMaximize：

# Create the 'prob' variable to contain the problem data
prob = LpProblem("The Whiskas Problem", LpMinimize)

问题变量 x1 和 x2 是通过 LpVariable 类创建的。它有四个参数，第一个是此变量所代表的任意名称，第二个是此变量的下限，第三个是上限，第四个是数据类型（离散或连续）。第四个参数的选项是 LpContinuous 或 LpInteger，默认值为 LpContinuous。如果我们正在建模要生产的罐数，我们需要输入 LpInteger，因为它是离散数据。界限可以直接输入为数字，或者 None 表示无界限（即正或负无穷大），默认值为 None。如果输入了前几个参数而其余的被忽略（如所示），它们将采用默认值。但是，如果你想指定第三个参数，但希望第二个参数为默认值，你需要将第二个参数明确设置为其默认值。即你不能留下参数条目空白。例如:

LpVariable("example", None, 100)

或者:

LpVariable("example", upBound = 100)

要显式创建此问题所需的两个变量：

# The 2 variables Beef and Chicken are created with a lower limit of zero
x1 = LpVariable("ChickenPercent", 0, None, LpInteger)
x2 = LpVariable("BeefPercent", 0)

变量 prob 现在开始使用 += 运算符收集问题数据。目标函数首先被逻辑地输入，在语句末尾有一个重要的逗号 , ，以及一个简短的字符串解释这个目标函数是什么：

# The objective function is added to 'prob' first
prob += 0.013 * x1 + 0.008 * x2, "Total Cost of Ingredients per can"

现在输入约束条件（注意：任何“非负”约束在定义变量时已经包含）。这是通过再次使用 ‘+=’ 运算符完成的，因为我们正在向 prob 变量添加更多数据。约束条件在此之后逻辑上输入，约束方程末尾有一个逗号，并简要描述该约束的原因：

# The five constraints are entered
prob += x1 + x2 == 100, "PercentagesSum"
prob += 0.100 * x1 + 0.200 * x2 >= 8.0, "ProteinRequirement"
prob += 0.080 * x1 + 0.100 * x2 >= 6.0, "FatRequirement"
prob += 0.001 * x1 + 0.005 * x2 <= 2.0, "FibreRequirement"
prob += 0.002 * x1 + 0.005 * x2 <= 0.4, "SaltRequirement"

现在所有的问题数据都已输入，可以使用 writeLP() 函数将这些信息复制到代码块运行目录中的 .lp 文件中。一旦代码成功运行，你可以用文本编辑器打开这个 .lp 文件，查看上述步骤在做什么。你会注意到这一行没有赋值操作符（如等号）。这是因为 writeLP() 函数/方法正在对变量/对象 prob 执行（并且字符串 "WhiskasModel.lp" 是一个附加参数）。变量/对象和函数/方法之间的点 . 很重要，并且在面向对象的软件中经常看到（如本例）：

# The problem data is written to an .lp file
prob.writeLP("WhiskasModel.lp")

LP 问题使用 PuLP 选择的求解器来解决。在这种情况下，solve() 后的输入括号是空的，但它们可以用来指定使用哪个求解器（例如 prob.solve(CPLEX()) ）：

# The problem is solved using PuLP's choice of Solver
prob.solve()

Now the results of the solver call can be displayed as output to us. Firstly, we request the status of the solution, which can be one of “Not Solved”, “Infeasible”, “Unbounded”, “Undefined” or “Optimal”. The value of prob (pulp.pulp.LpProblem.status) is returned as an integer, which must be converted to its significant text meaning using the LpStatus dictionary. Since LpStatus is a dictionary(dict), its input must be in square brackets:

# The status of the solution is printed to the screen
print("Status:", LpStatus[prob.status])

现在可以将变量及其解析后的最优值打印到屏幕上。

# Each of the variables is printed with it's resolved optimum value
for v in prob.variables():
    print(v.name, "=", v.varValue)

for 循环使 variable 遍历所有问题变量名称（在此例中仅为 ChickenPercent 和 BeefPercent）。然后它打印每个变量名称，后跟一个等号，再后跟其最优值。name 和 varValue 是对象 variable 的属性。

优化后的目标函数值会打印到屏幕上，使用值函数。这确保了数字以正确的格式显示。objective 是对象 prob 的一个属性：

# The optimised objective function value is printed to the screen
print("Total Cost of Ingredients per can = ", value(prob.objective))

运行此文件应生成输出，显示鸡肉将占33.33%，牛肉将占66.67%，每罐配料的总成本为96美分。

完整公式

现在我们将用所有变量全面表述问题。虽然它可以简单地通过上述方法实现到Python中，但我们将探讨一种更好的方法，这种方法不会过多地将问题数据和表述混合在一起。这将使更改任何问题数据以进行其他测试变得更加容易。我们将以代数方式定义问题，从同样的方式开始：

1. 确定Whiskas猫粮问题的决策变量，决策变量是我们包含在罐头中不同成分的百分比。由于罐头是100克，这些百分比也代表每种成分包含的克数。我们必须正式定义我们的决策变量，确保说明我们使用的单位。

   \[\begin{split}x_1 &= \text{罐头猫粮中鸡肉的百分比}\\ x_2 &= \text{罐头猫粮中牛肉的百分比}\\ x_3 &= \text{罐头猫粮中羊肉的百分比}\\ x_4 &= \text{罐头猫粮中米的百分比}\\ x_5 &= \text{罐头猫粮中麦麸的百分比}\\ x_6 &= \text{罐头猫粮中凝胶的百分比}\end{split}\]

   请注意，这些百分比必须在0到100之间。

2. 为Whiskas猫粮问题制定目标函数，目标是使每罐猫粮的原料总成本最小化。我们知道每克每种原料的成本。我们决定每种原料在罐中的百分比，因此我们必须除以100并乘以罐的重量（克）。这将给我们每种原料的重量（克）：

   \[ \begin{align}\begin{aligned}\min \$0.013 x_1 + \$0.008 x_2 + \$0.010 x_3 + \$0.002 x_4 + \$0.005 x_5 + \$0.001 x_6\\最小化 \$0.013 x_1 + \$0.008 x_2 + \$0.010 x_3 + \$0.002 x_4 + \$0.005 x_5 + \$0.001 x_6\end{aligned}\end{align} \]

3. 制定约束条件 Whiskas 猫粮问题的约束条件是：

   • 百分比的总和必须构成整个罐（= 100%）。

   • 所述的营养分析要求已满足。

   “整个罐子”的约束是：

   \[x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 100\]

   为了满足营养分析的要求，我们需要每100克至少含有8克蛋白质，6克脂肪，但纤维不超过2克，盐不超过0.4克。为了制定这些约束条件，我们利用了之前每个成分贡献的表格。这使我们能够对成分中蛋白质、脂肪、纤维和盐的总贡献制定以下约束条件：

   \[\begin{split}0.100 x_1 +0.200 x_2 +0.150 x_3 +0.000 x_4 +0.040 x_5 +0.0 x_6 0&\ge 8.0 \\ 0.080 x_1 +0.100 x_2 +0.110 x_3 +0.010 x_4 +0.010 x_5 0+0.0 x_6 &\ge 6.0 \\ 0.001 x_1 +0.005 x_2 +0.003 x_3 +0.100 x_4 0+0.150 x_5 +0.0 x_6 &\le 2.0 \\ 0.002 x_1 +0.005 x_2 +0.007 x_3 0+0.002 x_4 +0.008 x_5 +0.0 x_6 &\le 0.4\end{split}\]

完整问题的解决方案

要获得这个线性规划的解，我们再次编写一个简短的Python程序来调用PuLP的建模函数，这些函数随后会调用一个求解器。这将一步一步地解释如何编写这个Python程序及其对上述模型的改进。建议你自己重复这个练习。这个例子的代码可以在 WhiskasModel2.py 中找到。

与上次一样，建议在文件开头注明其目的、作者姓名和日期。导入 PuLP 函数的方式也相同：

"""
The Full Whiskas Model Python Formulation for the PuLP Modeller

Authors: Antony Phillips, Dr Stuart Mitchell  2007
"""

# Import PuLP modeler functions
from pulp import *

接下来，在定义 prob 变量或问题类型之前，关键的问题数据被输入到字典中。这包括原料列表，随后是每种原料的成本，以及每种原料中四种营养成分的百分比。这些值清晰地列出，并且可以很容易地被编程知识较少的人更改。原料是参考键，数字是数据。

# Creates a list of the Ingredients
Ingredients = ["CHICKEN", "BEEF", "MUTTON", "RICE", "WHEAT", "GEL"]

# A dictionary of the costs of each of the Ingredients is created
costs = {
    "CHICKEN": 0.013,
    "BEEF": 0.008,
    "MUTTON": 0.010,
    "RICE": 0.002,
    "WHEAT": 0.005,
    "GEL": 0.001,
}

# A dictionary of the protein percent in each of the Ingredients is created
proteinPercent = {
    "CHICKEN": 0.100,
    "BEEF": 0.200,
    "MUTTON": 0.150,
    "RICE": 0.000,
    "WHEAT": 0.040,
    "GEL": 0.000,
}

# A dictionary of the fat percent in each of the Ingredients is created
fatPercent = {
    "CHICKEN": 0.080,
    "BEEF": 0.100,
    "MUTTON": 0.110,
    "RICE": 0.010,
    "WHEAT": 0.010,
    "GEL": 0.000,
}

# A dictionary of the fibre percent in each of the Ingredients is created
fibrePercent = {
    "CHICKEN": 0.001,
    "BEEF": 0.005,
    "MUTTON": 0.003,
    "RICE": 0.100,
    "WHEAT": 0.150,
    "GEL": 0.000,
}

# A dictionary of the salt percent in each of the Ingredients is created
saltPercent = {
    "CHICKEN": 0.002,
    "BEEF": 0.005,
    "MUTTON": 0.007,
    "RICE": 0.002,
    "WHEAT": 0.008,
    "GEL": 0.000,
}

prob 变量被创建来包含公式，并且通常的参数被传递给 LpProblem。

# Create the 'prob' variable to contain the problem data
prob = LpProblem("The Whiskas Problem", LpMinimize)

创建了一个名为 ingredient_vars 的字典，其中包含 LP 变量，其定义的下限为零。字典的引用键是原料名称，数据是 Ingr_IngredientName。（例如：MUTTON: Ingr_MUTTON）

# A dictionary called 'ingredient_vars' is created to contain the referenced Variables
ingredient_vars = LpVariable.dicts("Ingr", Ingredients, 0)

由于 costs 和 ingredient_vars 现在是字典，其引用键为原料名称，因此可以通过列表推导简单地提取数据，如所示。lpSum() 函数将添加结果列表的元素。因此，目标函数可以简单地输入并分配一个名称：

# The objective function is added to 'prob' first
prob += (
    lpSum([costs[i] * ingredient_vars[i] for i in Ingredients]),
    "Total Cost of Ingredients per can",
)

进一步使用列表推导式来定义其他5个约束条件，这些约束条件也各自被赋予了描述性的名称。

# The five constraints are added to 'prob'
prob += lpSum([ingredient_vars[i] for i in Ingredients]) == 100, "PercentagesSum"
prob += (
    lpSum([proteinPercent[i] * ingredient_vars[i] for i in Ingredients]) >= 8.0,
    "ProteinRequirement",
)
prob += (
    lpSum([fatPercent[i] * ingredient_vars[i] for i in Ingredients]) >= 6.0,
    "FatRequirement",
)
prob += (
    lpSum([fibrePercent[i] * ingredient_vars[i] for i in Ingredients]) <= 2.0,
    "FibreRequirement",
)
prob += (
    lpSum([saltPercent[i] * ingredient_vars[i] for i in Ingredients]) <= 0.4,
    "SaltRequirement",
)

在此之后，writeLP() 行等与简化示例中的完全相同。

最佳解决方案是60%的牛肉和40%的明胶，导致目标函数值为每罐52美分。