运输问题
问题描述
一家精品酿酒厂有两个仓库,从这两个仓库向五家精心挑选的酒吧分销啤酒。每周初,每家酒吧都会向酿酒厂总部发送啤酒订单,然后从相应的仓库向酒吧发货。酿酒厂希望有一个互动的计算机程序,他们可以每周运行一次,告诉他们哪个仓库应该供应哪个酒吧,以最小化整个运营的成本。例如,假设在某个星期的开始,仓库A有1000箱,仓库B有4000箱,而酒吧分别需要500、900、1800、200和700箱。哪个仓库应该供应哪个酒吧?
配方
对于运输问题,在制定问题时使用问题的图形表示通常是有帮助的。以下是啤酒配送问题的图形表示。
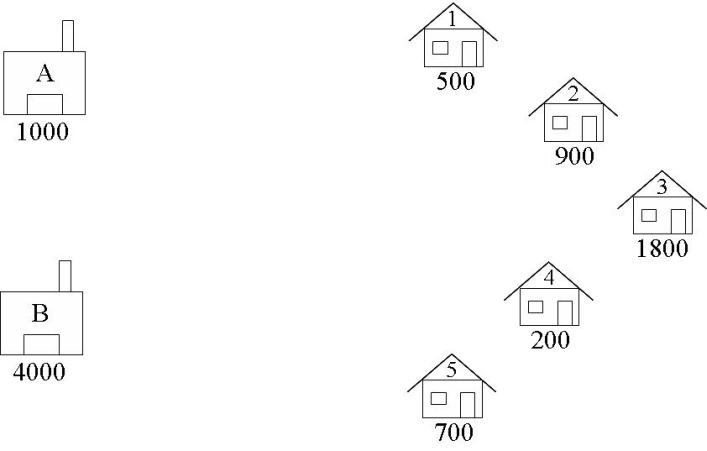
识别决策变量
在运输问题中,我们决定如何将货物从供应节点运输到需求节点。决策变量是连接这些节点的弧,如下图所示。我们决定从每个仓库向每个酒吧运输多少箱啤酒。
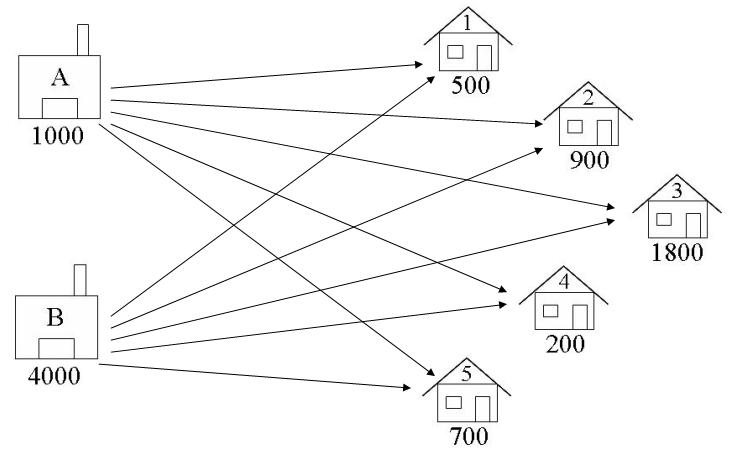
A1 = 从仓库A运送到酒吧1的啤酒箱数
A5 = 从仓库A运送到酒吧5的啤酒箱数
B1 = 从仓库 B 运送到酒吧 1 的啤酒箱数
B5 = 从仓库 B 运送到酒吧 5 的啤酒箱数
设:
变量的下限为零,且所有值必须为整数(因为箱子的数量不能为负数或分数)。没有上限。
制定目标函数
目标函数已被松散地定义为成本。只有当从仓库到酒吧的运输成本是运输箱子数量的线性函数时,问题才能被表述为一个线性规划问题。请注意,情况并非总是如此。这可能是由于规模经济或固定成本等因素。例如,运输10个箱子的成本可能不会是运输1个箱子成本的10倍,因为一辆卡车可能同样容易地容纳1个或10个箱子。通常在这种情况下,运营卡车的固定成本意味着成本会跳跃式上升(当需要额外的卡车时)。在这些情况下,可以通过使用零一整数变量来建模此类成本:我们将在课程的后面部分对此进行探讨。
我们假设每个箱子有一个固定的运输成本。(如果卡车的容量相对于必须交付的箱子数量很小,那么这是一个有效的假设)。让我们假设我们与财务经理交谈,她给了我们以下运输成本(每箱美元):
从仓库到酒吧
A
B
toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。2
3
2
4
toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。3
5
3
4
2
2
5
toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。3
- 最小化运输成本 = 路线A1的每箱成本 * A1(路线A1上的箱数)
+ … + RouteB5 每箱成本 * B5(RouteB5 上的箱数)
制定约束条件
约束来自于供需的考虑。仓库A的啤酒供应量为1000箱。从仓库A运出的啤酒总量不能超过这个数量。同样,从仓库B运出的啤酒量不能超过仓库B的啤酒供应量。从仓库出发的所有弧上的值的总和,必须小于或等于该仓库的供应值:
使得:
A1 + A2 + A3 + A4 + A5 <= 1000
B1 + B2 + B3 + B4 + B5 <= 4000
酒吧1对啤酒的需求是500箱,因此运送到那里的啤酒量必须至少为500箱,以避免销售损失。同样,考虑到运送到其他酒吧的啤酒量必须至少等于这些酒吧的需求。注意,我们假设超额供应酒吧没有惩罚(除了我们产生的额外运输成本)。我们可以_平衡_运输问题,以确保需求完全满足——稍后会有更多关于这方面的内容。目前,所有指向一个酒吧的弧上的值的总和必须大于或等于该酒吧的需求值:
A1 + B1 >= 500
A2 + B2 >= 900
A3 + B3 >= 1800
A4 + B4 >= 200
A5 + B5 >= 700
最后,我们已经规定了运送的啤酒数量必须为非负数。
PuLP 模型
虽然如上定义的LP可以以与 A Blending Problem (Whiskas) 相同的方式转换为Python代码,但对于运输问题,有一种更有效的方法,我们将在本课程中使用。此问题的示例文件可以在示例目录中找到,名为 BeerDistributionProblem.py
首先,从标题和导入 PuLP 语句开始你的 Python 文件:
"""
The Beer Distribution Problem for the PuLP Modeller
Authors: Antony Phillips, Dr Stuart Mitchell 2007
"""
# Import PuLP modeler functions
from pulp import *
公式的开始是对节点及其限制/容量的简单定义。节点名称被放入列表中,而它们的相关容量则被放入以节点名称为引用键的字典中:
# Creates a list of all the supply nodes
Warehouses = ["A", "B"]
# Creates a dictionary for the number of units of supply for each supply node
supply = {"A": 1000, "B": 4000}
# Creates a list of all demand nodes
Bars = ["1", "2", "3", "4", "5"]
# Creates a dictionary for the number of units of demand for each demand node
demand = {
"1": 500,
"2": 900,
"3": 1800,
"4": 200,
"5": 700,
}
成本数据随后被输入到一个列表中,该列表包含两个子列表:第一个子列表包含从仓库A发货的成本,第二个子列表包含从仓库B发货的成本。请注意,代码的注释和结构使得数据呈现为表格形式,便于编辑。Warehouses 和 Bars 列表(供应和需求节点)被添加以形成一个大型列表(所有节点),并输入到PuLP的`makeDict`函数中。第二个参数是之前创建的成本列表,最后一个参数设置弧成本的默认值。一旦创建了成本字典,如果调用 costs[“A”][“1”],它将返回从仓库A运送到酒吧1的成本,2。如果调用 costs[“C”][“2”],它将返回0,因为这是定义的默认值。
# Creates a list of costs of each transportation path
costs = [ # Bars
# 1 2 3 4 5
[2, 4, 5, 2, 1], # A Warehouses
[3, 1, 3, 2, 3], # B
]
# The cost data is made into a dictionary
costs = makeDict([Warehouses, Bars], costs, 0)
prob 变量是使用 LpProblem 函数创建的,带有通常的输入参数。
# Creates the 'prob' variable to contain the problem data
prob = LpProblem("Beer Distribution Problem", LpMinimize)
创建一个包含所有弧的元组列表。
# Creates a list of tuples containing all the possible routes for transport
Routes = [(w, b) for w in Warehouses for b in Bars]
创建了一个名为 vars 的字典,其中包含 LP 变量。字典的引用键是仓库名称,然后是酒吧名称([“A”][“2”]),数据是 Route_Tuple。(例如 [“A”][“2”]:Route_A_2)。设置了下限为零,上限为 None,并且变量被定义为整数。
# A dictionary called 'Vars' is created to contain the referenced variables(the routes)
vars = LpVariable.dicts("Route", (Warehouses, Bars), 0, None, LpInteger)
目标函数通过列表推导式添加到变量 prob 中。由于 vars 和 costs 现在是字典(包含更深层的字典),它们可以像表格一样使用,因为 for (w,b) in Routes 将遍历所有组合/弧。注意,虽然可以使用 i 和 j,但 w 和 b 更具意义。
# The objective function is added to 'prob' first
prob += (
lpSum([vars[w][b] * costs[w][b] for (w, b) in Routes]),
"Sum_of_Transporting_Costs",
)
供需约束是通过一个普通的 for 循环和一个列表推导式添加的。供应约束:对于每个仓库,依次将决策变量(弧上的啤酒箱数)的值求和,然后约束其小于或等于该仓库的供应上限。需求约束:对于每个酒吧,依次将决策变量(弧上的数量)的值从每个仓库求和,然后约束其大于或等于需求下限。
# The supply maximum constraints are added to prob for each supply node (warehouse)
for w in Warehouses:
prob += (
lpSum([vars[w][b] for b in Bars]) <= supply[w],
f"Sum_of_Products_out_of_Warehouse_{w}",
)
# The demand minimum constraints are added to prob for each demand node (bar)
for b in Bars:
prob += (
lpSum([vars[w][b] for w in Warehouses]) >= demand[b],
f"Sum_of_Products_into_Bar{b}",
)
接下来是 prob.writeLP 行,其余部分如前例所述。
这个示例的代码可以在 BeerDistributionProblem.py 中找到。
你会注意到线性规划的解也是一个整数解。只要供应和需求是整数,线性规划的解总是整数。阅读关于自然整数解的更多细节。
扩展
验证
由于我们已经保证了供需是整数,我们知道线性规划的解将是整数,因此我们不需要检查解的整数性。
存储和“买入”
交通模型通常是 _平衡的_,即总供给 = 总需求。这是因为额外的供给通常必须存储在某个地方(伴随着存储成本),而额外的需求通常通过从替代来源购买额外商品(这被称为“购买”额外商品)或通过替代另一种产品(产生惩罚成本)来满足。
在啤酒分销问题中,总供应量为5000箱啤酒,但总需求仅为4100箱。多余的供应可以发送到一个_虚拟_需求节点。流向虚拟需求节点的流量成本即为每个供应节点的存储成本。
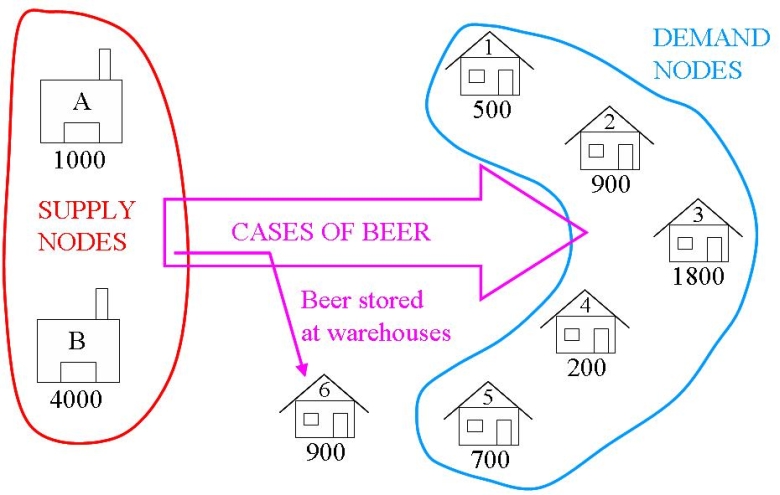
这非常简单地添加到上述模型中。由于目标函数和约束条件都作用于原始的供应、需求和成本列表/字典,因此要包含另一个需求节点,唯一需要做的更改是:
# Creates a dictionary for the number of units of supply for each supply node
supply = {"A": 1000, "B": 4000}
# Creates a list of all demand nodes
Bars = ["1", "2", "3", "4", "5", "D"]
# Creates a dictionary for the number of units of demand for each demand node
demand = {"1": 500, "2": 900, "3": 1800, "4": 200, "5": 700, "D": 900}
# Creates a list of costs of each transportation path
costs = [ # Bars
# 1 2 3 4 5 D
[2, 4, 5, 2, 1, 0], # A Warehouses
[3, 1, 3, 2, 3, 0], # B
]
Bars 列表被展开,Demand 字典也被展开,以使 Dummy Demand 需要 900 个箱子,从而平衡问题。成本列表也被展开,以显示“发送至 Dummy Node”的成本,这在现实中只是将库存留在仓库中。这可能会有相关成本,可以在这里输入,而不是零。请注意,即使供应过剩不平衡,解决方案仍然可以解决。
如果一个运输问题需求大于供应,我们可以通过使用一个虚拟供应节点来平衡问题。注意,在需求过剩的情况下,问题在未平衡时是“不可行的”。
假设出现了一个生产问题,只能生产4000箱啤酒。由于总需求是4100箱,我们需要从虚拟供应节点获取额外的啤酒箱。
这个示例的代码可以在 BeerDistributionProblemWarehouseExtension.py 中找到。
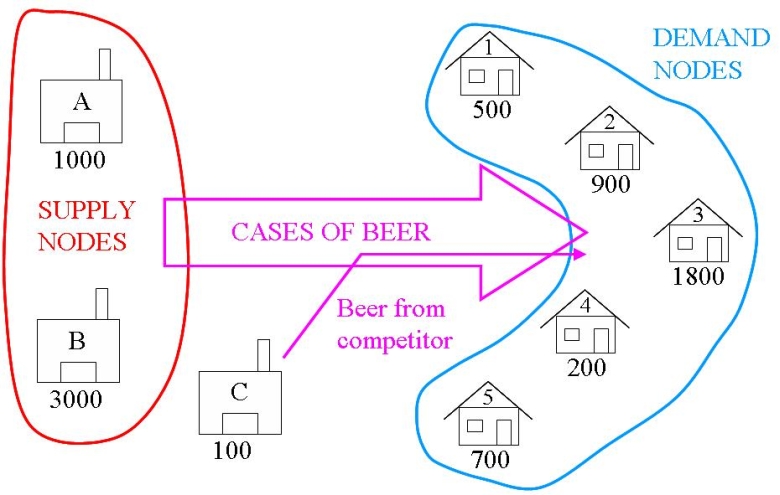
这个虚拟供应节点简单且逻辑上被添加到 Warehouse 列表、Supply 字典和 costs 列表中。供应值被选择来平衡问题,并且运输成本对所有需求节点为零。
# Creates a list of all the supply nodes
Warehouses = ["A", "B", "C"]
# Creates a dictionary for the number of units of supply for each supply node
supply = {"A": 1000, "B": 4000, "C": 100}
# Creates a list of all demand nodes
Bars = ["1", "2", "3", "4", "5"]
# Creates a dictionary for the number of units of demand for each demand node
demand = {
"1": 500,
"2": 900,
"3": 1800,
"4": 200,
"5": 700,
}
# Creates a list of costs of each transportation path
costs = [ # Bars
# 1 2 3 4 5
[2, 4, 5, 2, 1], # A Warehouses
[3, 1, 3, 2, 3], # B
[0, 0, 0, 0, 0],
]
此示例的代码可以在 BeerDistributionProblemCompetitorExtension.py 中找到。
解决方案和分析的展示
有许多方式来展示啤酒配送问题的解决方案:如配送清单、表格等。
TRANSPORTATION SOLUTION -- Non-zero shipments
TotalCost = ____
Ship ___ crates of beer from warehouse A to pub 1
Ship ___ crates of beer from warehouse A to pub 5
Ship ___ crates of beer from warehouse B to pub 1
Ship ___ crates of beer from warehouse B to pub 2
Ship ___ crates of beer from warehouse B to pub 3
Ship ___ crates of beer from warehouse B to pub 4
这些信息产生了以下管理摘要:
The Beer Distribution Problem
Mike O'Sullivan, 1234567
We are minimising the transportation cost for a brewery operation. The brewery
transports cases of beer from its warehouses to several bars.
The brewery has two warehouses (A and B respectively) and 5 bars (1, 2, 3, 4 and
5).
The supply of crates of beer at the warehouses is:
__________
The forecasted demand (in crates of beer) at the bars is:
__________
The cost of transporting 1 crate of beer from a warehouse to a bar is given in
the following table:
__________
To minimise the transportation cost the brewery should make the following
shipments:
Ship ___ crates of beer from warehouse A to pub 1
Ship ___ crates of beer from warehouse A to pub 5
Ship ___ crates of beer from warehouse B to pub 1
Ship ___ crates of beer from warehouse B to pub 2
Ship ___ crates of beer from warehouse B to pub 3
Ship ___ crates of beer from warehouse B to pub 4
The total transportation cost of this shipping schedule is $_____.
持续监控
持续监控可以采取以下形式:
更新您的数据文件并在数据变化时进行解析(成本、供应、需求的变化);
解析我们模型中的新节点(例如,新仓库或酒吧);
寻找在运输成本影响最优解的路线上是否有更便宜的运输选项(例如,通过减少从仓库B到酒吧1的运输成本,我们可以获得多少总节省)。