一个作为LP形式化的数独问题
问题描述
一个 数独问题 是一个包含不完整9x9数字表格的问题,必须根据几条规则进行填充:
在任何一个 3x3 的方格内,数字 1 到 9 都必须出现。
在9x9网格的任何一列中,必须找到从1到9的每个数字。
在9x9网格的任何一行中,必须找到数字1到9中的每一个。
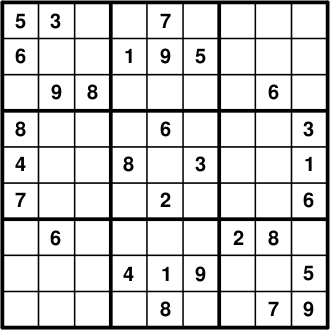
在本页中,我们将使用 PuLP 将以下(来自维基百科)的问题制定为一个模型。一旦创建,我们的代码将只需很少的修改即可解决任何数独问题。
配方
确定决策变量
为了将这个问题表述为一个线性规划问题,我们可以简单地为81个方格中的每一个创建一个变量,这些变量代表该方格中的值,范围从1到9。然而,这非常复杂,因为在线性规划中没有“不等于”操作符,因此我们无法使用必要的约束条件,即一个盒子/行/列中的方格值不能相等。虽然我们可以确保一个盒子/行/列中所有值的总和等于45,但这仍然会导致许多满足45约束的解决方案,但同一盒子/行/列中仍然有两个相同的数字。有一种使用大M约束的解决方案,它比较盒子/列/行中每一对值,确定哪个数字严格小于另一个,但我们更倾向于提出一种更加优雅的方法:
我们创建了729个独立的二进制(0-1)问题变量。这些变量代表每个方格的9个问题变量,总共有81个方格,其中每个方格的9个变量分别对应可能在该方格中的数字。变量的二进制性质表示该数字在该方格中的存在是真还是假。因此,每个方格显然只能有9个变量中的1个为真(1),而其他8个必须为假(0),因为任何方格中只能放置一个数字。这一点将在下面变得清晰。
制定目标函数
有趣的是,数独没有比另一个解决方案更好的解决方案,因为根据定义,解决方案必须满足所有约束条件。因此,我们并不是真的在尝试最小化或最大化任何东西,我们只是试图找到满足约束条件的变量值。因此,我们既不设置 LpMinimize 也不设置 LpMaximize,也不定义目标函数。
制定约束条件
这些仅仅是数独问题的已知约束,加上我们自己创建的变量所使用的约束,这些变量用于表达问题的特征:
任何一行中,方格内的数值必须是1到9中的每一个。
任何列中正方形内的值必须是1到9中的每一个。
任何一个方框中的数值必须是1到9中的每一个。(一个方框是整个9x9网格中9个不重叠的3x3网格之一)
在任何方格内必须只有一个数字(这似乎在逻辑上显而易见,但由于我们的变量选择,确保这一点对我们的公式化很重要)。
起始的数独数字在最终解中必须保持原位(这是一个约束,因为这些数字在实际问题中是不可更改的,而我们能控制其他任何数字。如果没有或只有极少数的起始数字,数独问题将会有非常多的可行解,而不仅仅是一个)。
解决方案
介绍性注释和导入语句已输入
"""
The Sudoku Problem Formulation for the PuLP Modeller
Authors: Antony Phillips, Dr Stuart Mitchell
edited by Nathan Sudermann-Merx
"""
# Import PuLP modeler functions
from pulp import *
在数独问题的独特情况下,行名、列名和变量选项值都是从1到9的完全相同的数字列表。
# All rows, columns and values within a Sudoku take values from 1 to 9
VALS = ROWS = COLS = range(1, 10)
创建了一个名为 Boxes 的列表,其中包含9个元素,每个元素又是一个列表。这9个列表分别对应于9个方框,每个列表包含元组作为元素,这些元组包含该方框中每个方格的行和列索引。以类似于以下方式显式输入值会产生相同的效果(但会浪费时间):
# The boxes list is created, with the row and column index of each square in each box
Boxes = [
[(3 * i + k + 1, 3 * j + l + 1) for k in range(3) for l in range(3)]
for i in range(3)
for j in range(3)
]
因此,Boxes[0] 将返回一个包含第一个盒子中每个9个方格位置的元组列表。
prob 变量被创建来包含问题数据。
# The prob variable is created to contain the problem data
prob = LpProblem("Sudoku Problem")
由于 (Vals,Rows,Cols) 为每个值、行和列的组合创建了一个变量,因此创建了729个问题变量。一个示例变量是:Choice_4_2_9,它被定义为一个二进制变量(只能取整数1或0)。如果Choice_4_2_9为1,则意味着数字4位于第2行、第9列的方格中。(如果为0,则意味着该位置没有4)
# The decision variables are created
choices = LpVariable.dicts("Choice", (VALS, ROWS, COLS), cat="Binary")
如上所述,我们不定义目标函数,因为我们只关心任何能满足约束条件的变量组合。
# We do not define an objective function since none is needed
由于每个方格有9个变量,因此指定其中只有一个变量可以取值为1(其余为0)非常重要。因此,以下代码表示:对于81个方格中的每一个,与该特定方格相关的所有9个变量(每个变量代表可能存在的值)的总和必须等于1。
# A constraint ensuring that only one value can be in each square is created
for r in ROWS:
for c in COLS:
prob += lpSum([choices[v][r][c] for v in VALS]) == 1
这些约束确保每个数字(值)在每一行、每一列和每一个方格中只能出现一次。
# The row, column and box constraints are added for each value
for v in VALS:
for r in ROWS:
prob += lpSum([choices[v][r][c] for c in COLS]) == 1
for c in COLS:
prob += lpSum([choices[v][r][c] for r in ROWS]) == 1
for b in Boxes:
prob += lpSum([choices[v][r][c] for (r, c) in b]) == 1
起始数字作为约束条件输入,即第1行第1列的5是正确的。
# The starting numbers are entered as constraints
input_data = [
(5, 1, 1),
(6, 2, 1),
(8, 4, 1),
(4, 5, 1),
(7, 6, 1),
(3, 1, 2),
(9, 3, 2),
(6, 7, 2),
(8, 3, 3),
(1, 2, 4),
(8, 5, 4),
(4, 8, 4),
(7, 1, 5),
(9, 2, 5),
(6, 4, 5),
(2, 6, 5),
(1, 8, 5),
(8, 9, 5),
(5, 2, 6),
(3, 5, 6),
(9, 8, 6),
(2, 7, 7),
(6, 3, 8),
(8, 7, 8),
(7, 9, 8),
(3, 4, 9),
(1, 5, 9),
(6, 6, 9),
(5, 8, 9),
]
for v, r, c in input_data:
prob += choices[v][r][c] == 1
问题被写入一个LP文件,使用PuLP选择的求解器求解,并将解的状态打印到屏幕上
# The problem data is written to an .lp file
prob.writeLP("Sudoku.lp")
# The problem is solved using PuLP's choice of Solver
prob.solve()
# The status of the solution is printed to the screen
print("Status:", LpStatus[prob.status])
与其打印出所有729个二进制问题变量及其各自的值,不如将解决方案绘制在文本文件中更有意义。代码还在每第三行和第三列之间插入线条,以使解决方案更易于阅读。sudokuout.txt文件与.py文件创建在同一文件夹中。
# A file called sudokuout.txt is created/overwritten for writing to
sudokuout = open("sudokuout.txt", "w")
# The solution is written to the sudokuout.txt file
for r in ROWS:
if r in [1, 4, 7]:
sudokuout.write("+-------+-------+-------+\n")
for c in COLS:
for v in VALS:
if value(choices[v][r][c]) == 1:
if c in [1, 4, 7]:
sudokuout.write("| ")
sudokuout.write(str(v) + " ")
if c == 9:
sudokuout.write("|\n")
sudokuout.write("+-------+-------+-------+")
sudokuout.close()
解决方案的位置会被打印到解决方案中。
# The location of the solution is give to the user
print("Solution Written to sudokuout.txt")
完整的文件在上文提供 Sudoku1.py 最终的解决方案应如下所示:
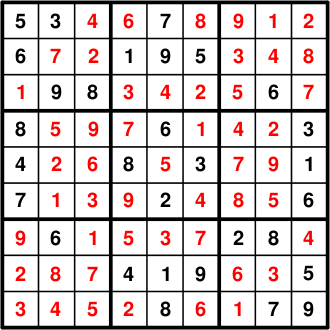
专家额外内容
在上述公式中,我们没有考虑到如果数独问题定义不明确,可能存在多个解的情况。
我们可以通过编辑代码来使我们的代码返回所有解决方案,如在 prob.writeLP 行之后所示。本质上,我们只是在循环执行求解语句,并且在每次成功求解后,添加一个约束条件,即相同的解决方案不能再次使用。当没有更多解决方案时,我们的程序结束。
while True:
prob.solve()
# The status of the solution is printed to the screen
print("Status:", LpStatus[prob.status])
# The solution is printed if it was deemed "optimal" i.e met the constraints
if LpStatus[prob.status] == "Optimal":
# The solution is written to the sudokuout.txt file
for r in ROWS:
if r in [1, 4, 7]:
sudokuout.write("+-------+-------+-------+\n")
for c in COLS:
for v in VALS:
if value(choices[v][r][c]) == 1:
if c in [1, 4, 7]:
sudokuout.write("| ")
sudokuout.write(str(v) + " ")
if c == 9:
sudokuout.write("|\n")
sudokuout.write("+-------+-------+-------+\n\n")
# The constraint is added that the same solution cannot be returned again
prob += (
lpSum(
[
choices[v][r][c]
for v in VALS
for r in ROWS
for c in COLS
if value(choices[v][r][c]) == 1
]
)
<= 80
)
# If a new optimal solution cannot be found, we end the program
else:
break
sudokuout.close()
使用此功能的完整文件可在此处下载:Sudoku2.py。当使用此代码解决具有大量解的数独问题时,可能需要非常长的时间来解决所有问题。要从唯一解的数独问题创建具有多个解的数独问题,您可以简单地删除一个起始数字约束。您可能会发现,删除多个约束仍会导致单一最优解,但删除某个特定约束会导致解的数量突然大幅增加。