scipy.signal.windows.

dpss

scipy.signal.windows.dpss(M, NW, Kmax=None, sym=True, norm=None, return_ratios=False)

计算离散长球面序列 (DPSS)。

DPSS（或Slepian序列）常用于多锥度功率谱密度估计（参见[Re991e28c1f6b-1]_）。序列中的第一个窗口可用于最大化主瓣中的能量集中，也称为Slepian窗口。

参数:

M整数

窗口长度。

NW浮动

标准化的半带宽对应于 2*NW = BW/f0 = BW*M*dt 其中 dt 取为 1。

Kmaxint | None, 可选

要返回的 DPSS 窗口的数量（顺序为 0 到 Kmax-1）。如果为 None（默认），则只返回一个形状为 (M,) 的窗口，而不是形状为 (Kmax, M) 的窗口数组。

symbool, 可选

当为 True 时（默认），生成一个对称的窗口，用于滤波器设计。当为 False 时，生成一个周期性窗口，用于频谱分析。

规范{2, ‘approximate’, ‘subsample’} | 无, 可选

如果为 ‘approximate’ 或 ‘subsample’，则窗口通过最大值进行归一化，并应用一个修正比例因子，用于偶数长度的窗口，使用 M**2/(M**2+NW)``（'approximate'）或基于FFT的子样本移位（'subsample'），详见注释。如果为 None，则在 ``Kmax=None 时使用 ‘approximate’，否则使用 2（使用 l2 范数）。

return_ratiosbool, 可选

如果为 True，除了窗口外，还返回浓度比。

返回:

vndarray, 形状 (Kmax, M) 或 (M,)

DPSS 窗口。如果 Kmax 为 None，则为 1D。

rndarray, 形状 (Kmax,) 或浮点数, 可选

窗口的集中度比率。仅当 return_ratios 评估为 True 时返回。如果 Kmax 为 None，则将为 0D。

注释

此计算使用了 [2] 中给出的三对角特征向量公式。

对于 Kmax=None 的默认归一化，即窗口生成模式，简单地使用 l-infinity 范数会创建一个包含两个单位值的窗口，这会在偶数和奇数阶之间产生轻微的归一化差异。使用偶数样本数的近似修正 M**2/float(M**2+NW) 来抵消这种效果（见下文示例）。

对于非常长的信号（例如，1e6个元素），计算比原信号短几个数量级的窗口可能会有用，并使用插值（例如，scipy.interpolate.interp1d）来获得长度为 M 的窗口，但通常这不会保持窗口之间的正交性。

Added in version 1.1.

参考文献

[1]

Percival DB, Walden WT. 物理应用的谱分析：多锥度和常规单变量技术。剑桥大学出版社；1993年。

[2]

Slepian, D. 扁球面波函数, 傅里叶分析, 和不确定性 V: 离散情况. 贝尔系统技术期刊, 第57卷 (1978), 1371430.

[3]

Kaiser, JF, Schafer RW. 关于在频谱分析中使用 I0-Sinh 窗口的研究。IEEE 声学、语音和信号处理汇刊。ASSP-28 (1): 105-107; 1980.

示例

Try it in your browser!

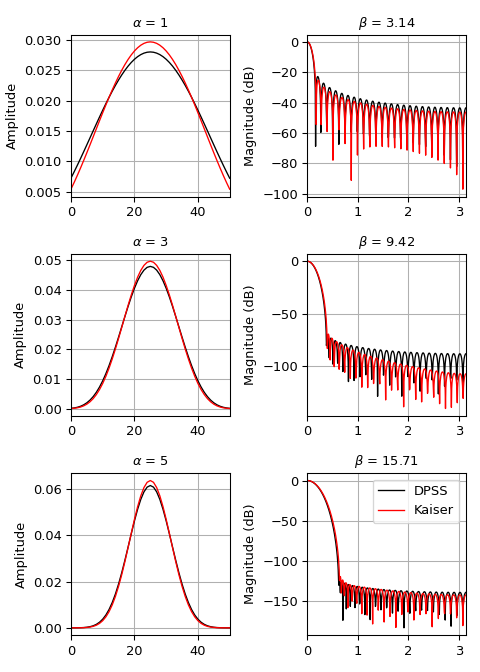
我们可以将窗口与 kaiser 进行比较，后者是为了更容易计算而发明的替代方案 [Re991e28c1f6b-3]_（示例改编自 这里）：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import windows, freqz
>>> M = 51
>>> fig, axes = plt.subplots(3, 2, figsize=(5, 7))
>>> for ai, alpha in enumerate((1, 3, 5)):
...     win_dpss = windows.dpss(M, alpha)
...     beta = alpha*np.pi
...     win_kaiser = windows.kaiser(M, beta)
...     for win, c in ((win_dpss, 'k'), (win_kaiser, 'r')):
...         win /= win.sum()
...         axes[ai, 0].plot(win, color=c, lw=1.)
...         axes[ai, 0].set(xlim=[0, M-1], title=r'$\alpha$ = %s' % alpha,
...                         ylabel='Amplitude')
...         w, h = freqz(win)
...         axes[ai, 1].plot(w, 20 * np.log10(np.abs(h)), color=c, lw=1.)
...         axes[ai, 1].set(xlim=[0, np.pi],
...                         title=r'$\beta$ = %0.2f' % beta,
...                         ylabel='Magnitude (dB)')
>>> for ax in axes.ravel():
...     ax.grid(True)
>>> axes[2, 1].legend(['DPSS', 'Kaiser'])
>>> fig.tight_layout()
>>> plt.show()

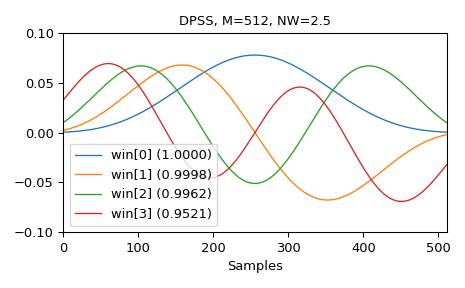
以下是前四个窗口的示例，以及它们的集中度比率：

>>> M = 512
>>> NW = 2.5
>>> win, eigvals = windows.dpss(M, NW, 4, return_ratios=True)
>>> fig, ax = plt.subplots(1)
>>> ax.plot(win.T, linewidth=1.)
>>> ax.set(xlim=[0, M-1], ylim=[-0.1, 0.1], xlabel='Samples',
...        title='DPSS, M=%d, NW=%0.1f' % (M, NW))
>>> ax.legend(['win[%d] (%0.4f)' % (ii, ratio)
...            for ii, ratio in enumerate(eigvals)])
>>> fig.tight_layout()
>>> plt.show()

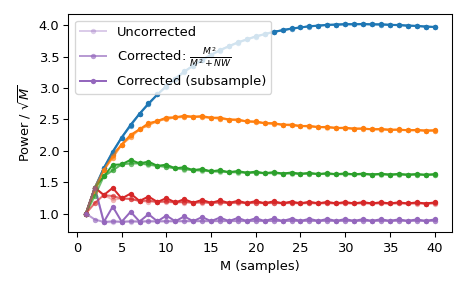
使用标准的 \(l_{\infty}\) 范数会在偶数 M 时产生两个单位值，但在奇数 M 时只产生一个单位值。这会导致不均匀的窗口功率，可以通过近似修正 M**2/float(M**2+NW) 来抵消，可以通过使用 norm='approximate' 来选择（当 Kmax=None 时，这与 norm=None 相同，正如这里的情况）。或者，可以使用较慢的 norm='subsample'，它使用频域（FFT）中的子样本移位来计算修正：

>>> Ms = np.arange(1, 41)
>>> factors = (50, 20, 10, 5, 2.0001)
>>> energy = np.empty((3, len(Ms), len(factors)))
>>> for mi, M in enumerate(Ms):
...     for fi, factor in enumerate(factors):
...         NW = M / float(factor)
...         # Corrected using empirical approximation (default)
...         win = windows.dpss(M, NW)
...         energy[0, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
...         # Corrected using subsample shifting
...         win = windows.dpss(M, NW, norm='subsample')
...         energy[1, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
...         # Uncorrected (using l-infinity norm)
...         win /= win.max()
...         energy[2, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
>>> fig, ax = plt.subplots(1)
>>> hs = ax.plot(Ms, energy[2], '-o', markersize=4,
...              markeredgecolor='none')
>>> leg = [hs[-1]]
>>> for hi, hh in enumerate(hs):
...     h1 = ax.plot(Ms, energy[0, :, hi], '-o', markersize=4,
...                  color=hh.get_color(), markeredgecolor='none',
...                  alpha=0.66)
...     h2 = ax.plot(Ms, energy[1, :, hi], '-o', markersize=4,
...                  color=hh.get_color(), markeredgecolor='none',
...                  alpha=0.33)
...     if hi == len(hs) - 1:
...         leg.insert(0, h1[0])
...         leg.insert(0, h2[0])
>>> ax.set(xlabel='M (samples)', ylabel=r'Power / $\sqrt{M}$')
>>> ax.legend(leg, ['Uncorrected', r'Corrected: $\frac{M^2}{M^2+NW}$',
...                 'Corrected (subsample)'])
>>> fig.tight_layout()

Go BackOpen In Tab