从地理点构建Delaunay图

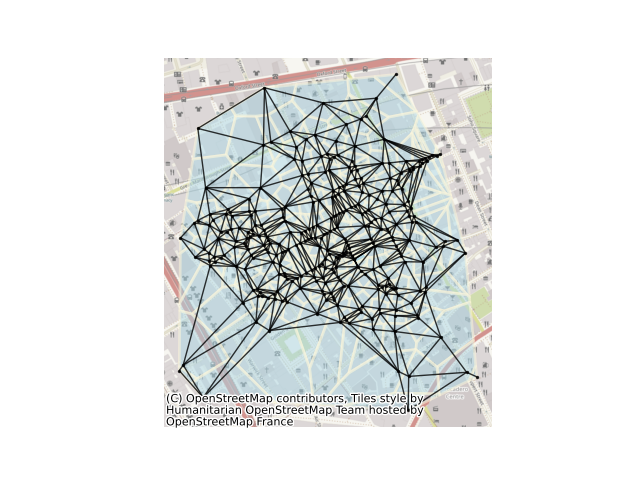
这个示例展示了如何从一组点构建Delaunay图（及其对偶图，即Voronoi多边形集合）。 为此，我们将使用1853年约翰·斯诺记录的宽街水泵附近的霍乱病例数据集。 这里展示的方法也可以直接应用于多边形数据，使用它们的质心作为代表点。

from libpysal import weights, examples
from libpysal.cg import voronoi_frames
from contextily import add_basemap
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import geopandas

# 从GeoPackage文件中读取示例数据。GeoPackage
# 是一种用于存储地理数据的后备格式
# 通过sqlite。geopandas读取数据依赖于fiona包，
# 提供一个高层次的pandas风格接口来处理地理数据。
# GeoPandas 可以读取许多不同类型的地理数据格式。
cases = geopandas.read_file("cholera_cases.gpkg")

# 为了使networkx能够正确绘制我们图形的节点，我们
# 需要构建数据集中每个点的坐标数组。
# 要将这个转换为numpy数组，我们从轨迹中提取x和y坐标
# geometry column.
coordinates = np.column_stack((cases.geometry.x, cases.geometry.y))

# 虽然我们可以直接展示Delaunay图，但对其进行一些处理是有益的
# 将Delaunay图与Voronoi图一起可视化。这是因为
# 两者本质上是相互关联的：Voronoi图的邻接图
# 是生成点集合的Delaunay图！简而言之，这意味着
# 我们可以构建Voronoi图（依赖于scipy.spatial作为底层实现）
# 计算），然后将这些多边形快速转换为Delaunay图。
# 不过要小心；我们的算法默认会将沃罗诺伊图裁剪至
# 点模式的边界框。这由“clip”参数控制。
cells, generators = voronoi_frames(coordinates, clip="convex hull")

# 利用Voronoi多边形，我们可以构建它们之间的邻接图
# "车"邻接性。这表示将沃罗诺伊单元视为相邻，如果它们共享
# 一个边缘/面。这类似于“冯·诺依曼”邻域，或四个基本方向
# 在规则网格中的邻居。这个名字来源于车棋子可以移动的方向
# on a chessboard.
delaunay = weights.Rook.from_dataframe(cells)

# 一旦图构建完成，我们可以使用这些图将其转换为networkx对象
# relevant method.
delaunay_graph = delaunay.to_networkx()

# 要使用networkx进行绘图，我们需要将节点重新合并
# 为了在networkx中绘制，调整它们的位置
positions = dict(zip(delaunay_graph.nodes, coordinates))

# 现在，我们可以使用一个漂亮的底图进行绘制。
ax = cells.plot(facecolor="lightblue", alpha=0.50, edgecolor="cornsilk", linewidth=2)
try:  # 尝试-捕获以处理CI中的超时/解析失败问题
    add_basemap(ax)
except:
    pass

ax.axis("off")
nx.draw(
    delaunay_graph,
    positions,
    ax=ax,
    node_size=2,
    node_color="k",
    edge_color="k",
    alpha=0.8,
)
plt.show()