10. 图像的几何变换

10.1. 裁剪、调整大小和重新缩放图像

图像作为NumPy数组（如 关于图像的NumPy速成课程 部分所述），可以通过简单的切片操作进行裁剪。下面我们裁剪一个对应于宇航员图像左上角的100x100正方形。请注意，此操作是对所有颜色通道进行的（颜色维度是最后一个，即第三个维度）:

>>> import skimage as ski
>>> img = ski.data.astronaut()
>>> top_left = img[:100, :100]

为了改变图像的形状，skimage.color 提供了几种功能，这些功能在 缩放、调整大小和缩小 中有描述。

from skimage import data, color
from skimage.transform import rescale, resize, downscale_local_mean

image = color.rgb2gray(data.astronaut())

image_rescaled = rescale(image, 0.25, anti_aliasing=False)
image_resized = resize(
    image, (image.shape[0] // 4, image.shape[1] // 4), anti_aliasing=True
)
image_downscaled = downscale_local_mean(image, (4, 3))

10.2. 投影变换（单应性）

单应性 是欧几里得空间中保持点对齐的变换。单应性的特定情况对应于更多属性的保持，例如平行性（仿射变换）、形状（相似变换）或距离（欧几里得变换）。scikit-image 中可用的不同类型的单应性在 单应性类型 中展示。

投影变换可以使用显式参数（例如缩放、剪切、旋转和平移）来创建:

import numpy as np
import skimage as ski

tform = ski.transform.EuclideanTransform(
   rotation=np.pi / 12.,
   translation = (100, -20)
   )

或完整的变换矩阵:

matrix = np.array([[np.cos(np.pi/12), -np.sin(np.pi/12), 100],
                   [np.sin(np.pi/12), np.cos(np.pi/12), -20],
                   [0, 0, 1]])
tform = ski.transform.EuclideanTransform(matrix)

变换的变换矩阵可以通过其 tform.params 属性获得。变换可以通过使用 @ 矩阵乘法运算符将矩阵相乘来组合。

变换矩阵使用 齐次坐标，这是欧几里得几何中使用的笛卡尔坐标的扩展，用于更一般的射影几何。特别是，无穷远点可以用有限坐标表示。

可以使用 skimage.transform.warp() 对图像应用变换:

img = ski.util.img_as_float(ski.data.chelsea())
tf_img = ski.transform.warp(img, tform.inverse)

在 skimage.transform 中的不同变换有一个 estimate 方法，用于根据两组点（源点和目标点）估计变换的参数，如 使用几何变换 教程中所解释的:

text = ski.data.text()

src = np.array([[0, 0], [0, 50], [300, 50], [300, 0]])
dst = np.array([[155, 15], [65, 40], [260, 130], [360, 95]])

tform3 = ski.transform.ProjectiveTransform()
tform3.estimate(src, dst)
warped = ski.transform.warp(text, tform3, output_shape=(50, 300))

estimate 方法使用最小二乘优化来最小化源和优化之间的距离。源点和目标点可以手动确定，或者使用 skimage.feature 中可用的不同特征检测方法来确定，例如

• 角点检测,

• ORB 特征检测器和二进制描述符,

• BRIEF 二进制描述符,

• 等等。

并在估计变换参数之前使用 skimage.feature.match_descriptors() 匹配点。然而，常常会产生虚假匹配，建议使用 RANSAC 算法（而不是简单的最小二乘优化）来提高对异常值的鲁棒性，如 使用 RANSAC 进行鲁棒匹配 中所解释的那样。

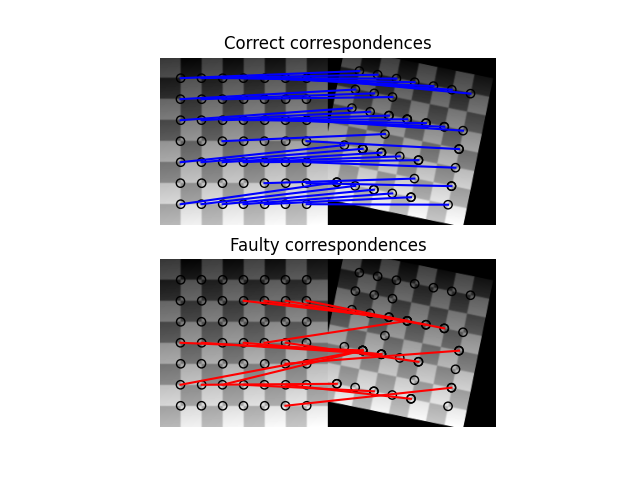
展示变换估计应用的示例是

• 立体匹配 基本矩阵估计 和

• 图像校正 使用几何变换

estimate 方法是基于点的，也就是说，它只使用源图像和目标图像中的一组点。为了估计平移（位移），也可以使用基于傅里叶空间互相关技术的 全场 方法，该方法使用所有像素。这种方法由 skimage.registration.phase_cross_correlation() 实现，并在 图像配准 教程中进行了解释。

教程 使用极坐标和极对数变换进行配准 解释了通过首先使用对数极坐标变换来估计旋转的全场方法的变体。