使用 sktime 进行预测 - 附录：预测、监督回归以及混淆两者的陷阱

本笔记本提供了一些关于在 sktime 中实现的预测与 scikit-learn 和类似工具箱支持的非常常见的监督预测任务之间关系的补充说明。

本笔记本中讨论的要点：

• 预测与监督预测不同；

• 尽管预测可以通过监督预测算法“解决”，但这是一种间接的方法，需要仔细的组合；

• 从接口的角度来看，这被正确地表述为“简化”，即，在预测器中使用监督预测器作为组件；

• 如果手动完成，可能会遇到一些陷阱——例如，过于乐观的性能评估、信息泄露，或“预测过去”类型的错误。

# general imports
import numpy as np
import pandas as pd

误诊预测为监督回归的陷阱

一个常见的错误是将预测问题误认为是监督回归问题——毕竟，在这两种情况下我们都是预测数字，所以这肯定是同一件事吗？

确实，我们在两者中都预测数字，但设置是不同的：

• 在监督回归中，我们根据 特征变量 预测 标签/目标变量 ，在横截面设置中进行。这是在基于标签/特征示例进行训练之后。

• 在预测中，我们根据 同一变量 的 过去值 来预测 未来值 ，这在时间/顺序设置中进行。这是在基于过去进行训练之后。

在常见的数据框表示中：

• 在监督回归中，我们根据其他列预测某一列的条目。为此，我们主要利用这些列之间的统计关系，这些关系是从完整的行示例中学习到的。所有行都被假定为可交换的。

• 在预测中，我们预测新行，假设行之间有时间顺序。为此，我们主要利用从前行和后续行之间的统计关系，这些关系是从观察到的行序列的例子中学到的。这些行不是可交换的，而是按时间顺序排列的。

陷阱1：性能评估中的过度乐观，对“损坏”预测器的错误信心

混淆这两个任务可能导致信息泄露和过于乐观的性能评估。这是因为，在监督回归中，行的顺序并不重要，训练/测试分割通常是均匀进行的。在预测中，顺序在训练和评估中都很重要。

虽然看似微妙，但这可能会有重大的实际后果——因为它可能导致人们错误地认为一个“损坏”的方法是高效的，这可能会在实际部署中对健康、财产和其他资产造成损害。

下面的示例展示了“有问题”的性能估计，当错误地使用回归评估工作流程进行预测时。

from sklearn.model_selection import train_test_split

from sktime.datasets import load_airline
from sktime.split import temporal_train_test_split
from sktime.utils.plotting import plot_series

y = load_airline()

y_train, y_test = train_test_split(y)
plot_series(y_train.sort_index(), y_test.sort_index(), labels=["y_train", "y_test"]);

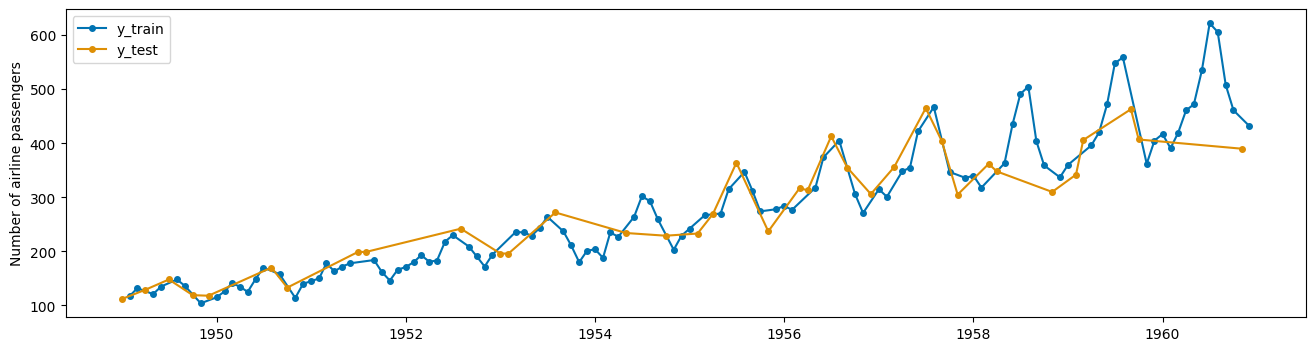
这会导致泄漏：

您用于训练机器学习算法的数据恰好包含您试图预测的信息。

但是 train_test_split(y, shuffle=False) 可以工作，这正是 sktime 中的 temporal_train_test_split(y) 所做的：

y_train, y_test = temporal_train_test_split(y)
plot_series(y_train, y_test, labels=["y_train", "y_test"]);

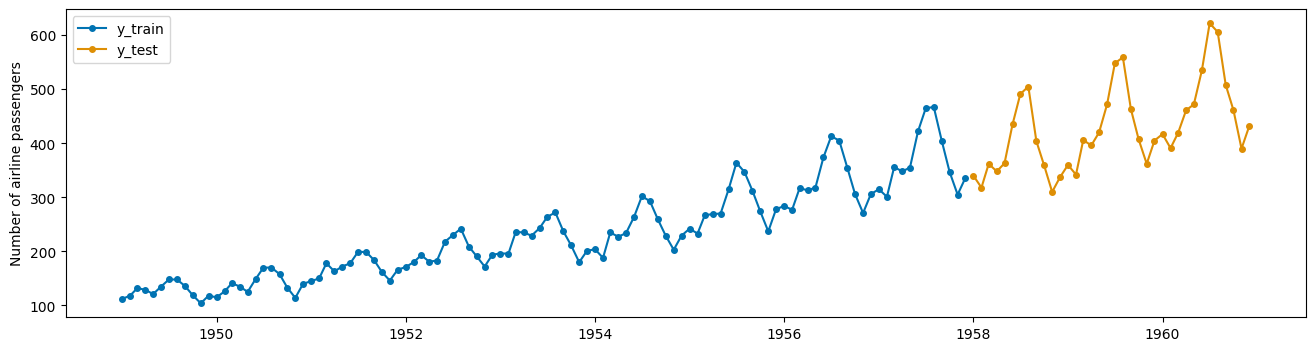
陷阱2：晦涩的数据操作，应用回归器的脆弱样板代码

在通过滞后（例如，在自回归减少策略中）转换数据以进行预测后，应用监督回归器是一种常见做法。

在开始时会出现两个重要的陷阱：

• 为了将数据转换为适合拟合的形式，必须编写大量的样板代码 - 这很容易出错

• 这里有一些隐含的超参数，例如窗口和滞后大小。如果不谨慎处理，这些参数在实验中既不明确也不被跟踪，这可能导致“p值操纵”。

以下是一个此类样板代码的示例，以演示这一点。该代码紧密模仿了用于 M4 竞赛 中的 R 代码：

# suppose we want to predict 3 years ahead
fh = np.arange(1, 37)

# slightly modified code from the M4 competition


def split_into_train_test(data, in_num, fh):
    """Split the series into train and test sets.

    Each step takes multiple points as inputs
    :param data: an individual TS
    :param fh: number of out of sample points
    :param in_num: number of input points for the forecast
    :return:
    """
    train, test = data[:-fh], data[-(fh + in_num) :]
    x_train, y_train = train[:-1], np.roll(train, -in_num)[:-in_num]
    x_test, y_test = test[:-1], np.roll(test, -in_num)[:-in_num]
    #     x_test, y_test = train[-in_num:], np.roll(test, -in_num)[:-in_num]

    # reshape input to be [samples, time steps, features]
    # (N-NF samples, 1 time step, 1 feature)
    x_train = np.reshape(x_train, (-1, 1))
    x_test = np.reshape(x_test, (-1, 1))
    temp_test = np.roll(x_test, -1)
    temp_train = np.roll(x_train, -1)
    for _ in range(1, in_num):
        x_train = np.concatenate((x_train[:-1], temp_train[:-1]), 1)
        x_test = np.concatenate((x_test[:-1], temp_test[:-1]), 1)
        temp_test = np.roll(temp_test, -1)[:-1]
        temp_train = np.roll(temp_train, -1)[:-1]

    return x_train, y_train, x_test, y_test

# here we split the time index, rather than the actual values,
# to show how we split the windows
feature_window, target_window, _, _ = split_into_train_test(
    np.arange(len(y)), 10, len(fh)
)

为了更好地理解先前的数据转换，我们可以看看如何将训练序列分割成窗口。这里我们展示了生成的窗口，表示为整数索引：

feature_window[:5, :]

array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9],
       [ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10],
       [ 2,  3,  4,  5,  6,  7,  8,  9, 10, 11],
       [ 3,  4,  5,  6,  7,  8,  9, 10, 11, 12],
       [ 4,  5,  6,  7,  8,  9, 10, 11, 12, 13]])

target_window[:5]

array([10, 11, 12, 13, 14])

# now we can split the actual values of the time series
x_train, y_train, x_test, y_test = split_into_train_test(y.values, 10, len(fh))
print(x_train.shape, y_train.shape)

(98, 10) (98,)

from sklearn.ensemble import RandomForestRegressor

model = RandomForestRegressor()
model.fit(x_train, y_train)

RandomForestRegressor()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

再次强调这里的潜在陷阱：

手册需要大量的手写代码，这些代码通常容易出错，不具备模块化特性，且难以调整。

这些步骤涉及许多隐含的超参数：

• 你将时间序列分割成窗口的方式（例如，窗口长度）；

• 你生成预测的方式（递归策略、直接策略、其他混合策略）。

陷阱3：给定一个拟合的回归算法，我们如何生成预测？

下一个重要的陷阱出现在结尾：

如果在监督回归器的“手动路径”上进行预测，监督回归器的输出必须转换回预测值。这很容易被遗忘，并且会导致预测和评估中的错误（参见陷阱1）——特别是，如果不清楚地跟踪哪些数据在什么时间已知，或者如何反转拟合中进行的转换。

一个天真的用户现在可能会这样进行：

print(x_test.shape, y_test.shape)

# add back time index to y_test
y_test = pd.Series(y_test, index=y.index[-len(fh) :])

(36, 10) (36,)

y_pred = model.predict(x_test)

from sktime.performance_metrics.forecasting import mean_absolute_percentage_error

mean_absolute_percentage_error(
    y_test, pd.Series(y_pred, index=y_test.index), symmetric=False
)

0.10892546588134275

如此简单，如此错误……但问题出在哪里呢？这有点微妙，不容易发现：

我们实际上并没有进行最多到第36步的多步预测。相反，我们总是使用最新的数据进行36次单步预测。但这解决的是一个不同的学习任务！

为了解决这个问题，我们可以编写一些代码来递归地执行，就像在M4竞赛中那样：

# slightly modified code from the M4 study
predictions = []
last_window = x_train[-1, :].reshape(1, -1)  # make it into 2d array

last_prediction = model.predict(last_window)[0]  # take value from array

for i in range(len(fh)):
    # append prediction
    predictions.append(last_prediction)

    # update last window using previously predicted value
    last_window[0] = np.roll(last_window[0], -1)
    last_window[0, (len(last_window[0]) - 1)] = last_prediction

    # predict next step ahead
    last_prediction = model.predict(last_window)[0]

y_pred_rec = pd.Series(predictions, index=y_test.index)

from sktime.performance_metrics.forecasting import mean_absolute_percentage_error

mean_absolute_percentage_error(
    y_test, pd.Series(y_pred_rec, index=y_test.index), symmetric=False
)

0.19738808156953527

总结这里的潜在陷阱：

获取回归器预测并将其转换回预测结果并非易事且容易出错：* 需要编写一些样板代码，这与陷阱2类似，引入了潜在的问题；* 一开始并不明显需要编写这些样板代码，从而产生了一个微妙的失败点。

sktime 如何帮助避免上述陷阱？

sktime 通过以下方式缓解了上述陷阱：

• 其统一的预测器接口 - 任何生成预测的策略都是一个预测器。通过统一的接口，预测器可以直接兼容适用于预测器的部署和评估工作流程；

• 它的声明式规范接口减少了样板代码——它被简化到仅包含告诉 sktime 你想构建哪个预测器所需的必要信息。

尽管如此，sktime 旨在保持灵活性，并尽量避免将用户限制在特定的方法选择上。

from sklearn.neighbors import KNeighborsRegressor

from sktime.forecasting.compose import make_reduction

# declarative forecaster specification - just two lines!
regressor = KNeighborsRegressor(n_neighbors=1)
forecaster = make_reduction(regressor, window_length=15, strategy="recursive")

forecaster.fit(y_train)
y_pred = forecaster.predict(fh)

… 就是这样！

请注意，这里没有 x_train 或其他样板文件，因为滞后特征的构建和其他样板代码由预测器内部处理。

有关 sktime 组合接口的更多详细信息，请参阅主要预测教程的第3节。

---

使用 nbsphinx 生成。Jupyter 笔记本可以在 这里 找到。