使用 sktime 进行概率预测#
最初在 pydata Berlin 2022 上展示,视频演示请参见
本笔记本概述#
快速开始 - 概率预测
消除歧义 - 概率预测的类型
详细信息:概率预测接口
概率预测的指标和评估
高级组合:管道、调优、简化
扩展指南
贡献者荣誉
[1]:
import warnings
warnings.filterwarnings("ignore")
快速入门 - 使用 sktime 进行概率预测#
… 的工作原理与基本的预测工作流程完全相同,只需将 predict 替换为概率方法!
[2]:
from sktime.datasets import load_airline
from sktime.forecasting.arima import ARIMA
# step 1: data specification
y = load_airline()
# step 2: specifying forecasting horizon
fh = [1, 2, 3]
# step 3: specifying the forecasting algorithm
forecaster = ARIMA()
# step 4: fitting the forecaster
forecaster.fit(y, fh=[1, 2, 3])
# step 5: querying predictions
y_pred = forecaster.predict()
# for probabilistic forecasting:
# call a probabilistic forecasting method after or instead of step 5
y_pred_int = forecaster.predict_interval(coverage=0.9)
y_pred_int
[2]:
| Number of airline passengers | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1961-01 | 371.535093 | 481.554608 |
| 1961-02 | 344.853205 | 497.712761 |
| 1961-03 | 324.223995 | 508.191104 |
``sktime`` 中的概率预测方法:
预测区间 -
predict_interval(fh=None, X=None, coverage=0.90)预测分位数 -
predict_quantiles(fh=None, X=None, alpha=[0.05, 0.95])预测方差 -
predict_var(fh=None, X=None, cov=False)分布预测 -
predict_proba(fh=None, X=None, marginal=True)
要检查 sktime 中哪些预测器支持概率预测,请使用 registry.all_estimators 工具并查找具有 capability:pred_int 标签(值为 True)的估计器。
对于如管道这样的复合结构,一个正标签意味着如果(某些或所有)组件支持,逻辑就会实现。
[3]:
from sktime.registry import all_estimators
all_estimators(
"forecaster", filter_tags={"capability:pred_int": True}, as_dataframe=True
)
[3]:
| name | object | |
|---|---|---|
| 0 | ARCH | <class 'sktime.forecasting.arch._uarch.ARCH'> |
| 1 | ARIMA | <class 'sktime.forecasting.arima.ARIMA'> |
| 2 | AutoARIMA | <class 'sktime.forecasting.arima.AutoARIMA'> |
| 3 | AutoETS | <class 'sktime.forecasting.ets.AutoETS'> |
| 4 | BATS | <class 'sktime.forecasting.bats.BATS'> |
| 5 | BaggingForecaster | <class 'sktime.forecasting.compose._bagging.Ba... |
| 6 | ColumnEnsembleForecaster | <class 'sktime.forecasting.compose._column_ens... |
| 7 | ConformalIntervals | <class 'sktime.forecasting.conformal.Conformal... |
| 8 | DynamicFactor | <class 'sktime.forecasting.dynamic_factor.Dyna... |
| 9 | FhPlexForecaster | <class 'sktime.forecasting.compose._fhplex.FhP... |
| 10 | ForecastX | <class 'sktime.forecasting.compose._pipeline.F... |
| 11 | ForecastingGridSearchCV | <class 'sktime.forecasting.model_selection._tu... |
| 12 | ForecastingPipeline | <class 'sktime.forecasting.compose._pipeline.F... |
| 13 | ForecastingRandomizedSearchCV | <class 'sktime.forecasting.model_selection._tu... |
| 14 | ForecastingSkoptSearchCV | <class 'sktime.forecasting.model_selection._tu... |
| 15 | NaiveForecaster | <class 'sktime.forecasting.naive.NaiveForecast... |
| 16 | NaiveVariance | <class 'sktime.forecasting.naive.NaiveVariance'> |
| 17 | Permute | <class 'sktime.forecasting.compose._pipeline.P... |
| 18 | Prophet | <class 'sktime.forecasting.fbprophet.Prophet'> |
| 19 | SARIMAX | <class 'sktime.forecasting.sarimax.SARIMAX'> |
| 20 | SquaringResiduals | <class 'sktime.forecasting.squaring_residuals.... |
| 21 | StatsForecastARCH | <class 'sktime.forecasting.arch._statsforecast... |
| 22 | StatsForecastAutoARIMA | <class 'sktime.forecasting.statsforecast.Stats... |
| 23 | StatsForecastAutoCES | <class 'sktime.forecasting.statsforecast.Stats... |
| 24 | StatsForecastAutoETS | <class 'sktime.forecasting.statsforecast.Stats... |
| 25 | StatsForecastAutoTheta | <class 'sktime.forecasting.statsforecast.Stats... |
| 26 | StatsForecastGARCH | <class 'sktime.forecasting.arch._statsforecast... |
| 27 | StatsForecastMSTL | <class 'sktime.forecasting.statsforecast.Stats... |
| 28 | TBATS | <class 'sktime.forecasting.tbats.TBATS'> |
| 29 | ThetaForecaster | <class 'sktime.forecasting.theta.ThetaForecast... |
| 30 | TransformedTargetForecaster | <class 'sktime.forecasting.compose._pipeline.T... |
| 31 | UnobservedComponents | <class 'sktime.forecasting.structural.Unobserv... |
| 32 | VAR | <class 'sktime.forecasting.var.VAR'> |
| 33 | VECM | <class 'sktime.forecasting.vecm.VECM'> |
| 34 | YfromX | <class 'sktime.forecasting.compose._reduce.Yfr... |
什么是概率预测?#
直觉#
生成预测的低/高情景
量化预测中的不确定性
生成预测的预期变化范围
接口视图#
想要 生成预测值的“分布”或“范围”,
在由 预测范围 fh 定义的时间戳处
给定 过去的数据 y (序列),以及可能的外生数据 X
输入到 fit 或 predict:fh,y,X
输出,来自 predict_probabilistic:一些“分布”或“范围”对象
重要警告:有多种可能的方式来建模“分布”或“范围”!
在实践中使用且容易混淆!(而且经常,实际上,混淆!)
正式视图(内生性,一个预测时间戳)#
设 \(y(t_1), \dots, y(t_n)\) 为在固定时间戳 \(t_1, \dots, t_n\) 处的观测值。
(我们考虑 \(y\) 为一个 \(\mathbb{R}^n\) 值的随机变量)
设 \(y'\) 为一个(真实)值,它将在未来的时间戳 \(\tau\) 被观测到。
(我们考虑 \(y'\) 为一个 \(\mathbb{R}\) 值的随机变量)
我们有以下 \(y'\) 的“预测类型”:
名称 |
参数 |
预测/估计 |
|
|---|---|---|---|
点预测 |
条件期望 \(\mathbb{E}[y'\|y]\) |
|
|
方差预测 |
条件方差 \(Var[y'|y]\) |
|
|
分位数预测 |
\(\alpha\in (0,1)\) |
\(\alpha\)-分位数 of \(y'\|y\) |
|
区间预测 |
\(c\in (0,1)\) |
\([a,b]\) 使得 \(P(a\le y' \le b\| y) = c\) |
|
|
\(y'\|y\) 的法则/分布 |
|
注释:
不同的预测者有不同的能力!
指标、评估与调优因“预测类型”而异
排版器可以“添加”预测类型!示例:bootstrap
更多正式细节与直觉:#
“点预测” 是对条件期望 \(\mathbb{E}[y'|y]\) 的预测/估计。直觉:“在多次重复/世界中,这个值是所有观测值的算术平均值”。
“方差预测” 是对条件期望 \(Var[y'|y]\) 的预测/估计。直觉: “在多次重复/世界中,这个值是观测值到完美点预测的平均平方距离”。
一个**“分位数预测”,在分位点 :math:`alphain (0,1)` 处,是对 :math:`y’|y` 的 :math:`alpha`-分位数的预测/估计,即 :math:`F^{-1}_{y’|y}(alpha)`,其中 :math:`F^{-1}` 是随机变量 y’|y 的(广义)逆累积分布函数 = 分位数函数。**直觉:“在多次重复/世界中,恰好有 \(\alpha\) 的比例将等于或小于此值。”
一个具有(对称)覆盖率 \(c\in (0,1)\) 的 “区间预测” 或 “预测区间” 是指一对下界 \(a\) 和上界 \(b\) 的预测/估计,使得 \(P(a\le y' \le b| y) = c\) 且 \(P(y' \gneq b| y) = P(y' \lneq a| y) = (1 - c) /2\)。直觉:“在多次重复/多个世界中,恰好有 \(c\) 的比例会落在区间 \([a,b]\) 内,且高于区间和低于区间的概率相等”。
“分布预测” 或 “完全概率预测” 是对 \(y'|y\) 分布的预测/估计,例如,“它是一个均值为42,方差为1的正态分布”。直觉:对多次重复/世界的生成机制的详尽描述。
注释:
区间预测的上下限是分位数预测在分位数点 \(0.5 - c/2\) 和 \(0.5 + c/2\) 处的预测(只要预测分布是绝对连续的)。
所有其他预测都可以从完整的概率预测中获得;完整的概率预测可以从所有分位数预测或所有区间预测中获得。
其他类型的预测(点预测或方差预测与分位数预测)之间没有确切的关系。
特别是,点预测不需要是中位数预测,即0.5分位数预测。可以是任意 \(\alpha\) 分位数!
文献与Python包中常见的混淆:* 覆盖率 c 与分位数 \alpha * 覆盖率 c 与显著性 p = 1-c * 下界区间的分位数 p/2 与 p * 区间预测与相关但实质上不同的概念:预测均值的置信区间;预测均值的贝叶斯后验或可信区间 * 所有预测都可以是贝叶斯的,混淆:“后验是不同的”或“必须以不同方式评估”
sktime 中的概率预测接口#
本节:
概率预测方法的演练
在更新/预测工作流中使用
多变量和层次数据
所有带有标签 capability:pred_int 的预测者提供以下内容:
预测区间 -
predict_interval(fh=None, X=None, coverage=0.90)预测分位数 -
predict_quantiles(fh=None, X=None, alpha=[0.05, 0.95])预测方差 -
predict_var(fh=None, X=None, cov=False)分布预测 -
predict_proba(fh=None, X=None, marginal=True)
概述:
方法不改变状态,可以多次调用
fh是可选的,如果传递晚了外生数据
X可以被传递
[4]:
import numpy as np
from sktime.datasets import load_airline
from sktime.forecasting.theta import ThetaForecaster
# until fit, identical with the simple workflow
y = load_airline()
fh = np.arange(1, 13)
forecaster = ThetaForecaster(sp=12)
forecaster.fit(y, fh=fh)
[4]:
ThetaForecaster(sp=12)Please rerun this cell to show the HTML repr or trust the notebook.
ThetaForecaster(sp=12)
fh - 预测范围(如果在 fit 中看到则不必要)coverage, 浮点数或浮点数列表, 默认=0.9pandas.DataFramefhcoverage 中的覆盖率分数条目 = 在名义覆盖率下,第二层级的下限/上限预测,对于第一层级的变量,对于行中的时间
[5]:
coverage = 0.9
y_pred_ints = forecaster.predict_interval(coverage=coverage)
y_pred_ints
[5]:
| Number of airline passengers | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1961-01 | 418.280121 | 464.281951 |
| 1961-02 | 402.215881 | 456.888055 |
| 1961-03 | 459.966113 | 522.110500 |
| 1961-04 | 442.589309 | 511.399214 |
| 1961-05 | 443.525027 | 518.409480 |
| 1961-06 | 506.585814 | 587.087737 |
| 1961-07 | 561.496768 | 647.248956 |
| 1961-08 | 557.363322 | 648.062363 |
| 1961-09 | 477.658055 | 573.047752 |
| 1961-10 | 407.915090 | 507.775355 |
| 1961-11 | 346.942924 | 451.082017 |
| 1961-12 | 394.708221 | 502.957142 |
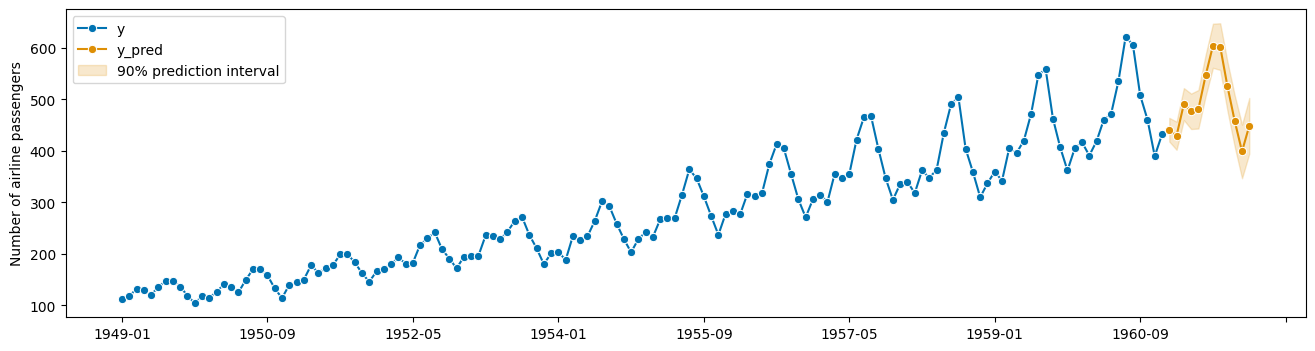
预测区间预测的漂亮绘图:
[6]:
from sktime.utils import plotting
# also requires predictions
y_pred = forecaster.predict()
fig, ax = plotting.plot_series(
y, y_pred, labels=["y", "y_pred"], pred_interval=y_pred_ints
)
ax.legend();
多重覆盖:
[7]:
coverage = [0.5, 0.9, 0.95]
y_pred_ints = forecaster.predict_interval(coverage=coverage)
y_pred_ints
[7]:
| Number of airline passengers | ||||||
|---|---|---|---|---|---|---|
| 0.50 | 0.90 | 0.95 | ||||
| lower | upper | lower | upper | lower | upper | |
| 1961-01 | 431.849266 | 450.712806 | 418.280121 | 464.281951 | 413.873755 | 468.688317 |
| 1961-02 | 418.342514 | 440.761421 | 402.215881 | 456.888055 | 396.979011 | 462.124925 |
| 1961-03 | 478.296822 | 503.779790 | 459.966113 | 522.110500 | 454.013504 | 528.063109 |
| 1961-04 | 462.886144 | 491.102379 | 442.589309 | 511.399214 | 435.998232 | 517.990291 |
| 1961-05 | 465.613670 | 496.320837 | 443.525027 | 518.409480 | 436.352089 | 525.582418 |
| 1961-06 | 530.331440 | 563.342111 | 506.585814 | 587.087737 | 498.874797 | 594.798754 |
| 1961-07 | 586.791063 | 621.954661 | 561.496768 | 647.248956 | 553.282845 | 655.462879 |
| 1961-08 | 584.116789 | 621.308897 | 557.363322 | 648.062363 | 548.675556 | 656.750129 |
| 1961-09 | 505.795123 | 544.910684 | 477.658055 | 573.047752 | 468.520987 | 582.184821 |
| 1961-10 | 437.370840 | 478.319605 | 407.915090 | 507.775355 | 398.349800 | 517.340645 |
| 1961-11 | 377.660798 | 420.364142 | 346.942924 | 451.082017 | 336.967779 | 461.057162 |
| 1961-12 | 426.638370 | 471.026993 | 394.708221 | 502.957142 | 384.339408 | 513.325954 |
fh - 预测范围(如果在 fit 中看到则不必要)alpha,浮点数或浮点数列表,默认值 = [0.1, 0.9]pandas.DataFramefhalpha 中的分位点条目 = 在第2级分位点处的分位数预测,对于第1级中的变量,对于行中的时间
[8]:
alpha = [0.1, 0.25, 0.5, 0.75, 0.9]
y_pred_quantiles = forecaster.predict_quantiles(alpha=alpha)
y_pred_quantiles
[8]:
| Number of airline passengers | |||||
|---|---|---|---|---|---|
| 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | |
| 1961-01 | 423.360378 | 431.849266 | 441.281036 | 450.712806 | 459.201694 |
| 1961-02 | 408.253656 | 418.342514 | 429.551968 | 440.761421 | 450.850279 |
| 1961-03 | 466.829089 | 478.296822 | 491.038306 | 503.779790 | 515.247523 |
| 1961-04 | 450.188398 | 462.886144 | 476.994261 | 491.102379 | 503.800124 |
| 1961-05 | 451.794965 | 465.613670 | 480.967253 | 496.320837 | 510.139542 |
| 1961-06 | 515.476123 | 530.331440 | 546.836776 | 563.342111 | 578.197428 |
| 1961-07 | 570.966895 | 586.791063 | 604.372862 | 621.954661 | 637.778829 |
| 1961-08 | 567.379760 | 584.116789 | 602.712843 | 621.308897 | 638.045925 |
| 1961-09 | 488.192511 | 505.795123 | 525.352904 | 544.910684 | 562.513297 |
| 1961-10 | 418.943257 | 437.370840 | 457.845222 | 478.319605 | 496.747188 |
| 1961-11 | 358.443627 | 377.660798 | 399.012470 | 420.364142 | 439.581313 |
| 1961-12 | 406.662797 | 426.638370 | 448.832681 | 471.026993 | 491.002565 |
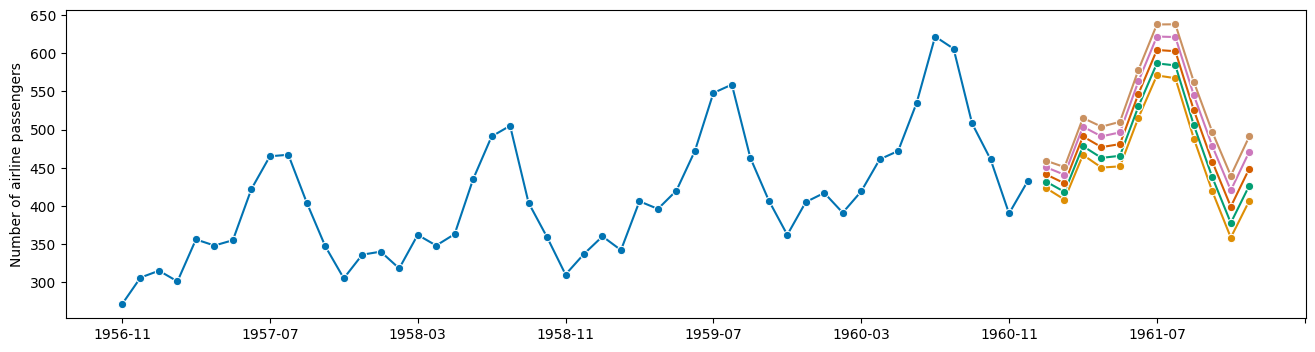
绘制分位数区间预测的漂亮图表:
[9]:
from sktime.utils import plotting
columns = [y_pred_quantiles[i] for i in y_pred_quantiles.columns]
fig, ax = plotting.plot_series(y[-50:], *columns)
fh - 预测范围(如果在 fit 中看到则不必要)cov,布尔值,默认=False条目 = 变量的方差预测,按列排列,按时间排列
[10]:
y_pred_variance = forecaster.predict_var()
y_pred_variance
[10]:
| Number of airline passengers | |
|---|---|
| 1961-01 | 195.540049 |
| 1961-02 | 276.196510 |
| 1961-03 | 356.852970 |
| 1961-04 | 437.509430 |
| 1961-05 | 518.165890 |
| 1961-06 | 598.822350 |
| 1961-07 | 679.478810 |
| 1961-08 | 760.135270 |
| 1961-09 | 840.791730 |
| 1961-10 | 921.448190 |
| 1961-11 | 1002.104650 |
| 1961-12 | 1082.761110 |
使用协方差,使用一个可以返回协方差预测的预测器:
pandas.DataFrame ,其中 fh 用于索引行和列;[11]:
from sktime.forecasting.naive import NaiveVariance
forecaster_with_covariance = NaiveVariance(forecaster)
forecaster_with_covariance.fit(y=y, fh=fh)
forecaster_with_covariance.predict_var(cov=True)
[11]:
| 1961-01 | 1961-02 | 1961-03 | 1961-04 | 1961-05 | 1961-06 | 1961-07 | 1961-08 | 1961-09 | 1961-10 | 1961-11 | 1961-12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1961-01 | 292.337333 | 255.742991 | 264.805437 | 227.703049 | 146.093848 | 154.452828 | 157.976795 | 105.160767 | 78.330263 | 81.835807 | 78.048880 | 197.364510 |
| 1961-02 | 255.742991 | 422.704601 | 402.539255 | 353.437043 | 291.205404 | 236.587874 | 227.199374 | 205.653010 | 152.067425 | 121.629138 | 156.199110 | 245.437907 |
| 1961-03 | 264.805437 | 402.539255 | 588.085328 | 506.095455 | 426.997512 | 394.503923 | 311.457837 | 282.072145 | 243.688600 | 185.938840 | 185.070360 | 305.461211 |
| 1961-04 | 227.703049 | 353.437043 | 506.095455 | 634.350443 | 526.180879 | 482.653094 | 422.777303 | 323.453741 | 280.749312 | 242.065788 | 211.397164 | 294.971031 |
| 1961-05 | 146.093848 | 291.205404 | 426.997512 | 526.180879 | 628.659343 | 570.277520 | 499.460184 | 419.166444 | 325.582777 | 281.608605 | 269.847439 | 318.534675 |
| 1961-06 | 154.452828 | 236.587874 | 394.503923 | 482.653094 | 570.277520 | 728.132497 | 629.184840 | 527.767034 | 444.690518 | 330.643655 | 313.248426 | 382.803216 |
| 1961-07 | 157.976795 | 227.199374 | 311.457837 | 422.777303 | 499.460184 | 629.184840 | 753.550004 | 629.138725 | 536.407567 | 441.998605 | 352.570966 | 415.110916 |
| 1961-08 | 105.160767 | 205.653010 | 282.072145 | 323.453741 | 419.166444 | 527.767034 | 629.138725 | 729.423304 | 615.142491 | 506.155614 | 439.994838 | 430.992291 |
| 1961-09 | 78.330263 | 152.067425 | 243.688600 | 280.749312 | 325.582777 | 444.690518 | 536.407567 | 615.142491 | 744.225561 | 609.227140 | 527.489573 | 546.637585 |
| 1961-10 | 81.835807 | 121.629138 | 185.938840 | 242.065788 | 281.608605 | 330.643655 | 441.998605 | 506.155614 | 609.227140 | 697.805479 | 590.542043 | 604.681130 |
| 1961-11 | 78.048880 | 156.199110 | 185.070360 | 211.397164 | 269.847439 | 313.248426 | 352.570966 | 439.994838 | 527.489573 | 590.542043 | 706.960626 | 698.982580 |
| 1961-12 | 197.364510 | 245.437907 | 305.461211 | 294.971031 | 318.534675 | 382.803216 | 415.110916 | 430.992291 | 546.637585 | 604.681130 | 698.982580 | 913.698229 |
fh - 预测范围(如果在 fit 中看到则不必要)marginal, bool, 可选, 默认=Truemarginal=False)tensorflow-probability Distribution 对象 (需要安装 tensorflow)marginal=False:事件形状为2D,[len(fh), len(y.columns)][12]:
y_pred_dist = forecaster.predict_proba()
y_pred_dist
[12]:
Normal(columns=Index(['Number of airline passengers'], dtype='object'),
index=PeriodIndex(['1961-01', '1961-02', '1961-03', '1961-04', '1961-05', '1961-06',
'1961-07', '1961-08', '1961-09', '1961-10', '1961-11', '1961-12'],
dtype='period[M]'),
mu= Number of airline passengers
1961-01 441.281036
1961-02 429.551968
1961-03 491.038306
1961-04 476.994261
1961-05 480.967253
1961-06 546.836776
1961-07 604.372862
1961-08 602.712843
1961-09 525.352904
1961-10 457.845222
1961-11 399.012470
1961-12 448.832681,
sigma= Number of airline passengers
1961-01 13.983564
1961-02 16.619161
1961-03 18.890552
1961-04 20.916726
1961-05 22.763257
1961-06 24.470847
1961-07 26.066814
1961-08 27.570551
1961-09 28.996409
1961-10 30.355365
1961-11 31.656037
1961-12 32.905336)Please rerun this cell to show the HTML repr or trust the notebook.Normal(columns=Index(['Number of airline passengers'], dtype='object'),
index=PeriodIndex(['1961-01', '1961-02', '1961-03', '1961-04', '1961-05', '1961-06',
'1961-07', '1961-08', '1961-09', '1961-10', '1961-11', '1961-12'],
dtype='period[M]'),
mu= Number of airline passengers
1961-01 441.281036
1961-02 429.551968
1961-03 491.038306
1961-04 476.994261
1961-05 480.967253
1961-06 546.836776
1961-07 604.372862
1961-08 602.712843
1961-09 525.352904
1961-10 457.845222
1961-11 399.012470
1961-12 448.832681,
sigma= Number of airline passengers
1961-01 13.983564
1961-02 16.619161
1961-03 18.890552
1961-04 20.916726
1961-05 22.763257
1961-06 24.470847
1961-07 26.066814
1961-08 27.570551
1961-09 28.996409
1961-10 30.355365
1961-11 31.656037
1961-12 32.905336)[13]:
# obtaining quantiles
y_pred_dist.quantile([0.1, 0.9])
[13]:
| Number of airline passengers | ||
|---|---|---|
| 0.1 | 0.9 | |
| 1961-01 | 423.360378 | 459.201694 |
| 1961-02 | 408.253656 | 450.850279 |
| 1961-03 | 466.829089 | 515.247523 |
| 1961-04 | 450.188398 | 503.800124 |
| 1961-05 | 451.794965 | 510.139542 |
| 1961-06 | 515.476123 | 578.197428 |
| 1961-07 | 570.966895 | 637.778829 |
| 1961-08 | 567.379760 | 638.045925 |
| 1961-09 | 488.192511 | 562.513297 |
| 1961-10 | 418.943257 | 496.747188 |
| 1961-11 | 358.443627 | 439.581313 |
| 1961-12 | 406.662797 | 491.002565 |
predict_interval、predict_quantiles、predict_var、predict_proba 的输出 通常 但 不一定 彼此一致!
一致性是接口的一个弱要求,但并不严格强制执行。
使用概率预测与更新/预测流工作流程#
示例:* 每月观察数据 * 为未来一整年做出概率性预测 * 每月更新预测 * 始于1950年12月
[14]:
# 1949 and 1950
y_start = y[:24]
# Jan 1951 etc
y_update_batch_1 = y.loc[["1951-01"]]
y_update_batch_2 = y.loc[["1951-02"]]
y_update_batch_3 = y.loc[["1951-03"]]
[15]:
# now = Dec 1950
# 1a. fit to data available in Dec 1950
# fh = [1, 2, ..., 12] for all 12 months ahead
forecaster.fit(y_start, fh=1 + np.arange(12))
# 1b. predict 1951, in Dec 1950
forecaster.predict_interval()
# or other proba predict functions
[15]:
| Number of airline passengers | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1951-01 | 125.708002 | 141.744261 |
| 1951-02 | 135.554588 | 154.422393 |
| 1951-03 | 149.921349 | 171.248013 |
| 1951-04 | 140.807416 | 164.337377 |
| 1951-05 | 127.941095 | 153.485009 |
| 1951-06 | 152.968275 | 180.378566 |
| 1951-07 | 167.193932 | 196.351377 |
| 1951-08 | 166.316508 | 197.122174 |
| 1951-09 | 150.425511 | 182.795583 |
| 1951-10 | 128.623026 | 162.485306 |
| 1951-11 | 109.567274 | 144.858726 |
| 1951-12 | 125.641283 | 162.306240 |
[16]:
# time passes, now = Jan 1951
# 2a. update forecaster with new data
forecaster.update(y_update_batch_1)
# 2b. make new prediction - year ahead = Feb 1951 to Jan 1952
forecaster.predict_interval()
# forecaster remembers relative forecasting horizon
[16]:
| Number of airline passengers | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1951-02 | 136.659402 | 152.695661 |
| 1951-03 | 150.894543 | 169.762349 |
| 1951-04 | 141.748827 | 163.075491 |
| 1951-05 | 128.876520 | 152.406481 |
| 1951-06 | 153.906405 | 179.450320 |
| 1951-07 | 168.170068 | 195.580359 |
| 1951-08 | 167.339646 | 196.497090 |
| 1951-09 | 151.478084 | 182.283750 |
| 1951-10 | 129.681609 | 162.051681 |
| 1951-11 | 110.621193 | 144.483474 |
| 1951-12 | 126.786543 | 162.077995 |
| 1952-01 | 121.345111 | 158.010067 |
使用进一步的数据批次重复相同的命令:
[17]:
# time passes, now = Feb 1951
# 3a. update forecaster with new data
forecaster.update(y_update_batch_2)
# 3b. make new prediction - year ahead = Feb 1951 to Jan 1952
forecaster.predict_interval()
[17]:
| Number of airline passengers | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1951-03 | 151.754371 | 167.790630 |
| 1951-04 | 142.481690 | 161.349495 |
| 1951-05 | 129.549186 | 150.875849 |
| 1951-06 | 154.439360 | 177.969321 |
| 1951-07 | 168.623239 | 194.167153 |
| 1951-08 | 167.770038 | 195.180329 |
| 1951-09 | 151.929278 | 181.086722 |
| 1951-10 | 130.167028 | 160.972694 |
| 1951-11 | 111.133094 | 143.503166 |
| 1951-12 | 127.264383 | 161.126664 |
| 1952-01 | 121.830219 | 157.121670 |
| 1952-02 | 132.976427 | 169.641384 |
[18]:
# time passes, now = Feb 1951
# 4a. update forecaster with new data
forecaster.update(y_update_batch_3)
# 4b. make new prediction - year ahead = Feb 1951 to Jan 1952
forecaster.predict_interval()
[18]:
| Number of airline passengers | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1951-04 | 143.421746 | 159.458004 |
| 1951-05 | 130.401490 | 149.269296 |
| 1951-06 | 155.166804 | 176.493468 |
| 1951-07 | 169.300651 | 192.830612 |
| 1951-08 | 168.451755 | 193.995669 |
| 1951-09 | 152.643331 | 180.053622 |
| 1951-10 | 130.913430 | 160.070874 |
| 1951-11 | 111.900912 | 142.706578 |
| 1951-12 | 128.054396 | 160.424468 |
| 1952-01 | 122.645044 | 156.507325 |
| 1952-02 | 133.834100 | 169.125551 |
| 1952-03 | 149.605269 | 186.270225 |
… 等等。
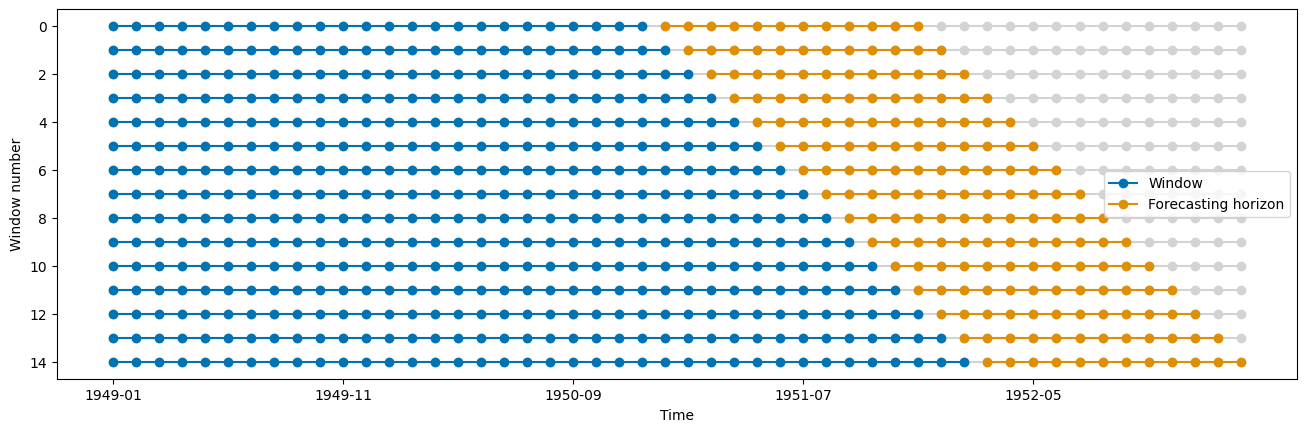
[19]:
from sktime.split import ExpandingWindowSplitter
from sktime.utils.plotting import plot_windows
cv = ExpandingWindowSplitter(step_length=1, fh=fh, initial_window=24)
plot_windows(cv, y.iloc[:50])
[19]:
(<Figure size 1600x480 with 1 Axes>,
<Axes: xlabel='Time', ylabel='Window number'>)
多变量和层次数据的概率预测#
多变量数据:不同变量的第一列索引
[20]:
from sktime.datasets import load_longley
from sktime.forecasting.var import VAR
_, y = load_longley()
mv_forecaster = VAR()
mv_forecaster.fit(y, fh=[1, 2, 3])
# mv_forecaster.predict_var()
[20]:
VAR()Please rerun this cell to show the HTML repr or trust the notebook.
VAR()
层次数据:每个级别的概率预测按行连接,并带有行层次索引
[21]:
from sktime.forecasting.arima import ARIMA
from sktime.utils._testing.hierarchical import _make_hierarchical
y_hier = _make_hierarchical()
y_hier
[21]:
| c0 | |||
|---|---|---|---|
| h0 | h1 | time | |
| h0_0 | h1_0 | 2000-01-01 | 5.272974 |
| 2000-01-02 | 4.416770 | ||
| 2000-01-03 | 2.991815 | ||
| 2000-01-04 | 2.360916 | ||
| 2000-01-05 | 2.269617 | ||
| ... | ... | ... | ... |
| h0_1 | h1_3 | 2000-01-08 | 4.388797 |
| 2000-01-09 | 5.096147 | ||
| 2000-01-10 | 3.347833 | ||
| 2000-01-11 | 3.560713 | ||
| 2000-01-12 | 4.467743 |
96 rows × 1 columns
[22]:
forecaster = ARIMA()
forecaster.fit(y_hier, fh=[1, 2, 3])
forecaster.predict_interval()
[22]:
| 0 | ||||
|---|---|---|---|---|
| 0.9 | ||||
| lower | upper | |||
| h0 | h1 | time | ||
| h0_0 | h1_0 | 2000-01-13 | 1.722621 | 5.035875 |
| 2000-01-14 | 1.880358 | 5.280790 | ||
| 2000-01-15 | 1.924552 | 5.329570 | ||
| h1_1 | 2000-01-13 | 1.847150 | 4.690652 | |
| 2000-01-14 | 1.874098 | 4.740716 | ||
| 2000-01-15 | 1.878830 | 4.745823 | ||
| h1_2 | 2000-01-13 | 2.012331 | 5.262287 | |
| 2000-01-14 | 1.717852 | 4.986732 | ||
| 2000-01-15 | 1.748543 | 5.017644 | ||
| h1_3 | 2000-01-13 | 2.673739 | 4.996850 | |
| 2000-01-14 | 2.589237 | 4.975105 | ||
| 2000-01-15 | 2.599973 | 4.989230 | ||
| h0_1 | h1_0 | 2000-01-13 | 2.596552 | 4.620861 |
| 2000-01-14 | 2.144881 | 4.272040 | ||
| 2000-01-15 | 2.268863 | 4.406453 | ||
| h1_1 | 2000-01-13 | 2.353941 | 5.390139 | |
| 2000-01-14 | 2.267849 | 5.321420 | ||
| 2000-01-15 | 2.259457 | 5.313227 | ||
| h1_2 | 2000-01-13 | 1.877079 | 5.224196 | |
| 2000-01-14 | 1.975364 | 5.387870 | ||
| 2000-01-15 | 2.000103 | 5.415163 | ||
| h1_3 | 2000-01-13 | 2.655375 | 5.049080 | |
| 2000-01-14 | 2.577533 | 4.986714 | ||
| 2000-01-15 | 2.569449 | 4.978829 | ||
(更多关于此内容请参见层次预测笔记本)
概率预测的指标和评估#
概述 - 理论#
预测的 y 与真实的 y 形式不同,因此指标具有形式
metric(y_true: series, y_pred: proba_prediction) -> float
其中 proba_prediction 是特定“概率预测类型”的类型。
即,我们有一个损失/度量 \(L\) 的以下函数签名:
名称 |
参数 |
预测/估计 |
一般形式 |
|---|---|---|---|
点预测 |
条件期望 \(\mathbb{E}[y'\|y]\) |
|
|
方差预测 |
条件方差 \(Var[y'|y]\) |
|
|
分位数预测 |
\(\alpha\in (0,1)\) |
\(\alpha\)-分位数 of \(y'\|y\) |
|
区间预测 |
\(c\in (0,1)\) |
\([a,b]\) 使得 \(P(a\le y' \le b\| y) = c\) |
|
|
\(y'\|y\) 的法则/分布 |
|
指标:通用签名和平均#
介绍使用分位数损失(也称为区间损失或平球损失)的示例,在单变量情况下。
这可以用来评估:
*多个分位数*预测 \(\widehat{\bf y}:=\widehat{y}_1, \dots, \widehat{y}_k\) 对应分位数 \(\bm{\alpha} = \alpha_1,\dots, \alpha_k\) 通过 \(L_{\bm{\alpha}}(\widehat{\bf y}, y) := \frac{1}{k}\sum_{i=1}^k L_{\alpha_i}(\widehat{y}_i, y)\)
区间预测 \([\widehat{a}, \widehat{b}]\) 在对称覆盖率 \(c\) 下通过 \(L_c([\widehat{a},\widehat{b}], y) := \frac{1}{2} L_{\alpha_{low}}(\widehat{a}, y) + \frac{1}{2}L_{\alpha_{high}}(\widehat{b}, y)\) 其中 \(\alpha_{low} = \frac{1-c}{2}, \alpha_{high} = \frac{1+c}{2}\)
(所有这些在其各自的预测对象中都被认为是严格适当的损失)
我们有 三件事可以选择进行平均:
分位数值,如果预测了多个 -
predict_interval(fh, alpha)中alpha的元素预测范围
fh中的时间戳 -fit(fh)或predict_interval(fh, alpha)中的fh元素y中的变量,在多变量情况下(稍后,我们首先看单变量)
我们将首先展示分位数值和时间戳:
仅按
fh时间戳进行平均 ->alpha中每个分位数值一个数字对无内容进行平均 ->
alpha和fh时间戳中每个分位数值的一个数字在
fh和alpha中的分位数值上进行平均 -> 一个数值
pred_quantiles 现在包含分位数预测。alpha 的元素,而 \(t_i\) 是 fh 索引的未来时间戳。[23]:
import numpy as np
from sktime.datasets import load_airline
from sktime.forecasting.theta import ThetaForecaster
y_train = load_airline()[0:24] # train on 24 months, 1949 and 1950
y_test = load_airline()[24:36] # ground truth for 12 months in 1951
# try to forecast 12 months ahead, from y_train
fh = np.arange(1, 13)
forecaster = ThetaForecaster(sp=12)
forecaster.fit(y_train, fh=fh)
pred_quantiles = forecaster.predict_quantiles(alpha=[0.1, 0.25, 0.5, 0.75, 0.9])
pred_quantiles
[23]:
| Number of airline passengers | |||||
|---|---|---|---|---|---|
| 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | |
| 1951-01 | 127.478982 | 130.438212 | 133.726132 | 137.014051 | 139.973281 |
| 1951-02 | 137.638273 | 141.120018 | 144.988491 | 148.856963 | 152.338709 |
| 1951-03 | 152.276580 | 156.212068 | 160.584681 | 164.957294 | 168.892782 |
| 1951-04 | 143.405971 | 147.748041 | 152.572397 | 157.396752 | 161.738823 |
| 1951-05 | 130.762062 | 135.475775 | 140.713052 | 145.950329 | 150.664042 |
| 1951-06 | 155.995358 | 161.053480 | 166.673421 | 172.293362 | 177.351484 |
| 1951-07 | 170.413964 | 175.794494 | 181.772655 | 187.750815 | 193.131346 |
| 1951-08 | 169.718562 | 175.403245 | 181.719341 | 188.035437 | 193.720120 |
| 1951-09 | 154.000332 | 159.973701 | 166.610547 | 173.247393 | 179.220762 |
| 1951-10 | 132.362640 | 138.611371 | 145.554166 | 152.496960 | 158.745692 |
| 1951-11 | 113.464721 | 119.977182 | 127.213000 | 134.448818 | 140.961280 |
| 1951-12 | 129.690414 | 136.456333 | 143.973761 | 151.491189 | 158.257109 |
通过分位点或区间端点计算损失,在
fh时间戳上取平均,即对于fh中的 \(t_i\) 和每个alpha,计算 \(\frac{1}{N} \sum_{i=1}^N L_{\alpha}(\widehat{y}(t_i), y(t_i))\),这是alpha中每个分位数值的一个数字
[24]:
from sktime.performance_metrics.forecasting.probabilistic import PinballLoss
loss = PinballLoss(score_average=False)
loss(y_true=y_test, y_pred=pred_quantiles)
[24]:
0.10 2.706601
0.25 5.494502
0.50 8.162432
0.75 8.003790
0.90 5.220235
Name: 0, dtype: float64
计算每个样本的个体损失值,不进行平均,即,对于
fh中的每个 \(t_i\) 和alpha中的每个 \(\alpha\),计算 \(L_{\alpha}(\widehat{y}(t_i), y(t_i))\),这是每个分位数值 \(\alpha\) 在alpha中和每个时间点 \(t_i\) 在fh中的一个数字。
[25]:
loss.evaluate_by_index(y_true=y_test, y_pred=pred_quantiles)
[25]:
| 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | |
|---|---|---|---|---|---|
| 0 | 1.752102 | 3.640447 | 5.636934 | 5.989462 | 4.524047 |
| 1 | 1.236173 | 2.219995 | 2.505755 | 0.857278 | 0.233871 |
| 2 | 2.572342 | 5.446983 | 8.707660 | 9.782030 | 8.196497 |
| 3 | 1.959403 | 3.812990 | 5.213802 | 4.202436 | 1.135059 |
| 4 | 4.123794 | 9.131056 | 15.643474 | 19.537253 | 19.202362 |
| 5 | 2.200464 | 4.236630 | 5.663290 | 4.279979 | 0.583664 |
| 6 | 2.858604 | 5.801376 | 8.613673 | 8.436889 | 5.281789 |
| 7 | 2.928144 | 5.899189 | 8.640329 | 8.223422 | 4.751892 |
| 8 | 2.999967 | 6.006575 | 8.694726 | 8.064455 | 4.301314 |
| 9 | 2.963736 | 5.847157 | 8.222917 | 7.127280 | 2.928877 |
| 10 | 3.253528 | 6.505704 | 9.393500 | 8.663387 | 4.534848 |
| 11 | 3.630959 | 7.385917 | 11.013119 | 10.881608 | 6.968602 |
计算多分位数预测的损失,平均在
fh时间戳和分位数值alpha上,即,对于 \(t_i\) 在fh中,以及分位数值 \(\alpha_j\),计算 \(\frac{1}{Nk} \sum_{j=1}^k\sum_{i=1}^N L_{\alpha_j}(\widehat{y_j}(t_i), y(t_i))\),这是一个可以用于调优(例如,网格搜索)或整体评估的单一数值
[26]:
from sktime.performance_metrics.forecasting.probabilistic import PinballLoss
loss_multi = PinballLoss(score_average=True)
loss_multi(y_true=y_test, y_pred=pred_quantiles)
[26]:
5.917511873790087
计算多分位数预测的损失,平均分位数值
alpha,对于单个时间戳,即:对于fh中的 \(t_i\) 和分位数值 \(\alpha_j\),计算 \(\frac{1}{k} \sum_{j=1}^k L_{\alpha_j}(\widehat{y_j}(t_i), y(t_i))\),这是一个在fh时刻 \(t_i\) 的单变量时间序列,可用于按时间范围索引进行调整或评估
[27]:
loss_multi.evaluate_by_index(y_true=y_test, y_pred=pred_quantiles)
[27]:
0 4.308598
1 1.410614
2 6.941102
3 3.264738
4 13.527588
5 3.392805
6 6.198466
7 6.088595
8 6.013407
9 5.417993
10 6.470193
11 7.976041
dtype: float64
问题:为什么 score_average 是一个构造函数标志,而 evaluate_by_index 是一个方法?
并非所有损失都是“按索引”计算的,因此
evaluate_by_index逻辑可能会有所不同(例如,伪样本)构造函数参数定义了科学签名的“数学对象”:序列 -> 非时间对象方法定义了操作或“应用方式”,例如,用于调优或报告。
比较 score_average 与 scikit-learn 指标和 sktime 中的 multioutput 参数。
指标:区间 vs 分位数指标#
区间和分位数指标可以互换使用:
覆盖率 处的分位数[28]:
pred_interval = forecaster.predict_interval(coverage=0.8)
pred_interval
[28]:
| Number of airline passengers | ||
|---|---|---|
| 0.8 | ||
| lower | upper | |
| 1951-01 | 127.478982 | 139.973281 |
| 1951-02 | 137.638273 | 152.338709 |
| 1951-03 | 152.276580 | 168.892782 |
| 1951-04 | 143.405971 | 161.738823 |
| 1951-05 | 130.762062 | 150.664042 |
| 1951-06 | 155.995358 | 177.351484 |
| 1951-07 | 170.413964 | 193.131346 |
| 1951-08 | 169.718562 | 193.720120 |
| 1951-09 | 154.000332 | 179.220762 |
| 1951-10 | 132.362640 | 158.745692 |
| 1951-11 | 113.464721 | 140.961280 |
| 1951-12 | 129.690414 | 158.257109 |
损失对象自动识别输入类型并计算相应的区间损失
[29]:
loss(y_true=y_test, y_pred=pred_interval)
[29]:
0.1 2.706601
0.9 5.220235
Name: 0, dtype: float64
[30]:
loss_multi(y_true=y_test, y_pred=pred_interval)
[30]:
3.9634182197580174
通过回测进行评估#
[31]:
from sktime.datasets import load_airline
from sktime.forecasting.model_evaluation import evaluate
from sktime.forecasting.theta import ThetaForecaster
from sktime.performance_metrics.forecasting.probabilistic import PinballLoss
from sktime.split import ExpandingWindowSplitter
# 1. define data
y = load_airline()
# 2. define splitting/backtesting regime
fh = [1, 2, 3]
cv = ExpandingWindowSplitter(step_length=12, fh=fh, initial_window=72)
# 3. define loss to use
loss = PinballLoss()
# default is score_average=True and multi_output="uniform_average", so gives a number
forecaster = ThetaForecaster(sp=12)
results = evaluate(
forecaster=forecaster, y=y, cv=cv, strategy="refit", return_data=True, scoring=loss
)
results.iloc[:, :5].head()
[31]:
| test_PinballLoss | fit_time | pred_quantiles_time | len_train_window | cutoff | |
|---|---|---|---|---|---|
| 0 | 0.865788 | 0.004671 | 0.002910 | 72 | 1954-12 |
| 1 | 0.958340 | 0.003195 | 0.003149 | 84 | 1955-12 |
| 2 | 0.981744 | 0.003315 | 0.002972 | 96 | 1956-12 |
| 3 | 1.411309 | 0.003242 | 0.003038 | 108 | 1957-12 |
| 4 | 1.187198 | 0.003085 | 0.002992 | 120 | 1958-12 |
每一行代表在walkforward设置中的一个训练/测试分割
第一列是测试折叠上的损失
最后两列总结了训练窗口的长度,以及训练/测试之间的截止点
路线图项目:
实现进一步的指标
分布预测指标 - 可能需要 tfp 扩展
高级评估设置
方差损失
欢迎贡献!
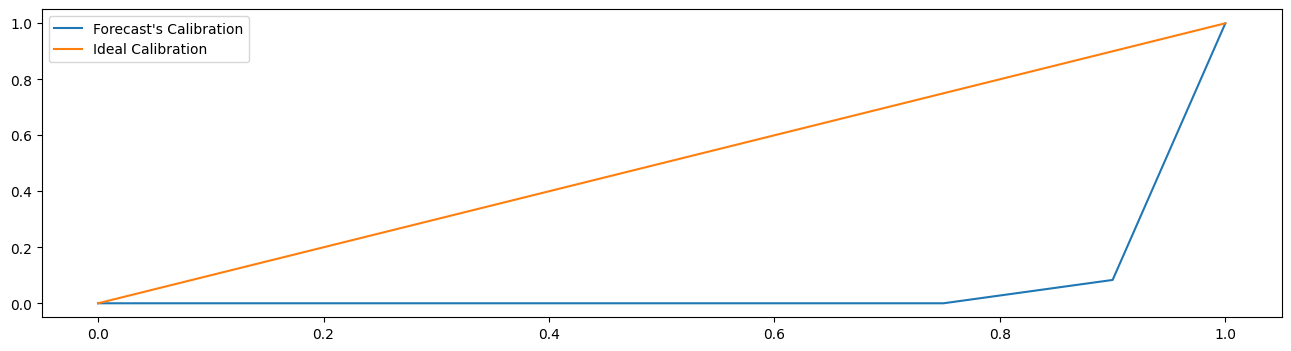
视觉评估#
通常,概率预报的校准是重要的。即,有多少值小于0.1分位数,0.2分位数等。
这种评估可以使用校准图来进行:
[32]:
from sktime.utils.plotting import plot_calibration
plot_calibration(y_true=y_test.loc[pred_quantiles.index], y_pred=pred_quantiles)
[32]:
(<Figure size 1600x400 with 1 Axes>, <Axes: >)
高级组合:管道、调优、简化、将概率预测添加到任何估计器#
composition = 将多个“组件”估计器构建为“复合”估计器
reduction = 使用估计器类型 B 构建估计器类型 A
特殊情况:将概率预测能力添加到非概率预测器
特殊情况:使用概率监督学习者进行概率预测
流水线 = 链接估计器,这里:转换器到一个预测器
tuning = 自动超参数调整,通常通过内部评估循环进行
特殊情况:网格参数搜索和随机参数搜索调优
特殊情况:“Auto-ML”,不仅优化估计器的超参数,还优化估计器的选择
将概率预测添加到非概率预测器#
从一个不产生概率预测的预测器开始:
[33]:
from sktime.forecasting.exp_smoothing import ExponentialSmoothing
my_forecaster = ExponentialSmoothing()
# does the forecaster support probabilistic predictions?
my_forecaster.get_tag("capability:pred_int")
[33]:
False
通过归约包装器可以添加概率预测:
[34]:
# NaiveVariance adds intervals & variance via collecting past residuals
from sktime.forecasting.naive import NaiveVariance
# create a composite forecaster like this:
my_forecaster_with_proba = NaiveVariance(my_forecaster)
# does it support probabilistic predictions now?
my_forecaster_with_proba.get_tag("capability:pred_int")
[34]:
True
复合模型现在可以像任何概率预测器一样使用:
[35]:
y = load_airline()
my_forecaster_with_proba.fit(y, fh=[1, 2, 3])
my_forecaster_with_proba.predict_interval()
[35]:
| Number of airline passengers | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1961-01 | 341.960792 | 522.039207 |
| 1961-02 | 319.835453 | 544.164546 |
| 1961-03 | 307.334056 | 556.665943 |
路线图项目:
更多合成器以启用概率预测
bootstrap 预测区间
简化为概率监督学习
流行的“添加概率能力”包装器
欢迎贡献!
调优与自动机器学习#
ForecastingGridSearchCV 或 ForecastingRandomSearchCV将度量标准更改为调整到概率度量标准
使用相应的概率度量或损失函数
在内部,评估将通过回测评估使用概率度量进行。
evaluate 中使用它或在一个单独的基准测试工作流中使用。[36]:
from sktime.forecasting.model_selection import ForecastingGridSearchCV
from sktime.forecasting.theta import ThetaForecaster
from sktime.performance_metrics.forecasting.probabilistic import PinballLoss
from sktime.split import SlidingWindowSplitter
# forecaster we want to tune
forecaster = ThetaForecaster()
# parameter grid to search over
param_grid = {"sp": [1, 6, 12]}
# evaluation/backtesting regime for *tuning*
fh = [1, 2, 3] # fh for tuning regime, does not need to be same as in fit/predict!
cv = SlidingWindowSplitter(window_length=36, fh=fh)
scoring = PinballLoss()
# construct the composite forecaster with grid search compositor
gscv = ForecastingGridSearchCV(
forecaster, cv=cv, param_grid=param_grid, scoring=scoring, strategy="refit"
)
[37]:
from sktime.datasets import load_airline
y = load_airline()[:60]
gscv.fit(y, fh=fh)
[37]:
ForecastingGridSearchCV(cv=SlidingWindowSplitter(fh=[1, 2, 3],
window_length=36),
forecaster=ThetaForecaster(),
param_grid={'sp': [1, 6, 12]}, scoring=PinballLoss())Please rerun this cell to show the HTML repr or trust the notebook.ForecastingGridSearchCV(cv=SlidingWindowSplitter(fh=[1, 2, 3],
window_length=36),
forecaster=ThetaForecaster(),
param_grid={'sp': [1, 6, 12]}, scoring=PinballLoss())SlidingWindowSplitter(fh=[1, 2, 3], window_length=36)
ThetaForecaster()
PinballLoss()
检查通过调整获得的超参数拟合:
[38]:
gscv.best_params_
[38]:
{'sp': 12}
获取预测:
[39]:
gscv.predict_interval()
[39]:
| Number of airline passengers | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1954-01 | 190.832917 | 217.164705 |
| 1954-02 | 195.638436 | 226.620355 |
| 1954-03 | 221.947952 | 256.967883 |
对于AutoML,使用 MultiplexForecaster 在多个预测器之间进行选择:
[40]:
from sktime.forecasting.compose import MultiplexForecaster
from sktime.forecasting.exp_smoothing import ExponentialSmoothing
from sktime.forecasting.naive import NaiveForecaster, NaiveVariance
forecaster = MultiplexForecaster(
forecasters=[
("naive", NaiveForecaster(strategy="last")),
("ets", ExponentialSmoothing(trend="add", sp=12)),
],
)
forecaster_param_grid = {"selected_forecaster": ["ets", "naive"]}
gscv = ForecastingGridSearchCV(forecaster, cv=cv, param_grid=forecaster_param_grid)
gscv.fit(y)
gscv.best_params_
[40]:
{'selected_forecaster': 'naive'}
带有概率预测器的管道#
sktime 管道与概率预测器兼容:
ForecastingPipeline在将外生X参数传递给预测器之前,会对其应用转换器TransformedTargetForecaster转换y并反向转换预测,包括区间或分位数预测
ForecastingPipeline 接受一系列的转换器和预测器,例如,
[t1, t2, ..., tn, f],
其中 t[i] 是预处理的预测器,而 tp[i] 是后处理的预测器。
fit(y, X, fh) 的作用是:#
X1 = t1.fit_transform(X)X2 = t2.fit_transform(X1)X[n] = t3.fit_transform(X[n-1])f.fit(y=y, x=X[n])
predict_[sth](X, fh) 的作用是:#
X1 = t1.transform(X)X2 = t2.transform(X1)X[n] = t3.transform(X[n-1])f.predict_[sth](X=X[n], fh)
[41]:
from sktime.datasets import load_macroeconomic
from sktime.forecasting.arima import ARIMA
from sktime.forecasting.compose import ForecastingPipeline
from sktime.split import temporal_train_test_split
from sktime.transformations.series.impute import Imputer
[42]:
data = load_macroeconomic()
y = data["unemp"]
X = data.drop(columns=["unemp"])
y_train, y_test, X_train, X_test = temporal_train_test_split(y, X)
[43]:
forecaster = ForecastingPipeline(
steps=[
("imputer", Imputer(method="mean")),
("forecaster", ARIMA(suppress_warnings=True)),
]
)
forecaster.fit(y=y_train, X=X_train, fh=X_test.index[:5])
forecaster.predict_interval(X=X_test[:5])
[43]:
| 0 | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| Period | ||
| 1997Q1 | 5.042704 | 6.119990 |
| 1997Q2 | 3.948564 | 5.235163 |
| 1997Q3 | 3.887471 | 5.253592 |
| 1997Q4 | 4.108211 | 5.506862 |
| 1998Q1 | 4.501319 | 5.913611 |
TransformedTargetForecaster 接受一系列的转换器和预测器,例如,
[t1, t2, ..., tn, f, tp1, tp2, ..., tk],
其中 t[i] 是预处理的预测器,而 tp[i] 是后处理的预测器。
fit(y, X, fh) 的作用是:#
y1 = t1.fit_transform(y)y2 = t2.fit_transform(y1)y3 = t3.fit_transform(y2)y[n] = t3.fit_transform(y[n-1])f.fit(y[n])
yp1 = tp1.fit_transform(yn)yp2 = tp2.fit_transform(yp1)yp3 = tp3.fit_transform(yp2)predict_quantiles(y, X, fh) 的作用是:#
y1 = t1.transform(y)y2 = t2.transform(y1)y[n] = t3.transform(y[n-1])y_pred = f.predict_quantiles(y[n])
y_pred = t[n].inverse_transform(y_pred)y_pred = t[n-1].inverse_transform(y_pred)y_pred = t1.inverse_transform(y_pred)y_pred = tp1.transform(y_pred)y_pred = tp2.transform(y_pred)y_pred = tp[n].transform(y_pred)注意:剩余的概率预测是从 predict_quantiles 推断出来的。
[44]:
from sktime.datasets import load_macroeconomic
from sktime.forecasting.arima import ARIMA
from sktime.forecasting.compose import TransformedTargetForecaster
from sktime.transformations.series.detrend import Deseasonalizer, Detrender
[45]:
data = load_macroeconomic()
y = data[["unemp"]]
[46]:
forecaster = TransformedTargetForecaster(
[
("deseasonalize", Deseasonalizer(sp=12)),
("detrend", Detrender()),
("forecast", ARIMA()),
]
)
forecaster.fit(y, fh=[1, 2, 3])
forecaster.predict_interval()
[46]:
| 0 | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 2009Q4 | 8.949103 | 10.068284 |
| 2010Q1 | 8.639806 | 10.206350 |
| 2010Q2 | 8.438112 | 10.337207 |
[47]:
forecaster.predict_quantiles()
[47]:
| 0 | ||
|---|---|---|
| 0.05 | 0.95 | |
| 2009Q4 | 8.949103 | 10.068284 |
| 2010Q1 | 8.639806 | 10.206350 |
| 2010Q2 | 8.438112 | 10.337207 |
也可以通过 * 双下划线方法快速创建,使用相同的流程:
[48]:
forecaster = Deseasonalizer(sp=12) * Detrender() * ARIMA()
[49]:
forecaster.fit(y, fh=[1, 2, 3])
forecaster.predict_interval()
[49]:
| 0 | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 2009Q4 | 8.949103 | 10.068284 |
| 2010Q1 | 8.639806 | 10.206350 |
| 2010Q2 | 8.438112 | 10.337207 |
构建你自己的概率预测器#
入门:
使用高级 预测扩展模板
扩展模板 = 带有待办块的 Python “填空” 模板,允许您实现自己的、与 sktime 兼容的预测算法。
使用 check_estimator 检查估计器
对于概率预测:
至少实现
predict_quantiles、predict_interval、predict_var、predict_proba中的一个。最佳情况下,实现所有功能,除非与以下默认行为相同
如果只实现了一个,其他的使用以下默认值(按此顺序,依赖可用性):
predict_interval使用predict_quantiles的分位数,反之亦然predict_var使用predict_proba的方差,或使用从predict_quantiles获得的 IQR 的正态分布方差predict_interval或predict_quantiles使用predict_proba分布的分位数predict_proba返回均值为predict和方差为predict_var的正态分布
因此,如果预测残差不正常,可以实现
predict_proba或predict_quantiles。如果需要接口,实现那些最少“转换”必要的部分。
确保将
capability:pred_int标签设置为True
[50]:
# estimator checking on the fly using check_estimator
# suppose NaiveForecaster is your new estimator
from sktime.forecasting.naive import NaiveForecaster
# check the estimator like this
# uncomment this block to run
# from sktime.utils.estimator_checks import check_estimator
#
# check_estimator(NaiveForecaster)
# this prints any failed tests, and returns dictionary with
# keys of test runs and results from the test run
# run individual tests using the tests_to_run arg or the fixtures_to_run_arg
# these need to be identical to test or test/fixture names, see docstring
[51]:
# to raise errors for use in traceback debugging:
# uncomment next line to run
# check_estimator(NaiveForecaster, raise_exceptions=True)
# this does not raise an error since NaiveForecaster is fine, but would if it weren't
摘要#
用于概率预测和概率度量的统一API
集成其他包(例如 scikit-learn、statsmodels、pmdarima、prophet)
复合模型构建的接口相同,是否使用概率(流水线、集成、调优、降维)
toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。
有用的资源#
更多详情,请查看 我们关于使用sktime进行预测的论文 ,我们在其中更详细地讨论了预测API,并使用它来复制和扩展M4研究。
关于预测的良好介绍,请参阅 Hyndman, Rob J., 和 George Athanasopoulos. 预测:原理与实践. OTexts, 2018.
致谢#
笔记本创建: fkiraly
使用 nbsphinx 生成。Jupyter 笔记本可以在这里找到。
