scipy.integrate.

cumulative_simpson#

scipy.integrate.cumulative_simpson(y, *, x=None, dx=1.0, axis=-1, initial=None)[源代码][源代码]#

使用复合辛普森1/3规则累积积分y(x)。在每一点上的样本积分是通过假设每一点与相邻两点之间的二次关系来计算的。

参数:
yarray_like

要积分的值。至少需要沿 axis 提供一个点。如果沿 axis 提供的点少于或等于两个，则无法进行辛普森积分，结果将使用 cumulative_trapezoid 计算。

x类似数组, 可选

要沿其积分的坐标。必须与 y 具有相同的形状，或者必须是与 y 沿 axis 具有相同长度的 1D 数组。x 还必须沿 axis 严格递增。如果 x 为 None（默认），则使用 y 中连续元素之间的间距 dx 进行积分。

dx标量或类数组，可选

y 元素之间的间距。仅在 x 为 None 时使用。可以是浮点数，或与 y 形状相同但沿 axis 长度为 1 的数组。默认值为 1.0。

轴int, 可选

指定要沿其进行积分的轴。默认是 -1（最后一个轴）。

初始标量或类数组，可选

如果给出，则在返回结果的开头插入此值，并将其添加到其余结果中。默认值为 None，这意味着 x[0] 处没有返回值，并且 res 沿积分轴的元素比 y 少一个。可以是浮点数，或与 y 形状相同但沿 axis 长度为一的数组。

返回:
resndarray

沿 axis 对 y 进行累积积分的结果。如果 initial 为 None，则形状使得积分轴的值比 y 少一个。如果给出了 initial，则形状与 y 相同。

参见

numpy.cumsum
cumulative_trapezoid

使用复合梯形法则的累积积分

simpson

使用复合辛普森法则的采样数据积分器

注释

Added in version 1.12.0.

复合辛普森1/3方法可以用来近似计算采样输入函数 \(y(x)\) 的定积分 [1]。该方法假设在任意三个连续采样点所在的区间内，函数关系为二次关系。

考虑三个连续的点：\((x_1, y_1), (x_2, y_2), (x_3, y_3)\)。

假设在三个点之间存在二次关系，子区间在 \(x_1\) 和 \(x_2\) 之间的积分由公式 (8) 给出，参见 [2]。

\[\begin{split}\int_{x_1}^{x_2} y(x) dx\ &= \frac{x_2-x_1}{6}\left[\\ \left\{3-\frac{x_2-x_1}{x_3-x_1}\right\} y_1 + \\ \left\{3 + \frac{(x_2-x_1)^2}{(x_3-x_2)(x_3-x_1)} + \\ \frac{x_2-x_1}{x_3-x_1}\right\} y_2\\\\ - \frac{(x_2-x_1)^2}{(x_3-x_2)(x_3-x_1)} y_3\right]\end{split}\]

在 \(x_2\) 和 \(x_3\) 之间的积分通过交换 \(x_1\) 和 \(x_3\) 的出现来给出。积分对每个子区间分别估计，然后累积求和以获得最终结果。

对于等间距的样本，如果函数是三次或更低次的多项式 [1] 并且子区间的数量是偶数，则结果是精确的。否则，积分对于二次或更低次的多项式是精确的。

参考文献

[2]

Cartwright, Kenneth V. 使用MS Excel和非均匀间隔数据的辛普森规则累积积分。数学科学与数学教育杂志。12 (2): 1-9

示例

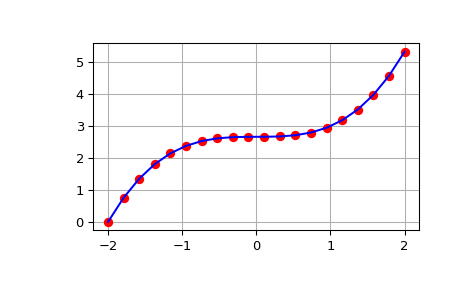
>>> from scipy import integrate
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-2, 2, num=20)
>>> y = x**2
>>> y_int = integrate.cumulative_simpson(y, x=x, initial=0)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, y_int, 'ro', x, x**3/3 - (x[0])**3/3, 'b-')
>>> ax.grid()
>>> plt.show()
../../_images/scipy-integrate-cumulative_simpson-1_00_00.png

cumulative_simpson 的输出类似于通过逐步增加积分上限迭代调用 simpson 的输出，但并不完全相同。

>>> def cumulative_simpson_reference(y, x):
...     return np.asarray([integrate.simpson(y[:i], x=x[:i])
...                        for i in range(2, len(y) + 1)])
>>>
>>> rng = np.random.default_rng()
>>> x, y = rng.random(size=(2, 10))
>>> x.sort()
>>>
>>> res = integrate.cumulative_simpson(y, x=x)
>>> ref = cumulative_simpson_reference(y, x)
>>> equal = np.abs(res - ref) < 1e-15
>>> equal  # not equal when `simpson` has even number of subintervals
array([False,  True, False,  True, False,  True, False,  True,  True])

这是预期的：因为 cumulative_simpson 比 simpson 拥有更多的信息，它通常能对子区间上的基础积分产生更准确的估计。

On this page