solve_ivp#
- scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False, events=None, vectorized=False, args=None, **options)[源代码][源代码]#
求解一个常微分方程组的初值问题。
此函数对给定初始值的常微分方程组进行数值积分:
dy / dt = f(t, y) y(t0) = y0
这里 t 是一个一维自变量(时间),y(t) 是一个 N 维向量值函数(状态),而一个 N 维向量值函数 f(t, y) 决定了微分方程。目标是找到近似满足微分方程的 y(t),给定初始值 y(t0)=y0。
一些求解器支持在复数域中的积分,但请注意,对于刚性ODE求解器,右侧必须是复数可微的(满足柯西-黎曼方程 [11])。要在复数域中解决问题,请传递具有复数数据类型的y0。另一种总是可用的选项是将您的问题分别重写为实部和虚部。
- 参数:
- 有趣可调用
系统右侧:状态
y在时间t的导数。调用签名是fun(t, y),其中t是一个标量,y是一个 ndarray,且len(y) = len(y0)。如果使用args,则需要传递额外的参数(参见args参数的文档)。fun必须返回与y形状相同的数组。更多信息请参见 vectorized。- t_span2-成员序列
积分区间 (t0, tf)。求解器从 t=t0 开始,并积分直到达到 t=tf。t0 和 tf 都必须是浮点数或可通过浮点转换函数解释的值。
- y0类数组, 形状 (n,)
初始状态。对于复杂域中的问题,传递具有复数数据类型(即使初始值是纯实数)的 y0。
- 方法 : 字符串或
OdeSolver,可选字符串或 使用的集成方法:
‘RK45’ (默认): 显式龙格-库塔方法,阶数为5(4) [1]。假设误差控制在第四阶方法的精度内,但步长使用第五阶精确公式(进行局部外推)。使用四次插值多项式进行密集输出 [2]。可以在复数域中应用。
‘RK23’: 显式 Runge-Kutta 方法,阶数为 3(2) [3]。假设精度为二阶方法来控制误差,但使用三阶精确公式进行步进(进行局部外推)。使用三次 Hermite 多项式进行密集输出。可以在复数域中应用。
‘DOP853’: 显式龙格-库塔方法,阶数为8 [13]。Python 实现了最初用 Fortran 编写的“DOP853”算法 [14]。使用了一个精确到7阶的7阶插值多项式进行密集输出。可以在复数域中应用。
‘Radau’: 隐式龙格-库塔方法,属于Radau IIA族,阶数为5 [4]. 误差通过一个三阶精度的嵌入公式来控制。一个满足联结条件的立方多项式用于密集输出。
‘BDF’: 基于导数近似的向后差分公式,采用隐式多步变阶(1到5阶)方法 [5]。实现遵循 [6] 中描述的方法。使用准常步长方案,并通过NDF修改提高精度。可应用于复数域。
‘LSODA’: 具有自动刚度检测和切换功能的 Adams/BDF 方法 [7], [8]。这是 ODEPACK 中 Fortran 求解器的包装器。
显式龙格-库塔方法(’RK23’、’RK45’、’DOP853’)应用于非刚性问题,而隐式方法(’Radau’、’BDF’)应用于刚性问题 [9]。在龙格-库塔方法中,’DOP853’ 推荐用于高精度求解(低值的 rtol 和 atol)。
如果不确定,首先尝试运行 ‘RK45’。如果它进行了异常多的迭代,发散或失败,你的问题很可能是刚性的,你应该使用 ‘Radau’ 或 ‘BDF’。’LSODA’ 也可以是一个不错的选择,但它可能稍微不太方便使用,因为它封装了旧的 Fortran 代码。
你也可以传递一个从
OdeSolver派生的任意类,该类实现了求解器。- t_eval类似数组或无,可选
存储计算解的时间点,必须排序并位于 t_span 内。如果为 None(默认),则使用求解器选择的时间点。
- dense_outputbool, 可选
是否计算连续解。默认是 False。
- 事件可调用对象,或可调用对象列表,可选
要跟踪的事件。如果为 None(默认),则不会跟踪任何事件。每个事件发生在时间与状态的连续函数为零的时刻。每个函数必须具有签名
event(t, y),如果使用args,则必须传递附加参数(参见args参数的文档)。每个函数必须返回一个浮点数。求解器将使用根查找算法找到event(t, y(t)) = 0时 t 的准确值。默认情况下,将找到所有零点。求解器在每个步骤中寻找符号变化,因此如果在一步内发生多次零交叉,可能会错过事件。此外,每个 event 函数可能具有以下属性:- terminal: bool 或 int, 可选
当为布尔值时,是否在事件发生时终止积分。当为整数时,在指定的事件发生次数后终止。如果未赋值,则隐含为 False。
- direction: float, 可选
零交叉的方向。如果 direction 为正,event 仅在从负到正时触发,反之亦然如果 direction 为负。如果为 0,则任一方向都会触发事件。如果未赋值,则隐含为 0。
你可以在 Python 中的任何函数上分配属性,例如
event.terminal = True。- 矢量化bool, 可选
fun 是否可以以矢量化方式调用。默认为 False。
如果
vectorized为 False,fun 将总是以形状为(n,)的y被调用,其中n = len(y0)。如果
vectorized为 True,fun 可能会被调用,参数y的形状为(n, k),其中k是一个整数。在这种情况下,fun 必须表现得使得fun(t, y)[:, i] == fun(t, y[:, i])``(即返回数组的每一列是对应于 ``y的每一列的状态的时间导数)。设置
vectorized=True通过方法 ‘Radau’ 和 ‘BDF’ 可以加快雅可比矩阵的有限差分近似,但在其他方法和某些情况下(例如len(y0)较小时),’Radau’ 和 ‘BDF’ 的执行速度会变慢。- 参数tuple, 可选
传递给用户定义函数的额外参数。如果提供,额外参数将被传递给所有用户定义的函数。因此,例如,如果 fun 的签名是
fun(t, y, a, b, c),那么 jac`(如果提供)和任何事件函数必须具有相同的签名,并且 `args 必须是一个长度为 3 的元组。- **选项
传递给所选求解器的选项。所有已实现的求解器可用的选项如下所列。
- 第一步浮点数或无,可选
初始步长。默认值为 None,这意味着算法应自行选择。
- max_stepfloat, 可选
最大允许步长。默认值为 np.inf,即步长不受限制,完全由求解器决定。
- rtol, atol浮点数或类似数组的对象,可选
相对和绝对容差。求解器保持局部误差估计小于
atol + rtol * abs(y)。这里 rtol 控制相对精度(正确位数),而 atol 控制绝对精度(正确小数位数)。为了达到所需的 rtol,设置 atol 小于rtol * abs(y)的最小值,以便 rtol 主导允许的误差。如果 atol 大于rtol * abs(y),则不能保证正确位数。相反,为了达到所需的 atol,设置 rtol 使得rtol * abs(y)总是小于 atol。如果 y 的分量具有不同的尺度,通过传递形状为 (n,) 的 array_like 给 atol,为不同的分量设置不同的 atol 值可能会有益。默认值为 rtol 为 1e-3,atol 为 1e-6。- jacarray_like, sparse_matrix, callable 或 None, 可选
系统的右侧关于 y 的雅可比矩阵,’Radau’、’BDF’ 和 ‘LSODA’ 方法需要此矩阵。雅可比矩阵的形状为 (n, n),其元素 (i, j) 等于
d f_i / d y_j。定义雅可比矩阵有三种方式:如果数组形式或稀疏矩阵,则假定雅可比矩阵是常数。’LSODA’ 不支持此选项。
如果可调用,则假定雅可比矩阵依赖于 t 和 y;它将在必要时被调用为
jac(t, y)。如果使用了args,则需要传递额外的参数(参见args参数的文档)。对于 ‘Radau’ 和 ‘BDF’ 方法,返回值可能是一个稀疏矩阵。如果为 None(默认),雅可比矩阵将通过有限差分法近似。
通常建议提供雅可比矩阵,而不是依赖于有限差分近似。
- jac_sparsity类似数组、稀疏矩阵或无,可选
定义有限差分近似中雅可比矩阵的稀疏结构。其形状必须是 (n, n)。如果 jac 不是 None,则忽略此参数。如果雅可比矩阵在 每一行 中只有少数非零元素,提供稀疏结构将大大加快计算速度 [R179348322575-10]。零条目表示雅可比矩阵中相应的元素始终为零。如果为 None(默认),则假设雅可比矩阵是稠密的。不支持 ‘LSODA’,请改用 lband 和 uband。
- lband, ubandint 或 None, 可选
定义 ‘LSODA’ 方法的雅可比矩阵带宽的参数,即
jac[i, j] != 0 仅当 i - lband <= j <= i + uband。默认值为 None。设置这些参数需要您的 jac 例程以压缩格式返回雅可比矩阵:返回的数组必须有n列和uband + lband + 1行,其中雅可比矩阵的对角线被写入。具体来说jac_packed[uband + i - j , j] = jac[i, j]。相同的格式用于 scipy.linalg.solve_banded`(检查图示)。这些参数也可以与 ``jac=None` 一起使用,以减少有限差分估计的雅可比矩阵元素的数量。- min_stepfloat, 可选
LSODA方法允许的最小步长。默认情况下,min_step 为零。
- 返回:
- 具有以下字段定义的 Bunch 对象:
- tndarray, 形状 (n_points,)
时间点。
- yndarray, 形状 (n, n_points)
解在 t 时刻的值。
- sol :
OdeSolution或 NoneOdeSolution 或 None 找到的解作为
OdeSolution实例;如果 dense_output 设置为 False,则为 None。- t_eventsndarray 列表或 None
对于每种事件类型,包含一个数组列表,其中检测到该类型的事件。如果 events 为 None,则为 None。
- y_eventsndarray 列表或 None
对于每个 t_events 的值,对应的解的值。如果 events 为 None,则为 None。
- nfev整数
右侧评估的次数。
- njev整数
雅可比矩阵的评估次数。
- nlu整数
LU 分解的次数。
- 状态整数
算法终止的原因:
-1: 集成步骤失败。
求解器成功到达了 tspan 的终点。
1: 发生了终止事件。
- 消息字符串
终止原因的人类可读描述。
- 成功布尔
如果求解器到达区间末端或发生终止事件,则为真(
status >= 0)。
参考文献
[1]J. R. Dormand, P. J. Prince, “A family of embedded Runge-Kutta formulae”, Journal of Computational and Applied Mathematics, Vol. 6, No. 1, pp. 19-26, 1980.
[2]L. W. Shampine, “Some Practical Runge-Kutta Formulas”, Mathematics of Computation,, Vol. 46, No. 173, pp. 135-150, 1986.
[3]P. Bogacki, L.F. Shampine, “A 3(2) Pair of Runge-Kutta Formulas”, Appl. Math. Lett. Vol. 2, No. 4. pp. 321-325, 1989.
[4]E. Hairer, G. Wanner, “Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems”, Sec. IV.8.
[6]L. F. Shampine, M. W. Reichelt, “THE MATLAB ODE SUITE”, SIAM J. SCI. COMPUTE., Vol. 18, No. 1, pp. 1-22, January 1997.
[7]A. C. Hindmarsh, “ODEPACK, A Systematized Collection of ODE Solvers,” IMACS Transactions on Scientific Computation, Vol 1., pp. 55-64, 1983.
[8]L. Petzold, “Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations”, SIAM Journal on Scientific and Statistical Computing, Vol. 4, No. 1, pp. 136-148, 1983.
[10]A. Curtis, M. J. D. Powell, and J. Reid, “On the estimation of sparse Jacobian matrices”, Journal of the Institute of Mathematics and its Applications, 13, pp. 117-120, 1974.
[12]Lotka-Volterra 方程 在维基百科上。
[13]E. Hairer, S. P. Norsett G. Wanner, “Solving Ordinary Differential Equations I: Nonstiff Problems”, Sec. II.
示例
基本指数衰减显示自动选择的时间点。
>>> import numpy as np >>> from scipy.integrate import solve_ivp >>> def exponential_decay(t, y): return -0.5 * y >>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8]) >>> print(sol.t) [ 0. 0.11487653 1.26364188 3.06061781 4.81611105 6.57445806 8.33328988 10. ] >>> print(sol.y) [[2. 1.88836035 1.06327177 0.43319312 0.18017253 0.07483045 0.03107158 0.01350781] [4. 3.7767207 2.12654355 0.86638624 0.36034507 0.14966091 0.06214316 0.02701561] [8. 7.5534414 4.25308709 1.73277247 0.72069014 0.29932181 0.12428631 0.05403123]]
指定需要求解的点。
>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8], ... t_eval=[0, 1, 2, 4, 10]) >>> print(sol.t) [ 0 1 2 4 10] >>> print(sol.y) [[2. 1.21305369 0.73534021 0.27066736 0.01350938] [4. 2.42610739 1.47068043 0.54133472 0.02701876] [8. 4.85221478 2.94136085 1.08266944 0.05403753]]
大炮向上发射,撞击时触发终端事件。事件的
terminal和direction字段通过猴子补丁函数应用。这里y[0]是位置,y[1]是速度。抛射物从位置 0 开始,速度为 +10。注意,积分永远不会达到 t=100,因为事件是终端的。>>> def upward_cannon(t, y): return [y[1], -0.5] >>> def hit_ground(t, y): return y[0] >>> hit_ground.terminal = True >>> hit_ground.direction = -1 >>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10], events=hit_ground) >>> print(sol.t_events) [array([40.])] >>> print(sol.t) [0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02 1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]
使用 dense_output 和 events 来找到位置,即在炮弹轨迹顶点处的位置,该位置为100。顶点不被定义为终点,因此顶点和 hit_ground 都被找到。在 t=20 时没有信息,因此使用 sol 属性来评估解决方案。sol 属性是通过设置
dense_output=True返回的。或者,可以使用 y_events 属性来访问事件发生时的解决方案。>>> def apex(t, y): return y[1] >>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10], ... events=(hit_ground, apex), dense_output=True) >>> print(sol.t_events) [array([40.]), array([20.])] >>> print(sol.t) [0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02 1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01] >>> print(sol.sol(sol.t_events[1][0])) [100. 0.] >>> print(sol.y_events) [array([[-5.68434189e-14, -1.00000000e+01]]), array([[1.00000000e+02, 1.77635684e-15]])]
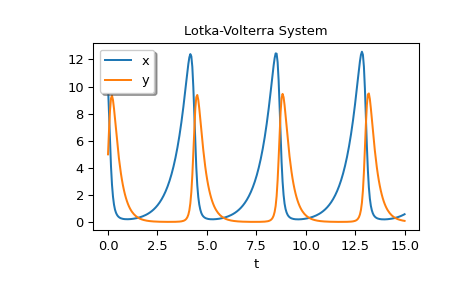
作为一个带有附加参数的系统的例子,我们将实现 Lotka-Volterra 方程 [12]。
>>> def lotkavolterra(t, z, a, b, c, d): ... x, y = z ... return [a*x - b*x*y, -c*y + d*x*y] ...
我们通过 args 参数传入参数值 a=1.5, b=1, c=3 和 d=1。
>>> sol = solve_ivp(lotkavolterra, [0, 15], [10, 5], args=(1.5, 1, 3, 1), ... dense_output=True)
计算一个密集解并绘制它。
>>> t = np.linspace(0, 15, 300) >>> z = sol.sol(t) >>> import matplotlib.pyplot as plt >>> plt.plot(t, z.T) >>> plt.xlabel('t') >>> plt.legend(['x', 'y'], shadow=True) >>> plt.title('Lotka-Volterra System') >>> plt.show()
使用 solve_ivp 求解微分方程
y' = Ay的几个示例,其中矩阵A是复数矩阵。>>> A = np.array([[-0.25 + 0.14j, 0, 0.33 + 0.44j], ... [0.25 + 0.58j, -0.2 + 0.14j, 0], ... [0, 0.2 + 0.4j, -0.1 + 0.97j]])
使用上述的
A和y作为 3x1 向量来求解一个 IVP:>>> def deriv_vec(t, y): ... return A @ y >>> result = solve_ivp(deriv_vec, [0, 25], ... np.array([10 + 0j, 20 + 0j, 30 + 0j]), ... t_eval=np.linspace(0, 25, 101)) >>> print(result.y[:, 0]) [10.+0.j 20.+0.j 30.+0.j] >>> print(result.y[:, -1]) [18.46291039+45.25653651j 10.01569306+36.23293216j -4.98662741+80.07360388j]
使用上述
A解决 IVP,其中y为 3x3 矩阵:>>> def deriv_mat(t, y): ... return (A @ y.reshape(3, 3)).flatten() >>> y0 = np.array([[2 + 0j, 3 + 0j, 4 + 0j], ... [5 + 0j, 6 + 0j, 7 + 0j], ... [9 + 0j, 34 + 0j, 78 + 0j]])
>>> result = solve_ivp(deriv_mat, [0, 25], y0.flatten(), ... t_eval=np.linspace(0, 25, 101)) >>> print(result.y[:, 0].reshape(3, 3)) [[ 2.+0.j 3.+0.j 4.+0.j] [ 5.+0.j 6.+0.j 7.+0.j] [ 9.+0.j 34.+0.j 78.+0.j]] >>> print(result.y[:, -1].reshape(3, 3)) [[ 5.67451179 +12.07938445j 17.2888073 +31.03278837j 37.83405768 +63.25138759j] [ 3.39949503 +11.82123994j 21.32530996 +44.88668871j 53.17531184+103.80400411j] [ -2.26105874 +22.19277664j -15.1255713 +70.19616341j -38.34616845+153.29039931j]]