scipy.spatial.

SphericalVoronoi

class scipy.spatial.SphericalVoronoi(points, radius=1, center=None, threshold=1e-06)

球面上的Voronoi图。

Added in version 0.18.0.

参数:

点浮点数的 ndarray，形状为 (npoints, ndim)

用于构建球面Voronoi图的点的坐标。

半径float, 可选

球的半径 (默认值: 1)

中心浮点数的 ndarray，形状为 (ndim,)

球心 (默认: 原点)

阈值浮动

检测重复点和点与球参数之间不匹配的阈值。（默认值：1e-06）

属性:

点形状为 (npoints, ndim) 的双重数组

在 ndim 维度中的点，用于生成Voronoi图

半径双

球体的半径

中心形状为 (ndim,) 的双重数组

球心

顶点形状为 (nvertices, ndim) 的双重数组

与点对应的Voronoi顶点

区域形状为 (npoints, _ ) 的整数列表列表

第 n 个条目是一个列表，包含属于 points 中第 n 个点的顶点的索引

方法

calculate_areas()

计算Voronoi区域的面积。

Raises:

ValueError

如果 points 中有重复项。如果提供的 radius 与 points 不一致。

参见

Voronoi

N 维中的传统 Voronoi 图。

注释

球面Voronoi图算法的过程如下。首先计算输入点（生成器）的凸包，这等价于球面上的Delaunay三角剖分 [Caroli]。然后使用凸包的邻接信息来围绕每个生成器排序Voronoi区域的顶点。后一种方法相对于基于角度的Voronoi区域顶点排序方法，对浮点数问题敏感度显著降低。

对球面Voronoi算法性能的实证评估表明其具有二次时间复杂度（对数线性是最优的，但算法实现更具挑战性）。

参考文献

[Caroli]

Caroli 等人。 对球体上或接近球体的点的鲁棒且高效的 Delaunay 三角剖分。研究报告 RR-7004，2009。

[VanOosterom]

Van Oosterom 和 Strackee. 平面三角形的立体角。IEEE 生物医学工程学报，2，1983，第 125–126 页。

示例

Try it in your browser!

进行一些导入并在立方体上取一些点：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.spatial import SphericalVoronoi, geometric_slerp
>>> from mpl_toolkits.mplot3d import proj3d
>>> # set input data
>>> points = np.array([[0, 0, 1], [0, 0, -1], [1, 0, 0],
...                    [0, 1, 0], [0, -1, 0], [-1, 0, 0], ])

计算球面Voronoi图：

>>> radius = 1
>>> center = np.array([0, 0, 0])
>>> sv = SphericalVoronoi(points, radius, center)

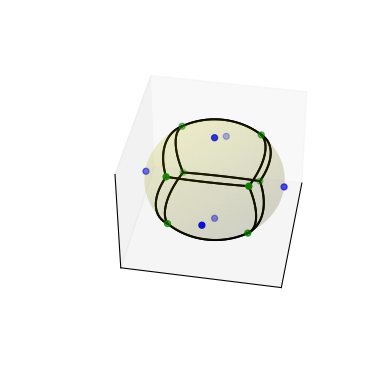
生成图表：

>>> # sort vertices (optional, helpful for plotting)
>>> sv.sort_vertices_of_regions()
>>> t_vals = np.linspace(0, 1, 2000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> # plot the unit sphere for reference (optional)
>>> u = np.linspace(0, 2 * np.pi, 100)
>>> v = np.linspace(0, np.pi, 100)
>>> x = np.outer(np.cos(u), np.sin(v))
>>> y = np.outer(np.sin(u), np.sin(v))
>>> z = np.outer(np.ones(np.size(u)), np.cos(v))
>>> ax.plot_surface(x, y, z, color='y', alpha=0.1)
>>> # plot generator points
>>> ax.scatter(points[:, 0], points[:, 1], points[:, 2], c='b')
>>> # plot Voronoi vertices
>>> ax.scatter(sv.vertices[:, 0], sv.vertices[:, 1], sv.vertices[:, 2],
...                    c='g')
>>> # indicate Voronoi regions (as Euclidean polygons)
>>> for region in sv.regions:
...    n = len(region)
...    for i in range(n):
...        start = sv.vertices[region][i]
...        end = sv.vertices[region][(i + 1) % n]
...        result = geometric_slerp(start, end, t_vals)
...        ax.plot(result[..., 0],
...                result[..., 1],
...                result[..., 2],
...                c='k')
>>> ax.azim = 10
>>> ax.elev = 40
>>> _ = ax.set_xticks([])
>>> _ = ax.set_yticks([])
>>> _ = ax.set_zticks([])
>>> fig.set_size_inches(4, 4)
>>> plt.show()

Go BackOpen In Tab