scipy.special.stdtrit#

scipy.special.stdtrit(df, p, out=None) = <ufunc 'stdtrit'>#

学生 t 分布的第 p 个分位数。

此函数是学生 t 分布累积分布函数 (CDF) 的反函数，返回 t 使得 stdtr(df, t) = p。

返回参数 t，使得 stdtr(df, t) 等于 p。

参数:
dfarray_like

自由度

parray_like

概率

出ndarray，可选

函数结果的可选输出数组

返回:
t标量或ndarray

使得 stdtr(df, t) == p 成立的 t 值

参见

stdtr

学生 t 分布累积分布函数

stdtridf

关于 df 的 stdtr 的逆

scipy.stats.t

学生 t 分布

注释

学生 t 分布也可以通过 scipy.stats.t 获得。直接调用 stdtrit 可以提高性能，相比于 scipy.stats.t 的 ppf 方法（见下面的最后一个例子）。

示例

stdtrit 表示学生 t 分布 CDF 的逆函数，该函数作为 stdtr 提供。在这里，我们计算 df 在 x=1 处的 CDF。然后，stdtrit 在给定相同的 df 值和计算的 CDF 值的情况下，返回 1 直至浮点误差。

>>> import numpy as np
>>> from scipy.special import stdtr, stdtrit
>>> import matplotlib.pyplot as plt
>>> df = 3
>>> x = 1
>>> cdf_value = stdtr(df, x)
>>> stdtrit(df, cdf_value)
0.9999999994418539

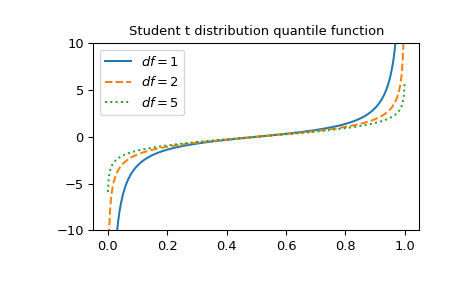
绘制函数以显示三种不同的自由度。

>>> x = np.linspace(0, 1, 1000)
>>> parameters = [(1, "solid"), (2, "dashed"), (5, "dotted")]
>>> fig, ax = plt.subplots()
>>> for (df, linestyle) in parameters:
...     ax.plot(x, stdtrit(df, x), ls=linestyle, label=f"$df={df}$")
>>> ax.legend()
>>> ax.set_ylim(-10, 10)
>>> ax.set_title("Student t distribution quantile function")
>>> plt.show()
../../_images/scipy-special-stdtrit-1_00_00.png

通过为 df 提供一个 NumPy 数组或列表，该函数可以同时计算多个自由度的值：

>>> stdtrit([1, 2, 3], 0.7)
array([0.72654253, 0.6172134 , 0.58438973])

通过为 df 和 p 提供形状兼容广播的数组，可以同时在多个点上计算多个不同自由度的函数。计算 stdtrit 在 4 个点上对于 3 个自由度的结果，得到一个形状为 3x4 的数组。

>>> dfs = np.array([[1], [2], [3]])
>>> p = np.array([0.2, 0.4, 0.7, 0.8])
>>> dfs.shape, p.shape
((3, 1), (4,))

>>> stdtrit(dfs, p)
array([[-1.37638192, -0.3249197 ,  0.72654253,  1.37638192],
       [-1.06066017, -0.28867513,  0.6172134 ,  1.06066017],
       [-0.97847231, -0.27667066,  0.58438973,  0.97847231]])

t 分布也可以通过 scipy.stats.t 获得。直接调用 stdtrit 比调用 scipy.stats.t 的 ppf 方法要快得多。要获得相同的结果，必须使用以下参数化：scipy.stats.t(df).ppf(x) = stdtrit(df, x)。

>>> from scipy.stats import t
>>> df, x = 3, 0.5
>>> stdtrit_result = stdtrit(df, x)  # this can be faster than below
>>> stats_result = t(df).ppf(x)
>>> stats_result == stdtrit_result  # test that results are equal
True
On this page