scipy.stats.

circstd#

scipy.stats.circstd(samples, high=6.283185307179586, low=0, axis=None, nan_policy='propagate', *, normalize=False, keepdims=False)[源代码][源代码]#

计算角度观测样本的圆形标准差。

给定以弧度测量的 \(n\) 个角度观测值 \(x_1, \cdots, x_n\)，它们的 圆标准差 由 ([2], 公式 2.3.11) 定义

\[\sqrt{ -2 \log \left| \frac{1}{n} \sum_{k=1}^n e^{i x_k} \right| }\]

其中 \(i\) 是虚数单位，\(|z|\) 给出复数 \(z\) 的长度。上述表达式中的 \(|z|\) 被称为 平均结果长度。

参数:

示例array_like

输入角度观测数组。一个完整角度的值等于 (high - low)。

高float, 可选

角的主值的上边界。默认值为 2*pi。

低float, 可选

角的主值的下边界。默认值为 0。

规范化布尔值，可选

如果 False``（默认值），返回值根据上述公式计算，输入值按 ``(2*pi)/(high-low) 缩放，输出值按 (high-low)/(2*pi) 缩放（回）。如果 True，输出值不进行缩放，直接返回。

轴int 或 None, 默认: None

如果是一个整数，表示输入数据中要计算统计量的轴。输入数据的每个轴切片（例如行）的统计量将出现在输出的相应元素中。如果为 None，则在计算统计量之前会将输入数据展平。

nan_policy{‘propagate’, ‘omit’, ‘raise’}

定义如何处理输入的 NaN。

propagate: 如果在计算统计量的轴切片（例如行）中存在 NaN，则输出的相应条目将为 NaN。
omit: 在执行计算时，NaN 将被省略。如果在计算统计量的轴切片中剩余的数据不足，则输出的相应条目将为 NaN。
raise: 如果存在 NaN，将引发 ValueError。

keepdimsbool, 默认值: False

如果设置为True，被减少的轴将作为尺寸为1的维度保留在结果中。通过此选项，结果将正确地与输入数组进行广播。

返回:

circstd浮动

循环标准差，可选地归一化。

如果输入数组为空，则返回 np.nan。

参见

circmean: 循环平均值。
circvar: 循环方差。

注释

在小角度极限下，如果 normalize 为 False ，圆标准差接近于 ‘线性’ 标准差。

从 SciPy 1.9 开始，np.matrix 输入（不推荐用于新代码）在计算执行前被转换为 np.ndarray。在这种情况下，输出将是一个标量或适当形状的 np.ndarray，而不是一个 2D 的 np.matrix。同样，虽然掩码数组的掩码元素被忽略，但输出将是一个标量或 np.ndarray，而不是一个 mask=False 的掩码数组。

参考文献

[1]

Mardia, K. V. (1972). 2. 在《方向数据统计》(第18-24页)。学术出版社。DOI:10.1016/C2013-0-07425-7。

[2]

Mardia, K. V. 和 Jupp, P. E. 方向统计。John Wiley & Sons, 1999.

示例

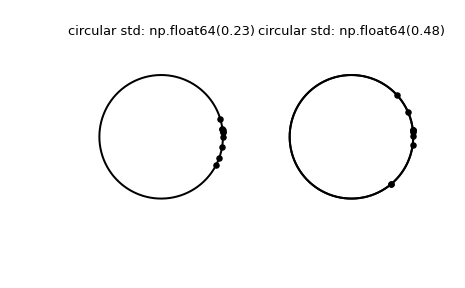
>>> import numpy as np
>>> from scipy.stats import circstd
>>> import matplotlib.pyplot as plt
>>> samples_1 = np.array([0.072, -0.158, 0.077, 0.108, 0.286,
...                       0.133, -0.473, -0.001, -0.348, 0.131])
>>> samples_2 = np.array([0.111, -0.879, 0.078, 0.733, 0.421,
...                       0.104, -0.136, -0.867,  0.012,  0.105])
>>> circstd_1 = circstd(samples_1)
>>> circstd_2 = circstd(samples_2)

绘制样本。

>>> fig, (left, right) = plt.subplots(ncols=2)
>>> for image in (left, right):
...     image.plot(np.cos(np.linspace(0, 2*np.pi, 500)),
...                np.sin(np.linspace(0, 2*np.pi, 500)),
...                c='k')
...     image.axis('equal')
...     image.axis('off')
>>> left.scatter(np.cos(samples_1), np.sin(samples_1), c='k', s=15)
>>> left.set_title(f"circular std: {np.round(circstd_1, 2)!r}")
>>> right.plot(np.cos(np.linspace(0, 2*np.pi, 500)),
...            np.sin(np.linspace(0, 2*np.pi, 500)),
...            c='k')
>>> right.scatter(np.cos(samples_2), np.sin(samples_2), c='k', s=15)
>>> right.set_title(f"circular std: {np.round(circstd_2, 2)!r}")
>>> plt.show()