dunnett#
- scipy.stats.dunnett(*samples, control, alternative='two-sided', random_state=None)[源代码][源代码]#
邓尼特检验:对均值与对照组进行多重比较。
这是对Dunnett原始的单步测试的实现,如[R903271b9c72c-1]_中所述。
- 参数:
- 示例1, 示例2, …1D array_like
每个实验组的样本测量数据。
- 控制1D array_like
对照组的样本测量数据。
- 替代方案{‘双侧’, ‘小于’, ‘大于’}, 可选
定义备择假设。
零假设是样本和对照组背后的分布均值相等。以下是可用的备择假设(默认是’双侧’):
‘双侧’: 样本和对照的基础分布的均值不相等。
less: 样本基础分布的均值小于对照基础分布的均值。
‘greater’: 样本分布的均值大于对照组分布的均值。
- random_state : {None, int,
numpy.random.Generator}, 可选{None, int,} 如果 random_state 是一个整数或 None,则使用
np.random.default_rng(random_state)创建一个新的numpy.random.Generator。如果 random_state 已经是一个Generator实例,则使用提供的实例。随机数生成器用于控制多元 t 分布的随机化准蒙特卡罗积分。
- 返回:
- resDunnett结果
一个包含属性的对象:
- 统计浮点数 ndarray
每次比较的测试计算统计量。索引
i处的元素是组i与对照组之间比较的统计量。- p值浮点数 ndarray
每次比较的测试计算出的 p 值。索引
i处的元素是组i与对照组之间比较的 p 值。
以及以下方法:
- confidence_interval(confidence_level=0.95) :
计算各组与对照组平均值的差异,允许误差范围。
参见
tukey_hsd执行均值的两两比较。
注释
与独立样本 t 检验类似,Dunnett 检验 [1] 用于对样本所来自的分布的均值进行推断。然而,当在固定显著性水平上进行多个 t 检验时,’整体错误率’ - 至少在一个检验中错误地拒绝原假设的概率 - 将超过显著性水平。Dunnett 检验旨在进行多重比较的同时控制整体错误率。
Dunnett’s test 将多个实验组的均值与一个对照组进行比较。Tukey’s Honestly Significant Difference Test 是另一种控制族错误率的多元比较测试,但
tukey_hsd执行 所有 组间成对比较。当不需要实验组间的成对比较时,由于其更高的功效,Dunnett’s test 是更优的选择。这个测试的使用依赖于几个假设。
观察结果在组内和组间都是独立的。
每个组内的观测值呈正态分布。
样本所抽取的分布具有相同的有限方差。
参考文献
[1] (1,2)Charles W. Dunnett. “一种多重比较程序,用于比较多个处理与对照组。”《美国统计协会杂志》,50:272,1096-1121,DOI:10.1080/01621459.1955.10501294,1955年。
示例
在 [1] 中,研究了药物对三组动物血细胞计数测量的影响。
下表总结了两个组接受不同药物的实验结果,以及一个组作为对照组的结果。血细胞计数(每立方毫米百万个细胞)被记录如下:
>>> import numpy as np >>> control = np.array([7.40, 8.50, 7.20, 8.24, 9.84, 8.32]) >>> drug_a = np.array([9.76, 8.80, 7.68, 9.36]) >>> drug_b = np.array([12.80, 9.68, 12.16, 9.20, 10.55])
我们想看看这些组之间的均值是否有显著差异。首先,通过箱线图进行视觉检查。
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1) >>> ax.boxplot([control, drug_a, drug_b]) >>> ax.set_xticklabels(["Control", "Drug A", "Drug B"]) >>> ax.set_ylabel("mean") >>> plt.show()
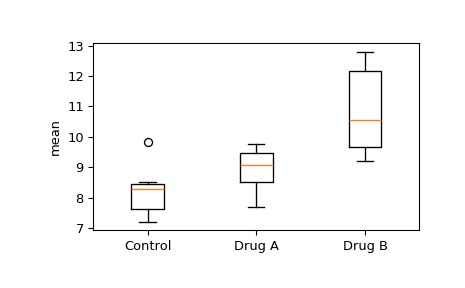
注意药物A组和对照组的四分位距范围重叠,以及药物B组和对照组之间明显的分离。
接下来,我们将使用Dunnett’s检验来评估在控制族错误率(即犯任何错误发现的概率)的情况下,组均值之间的差异是否显著。设零假设为实验组与对照组的均值相同,备择假设为某个实验组的均值与对照组不同。我们认为5%的族错误率是可以接受的,因此我们选择0.05作为显著性的阈值。
>>> from scipy.stats import dunnett >>> res = dunnett(drug_a, drug_b, control=control) >>> res.pvalue array([0.62004941, 0.0059035 ]) # may vary
组A与对照组比较的p值超过0.05,因此我们不拒绝该比较的零假设。然而,组B与对照组比较的p值小于0.05,因此我们认为实验结果是反对零假设而支持备择假设的证据:组B的均值与对照组不同。