scipy.stats.

弗林格

scipy.stats.fligner(*samples, center='median', proportiontocut=0.05, axis=0, nan_policy='propagate', keepdims=False)

执行 Fligner-Killeen 方差相等性检验。

Fligner 检验用于检验所有输入样本来自具有相同方差的总体的零假设。当总体相同时，Fligner-Killeen 检验是无分布的 [2]。

参数:

示例1, 示例2, …array_like

样本数据的数组。长度不必相同。

中心{‘mean’, ‘median’, ‘trimmed’}, 可选

控制用于计算检验统计量的数据函数的键值参数。默认值为 ‘中位数’。

proportiontocutfloat, 可选

当 center 为 ‘trimmed’ 时，这给出了从每一端剪切的数据点的比例。（参见 scipy.stats.trim_mean。）默认值为 0.05。

轴int 或 None, 默认值: 0

如果是一个整数，表示输入数据中要计算统计量的轴。输入数据的每个轴切片（例如行）的统计量将出现在输出的相应元素中。如果为 None，则在计算统计量之前会将输入数据展平。

nan_policy{‘propagate’, ‘omit’, ‘raise’}

定义如何处理输入的 NaN。

• propagate: 如果在计算统计量的轴切片（例如行）中存在 NaN，则输出的相应条目将为 NaN。

• omit: 在执行计算时，NaN 将被省略。如果在计算统计量的轴切片中剩余的数据不足，则输出的相应条目将为 NaN。

• raise: 如果存在 NaN，将引发 ValueError。

keepdimsbool, 默认值: False

如果设置为True，被减少的轴将作为尺寸为1的维度保留在结果中。通过此选项，结果将正确地与输入数组进行广播。

返回:

统计浮动

测试统计量。

p值浮动

假设检验的p值。

参见

bartlett

正态样本中k个方差相等的参数检验

levene

一个稳健的参数检验，用于检验k个方差的相等性

注释

与Levene检验类似，Fligner检验有三种变体，它们在检验中使用的集中趋势度量不同。更多信息请参见 levene。

Conover 等人 (1981) 通过广泛的模拟研究了许多现有的参数和非参数检验，他们得出结论，Fligner 和 Killeen (1976) 以及 Levene (1960) 提出的检验在偏离正态性和功效的稳健性方面似乎更优越 [3]。

从 SciPy 1.9 开始，np.matrix 输入（不推荐用于新代码）在计算执行前被转换为 np.ndarray。在这种情况下，输出将是一个标量或适当形状的 np.ndarray，而不是一个 2D 的 np.matrix。同样，虽然掩码数组的掩码元素被忽略，但输出将是一个标量或 np.ndarray，而不是一个 mask=False 的掩码数组。

参考文献

[1]

Park, C. 和 Lindsay, B. G. (1999). 基于二次推断函数的稳健尺度估计和假设检验。技术报告 #99-03, 似然研究中心, 宾夕法尼亚州立大学。https://cecas.clemson.edu/~cspark/cv/paper/qif/draftqif2.pdf

[2]

Fligner, M.A. 和 Killeen, T.J. (1976)。无分布的两样本尺度检验。《美国统计协会杂志》。71(353), 210-213。

[3]

Park, C. 和 Lindsay, B. G. (1999). 基于二次推断函数的稳健尺度估计和假设检验。技术报告 #99-03, 似然研究中心, 宾夕法尼亚州立大学。

[4]

Conover, W. J., Johnson, M. E. 和 Johnson M. M. (1981). 关于方差同质性检验的比较研究，应用于外大陆架投标数据。技术计量学, 23(4), 351-361.

[5]

C.I. BLISS (1952), 《生物测定的统计学：特别参考维生素》，第499-503页，DOI:10.1016/C2013-0-12584-6。

[6]

B. Phipson and G. K. Smyth. “Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn.” Statistical Applications in Genetics and Molecular Biology 9.1 (2010).

[7]

Ludbrook, J., & Dudley, H. (1998). 为什么置换检验在生物医学研究中优于t检验和F检验。美国统计学家, 52(2), 127-132.

示例

Try it in your browser!

在 [5] 中，研究了维生素C对豚鼠牙齿生长的影响。在一个对照研究中，60个受试者被分为小剂量、中剂量和大剂量组，分别接受每日0.5、1.0和2.0毫克的维生素C剂量。42天后，测量了牙齿的生长情况。

下面的 small_dose、medium_dose 和 large_dose 数组记录了三个组在微米单位的牙齿生长测量值。

>>> import numpy as np
>>> small_dose = np.array([
...     4.2, 11.5, 7.3, 5.8, 6.4, 10, 11.2, 11.2, 5.2, 7,
...     15.2, 21.5, 17.6, 9.7, 14.5, 10, 8.2, 9.4, 16.5, 9.7
... ])
>>> medium_dose = np.array([
...     16.5, 16.5, 15.2, 17.3, 22.5, 17.3, 13.6, 14.5, 18.8, 15.5,
...     19.7, 23.3, 23.6, 26.4, 20, 25.2, 25.8, 21.2, 14.5, 27.3
... ])
>>> large_dose = np.array([
...     23.6, 18.5, 33.9, 25.5, 26.4, 32.5, 26.7, 21.5, 23.3, 29.5,
...     25.5, 26.4, 22.4, 24.5, 24.8, 30.9, 26.4, 27.3, 29.4, 23
... ])

fligner 统计量对样本间方差的差异敏感。

>>> from scipy import stats
>>> res = stats.fligner(small_dose, medium_dose, large_dose)
>>> res.statistic
1.3878943408857916

当方差差异较大时，统计值往往会较高。

我们可以通过将统计量的观测值与零分布进行比较来测试各组间方差的不等性：零分布是指在零假设下，即三组总体方差相等的假设下，统计量值的分布。

在这个测试中，零分布遵循如下所示的卡方分布。

>>> import matplotlib.pyplot as plt
>>> k = 3  # number of samples
>>> dist = stats.chi2(df=k-1)
>>> val = np.linspace(0, 8, 100)
>>> pdf = dist.pdf(val)
>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> def plot(ax):  # we'll reuse this
...     ax.plot(val, pdf, color='C0')
...     ax.set_title("Fligner Test Null Distribution")
...     ax.set_xlabel("statistic")
...     ax.set_ylabel("probability density")
...     ax.set_xlim(0, 8)
...     ax.set_ylim(0, 0.5)
>>> plot(ax)
>>> plt.show()

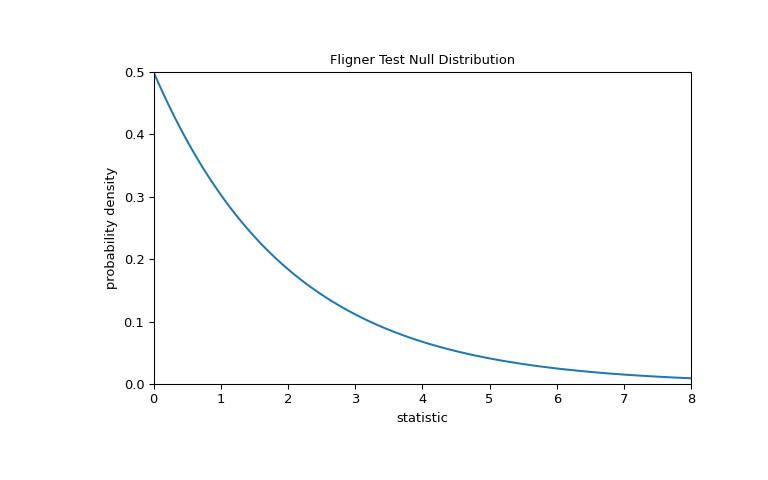
比较通过 p 值量化：零分布中大于或等于统计量观测值的值的比例。

>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> plot(ax)
>>> pvalue = dist.sf(res.statistic)
>>> annotation = (f'p-value={pvalue:.4f}\n(shaded area)')
>>> props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
>>> _ = ax.annotate(annotation, (1.5, 0.22), (2.25, 0.3), arrowprops=props)
>>> i = val >= res.statistic
>>> ax.fill_between(val[i], y1=0, y2=pdf[i], color='C0')
>>> plt.show()

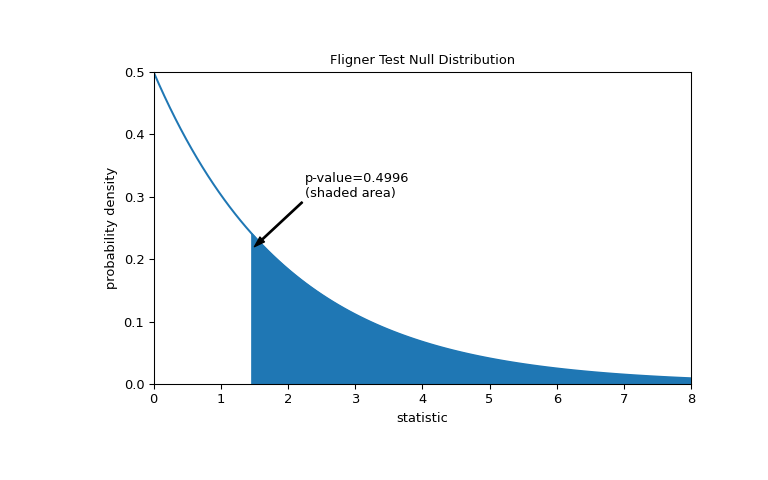
>>> res.pvalue
0.49960016501182125

如果 p 值是“小”的——也就是说，如果从具有相同方差的分布中抽取数据产生如此极端的统计值的概率很低——这可能被视为反对零假设而支持备择假设的证据：各组的方差不相等。注意：

• 反之则不然；也就是说，测试并不用于为零假设提供证据。

• 被认为是“小”的值的阈值是一个选择，应在分析数据之前根据假阳性（错误地拒绝零假设）和假阴性（未能拒绝错误的零假设）的风险来做出 [6]。

• 小的p值并不是*大*效应的证据；相反，它们只能提供“显著”效应的证据，这意味着它们在零假设下不太可能发生。

注意，卡方分布提供了零分布的渐近近似。对于小样本，进行置换检验可能更为合适：在零假设下，所有三个样本都来自同一总体，每个测量值在三个样本中的任何一个中被观察到的可能性是相等的。因此，我们可以通过在许多随机生成的将观察值分配到三个样本的分区下计算统计量，来形成一个随机的零分布。

>>> def statistic(*samples):
...     return stats.fligner(*samples).statistic
>>> ref = stats.permutation_test(
...     (small_dose, medium_dose, large_dose), statistic,
...     permutation_type='independent', alternative='greater'
... )
>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> plot(ax)
>>> bins = np.linspace(0, 8, 25)
>>> ax.hist(
...     ref.null_distribution, bins=bins, density=True, facecolor="C1"
... )
>>> ax.legend(['aymptotic approximation\n(many observations)',
...            'randomized null distribution'])
>>> plot(ax)
>>> plt.show()

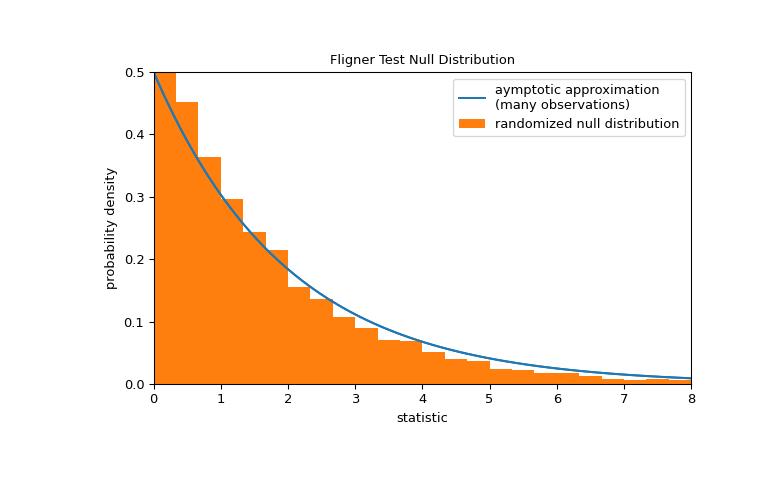
>>> ref.pvalue  # randomized test p-value
0.4332  # may vary

注意，这里计算的p值与上面`fligner`返回的渐近近似值之间存在显著分歧。从排列检验中可以严格得出的统计推断是有限的；尽管如此，它们在许多情况下可能是首选的方法 [7]。

以下是另一个拒绝零假设的通用示例。

测试列表 a、b 和 c 是否来自具有相等方差的总体。

>>> a = [8.88, 9.12, 9.04, 8.98, 9.00, 9.08, 9.01, 8.85, 9.06, 8.99]
>>> b = [8.88, 8.95, 9.29, 9.44, 9.15, 9.58, 8.36, 9.18, 8.67, 9.05]
>>> c = [8.95, 9.12, 8.95, 8.85, 9.03, 8.84, 9.07, 8.98, 8.86, 8.98]
>>> stat, p = stats.fligner(a, b, c)
>>> p
0.00450826080004775

较小的p值表明总体方差不相等。

考虑到 b 的样本方差远大于 a 和 c 的样本方差，这一点并不令人惊讶：

>>> [np.var(x, ddof=1) for x in [a, b, c]]
[0.007054444444444413, 0.13073888888888888, 0.008890000000000002]

Go BackOpen In Tab