scipy.stats.sampling.

TransformedDensityRejection#

class scipy.stats.sampling.TransformedDensityRejection(dist, *, mode=None, center=None, domain=None, c=-0.5, construction_points=30, use_dars=True, max_squeeze_hat_ratio=0.99, random_state=None)#

变换密度拒绝 (TDR) 方法。

TDR 是一种接受/拒绝方法，它利用变换密度的凹性来构造帽函数并自动挤压。与专门针对该分布的算法相比，大多数通用算法非常慢。快速算法设置缓慢且需要大型表格。这种通用方法的目的是提供一种不太慢且只需要短暂设置的算法。该方法可应用于具有 T-凹密度函数的单峰连续分布。更多详情请参见 [1] 和 [2]。

参数:
dist对象

一个具有 pdf 和 dpdf 方法的类实例。

  • pdf: 分布的PDF。PDF的签名应为：def pdf(self, x: float) -> float。即，PDF应接受一个Python浮点数并返回一个Python浮点数。它不需要积分到1，即PDF不需要归一化。

  • dpdf: PDF 对 x（即变量）的导数。必须与 PDF 具有相同的签名。

模式float, 可选

(精确) 分布的模式。默认是 None。

中心float, 可选

分布的模式或均值的近似位置。此位置提供了关于PDF主要部分的一些信息，并用于避免数值问题。默认值为 None。

领域长度为2的列表或元组，可选

对分布的支持。默认是 None。当 None 时：

  • 如果分布对象 dist 提供了 support 方法，它将用于设置分布的域。

  • 否则，支持集被假定为 \((-\infty, \infty)\)。

c{-0.5, 0.}, 可选

为变换函数 T 设置参数 c。默认值为 -0.5。为了构造帽函数，PDF 的变换必须是凹的。这样的 PDF 称为 T-凹。目前支持以下变换：

\[\begin{split}c = 0.: T(x) &= \log(x)\\ c = -0.5: T(x) &= \frac{1}{\sqrt{x}} \text{ (默认)}\end{split}\]
建设点int 或 array_like, 可选

如果是一个整数，它定义了构造点的数量。如果是一个类数组对象，数组的元素将被用作构造点。默认值是30。

use_darsbool, 可选

如果为真，则在设置中使用“去随机化自适应拒绝采样”（DARS）。有关DARS算法的详细信息，请参见[Rf073a3c0c3c3-1]_。默认为True。

max_squeeze_hat_ratiofloat, 可选

设置比率的上限（挤压下方的面积）/（帽子下方的面积）。它必须是一个介于0和1之间的数字。默认值为0.99。

random_state{None, int,}

用于生成均匀随机数流的底层 NumPy 随机数生成器的 NumPy 随机数生成器或种子。如果 random_state 是 None（或 np.random），则使用 numpy.random.RandomState 单例。如果 random_state 是整数，则使用一个新的 RandomState 实例，并以 random_state 为种子。如果 random_state 已经是 Generator 或 RandomState 实例，则使用该实例。

属性:
hat_area

获取发电机帽下方的区域。

squeeze_area

获取生成器挤压下方的区域。

squeeze_hat_ratio

获取生成器的当前比率（挤压下方的面积）/（帽子下方的面积）。

方法

ppf_hat(u)

在 u 处评估帽分布的CDF的逆。

rvs([size, random_state])

来自发行版的示例。

set_random_state([random_state])

设置底层均匀随机数生成器。

参考文献

[1]

UNU.RAN 参考手册，第5.3.16节，“TDR - 变换密度拒绝”，http://statmath.wu.ac.at/software/unuran/doc/unuran.html#TDR

[2]

Hörmann, Wolfgang. “用于从T-凹分布中采样的拒绝技术。” ACM 数学软件汇刊 (TOMS) 21.2 (1995): 182-193

[3]

W.R. Gilks 和 P. Wild (1992)。用于 Gibbs 采样的自适应拒绝采样，应用统计学 41, pp. 337-348。

示例

>>> from scipy.stats.sampling import TransformedDensityRejection
>>> import numpy as np

假设我们有一个密度：

\[\begin{split}f(x) = \begin{cases} 1 - x^2, & -1 \leq x \leq 1 \\ 0, & \text{否则} \end{cases}\end{split}\]

这个密度函数的导数是：

\[\begin{split}\frac{df(x)}{dx} = \begin{cases} -2x, & -1 \leq x \leq 1 \\ 0, & \text{否则} \end{cases}\end{split}\]

注意，PDF 没有积分到 1。由于这是一个基于拒绝的方法，我们不需要一个标准化的 PDF。要初始化生成器，我们可以使用：

>>> urng = np.random.default_rng()
>>> class MyDist:
...     def pdf(self, x):
...         return 1-x*x
...     def dpdf(self, x):
...         return -2*x
...
>>> dist = MyDist()
>>> rng = TransformedDensityRejection(dist, domain=(-1, 1),
...                                   random_state=urng)

域可以非常有用，以截断分布，但要避免每次都将其传递给构造函数，可以通过在分布对象（dist）中提供一个 support 方法来设置默认域：

>>> class MyDist:
...     def pdf(self, x):
...         return 1-x*x
...     def dpdf(self, x):
...         return -2*x
...     def support(self):
...         return (-1, 1)
...
>>> dist = MyDist()
>>> rng = TransformedDensityRejection(dist, random_state=urng)

现在，我们可以使用 rvs 方法从分布中生成样本：

>>> rvs = rng.rvs(1000)

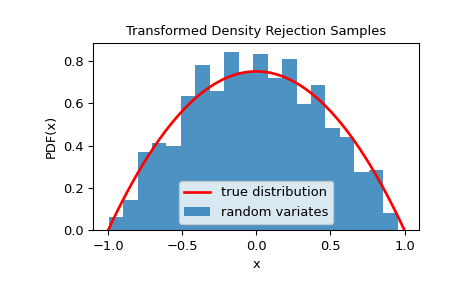
我们可以通过可视化其直方图来检查样本是否来自给定的分布：

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-1, 1, 1000)
>>> fx = 3/4 * dist.pdf(x)  # 3/4 is the normalizing constant
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Transformed Density Rejection Samples')
>>> plt.legend()
>>> plt.show()
../../_images/scipy-stats-sampling-TransformedDensityRejection-1.png
On this page