scipy.stats.

shapiro#

scipy.stats.shapiro(x, *, axis=None, nan_policy='propagate', keepdims=False)[源代码][源代码]#

执行 Shapiro-Wilk 正态性检验。

Shapiro-Wilk 检验用于检验数据是否来自正态分布的零假设。

参数:
xarray_like

样本数据数组。必须包含至少三个观测值。

轴int 或 None, 默认: None

如果是一个整数，表示输入数据中要计算统计量的轴。输入数据的每个轴切片（例如行）的统计量将出现在输出的相应元素中。如果为 None，则在计算统计量之前会将输入数据展平。

nan_policy{‘propagate’, ‘omit’, ‘raise’}

定义如何处理输入的 NaN。

  • propagate: 如果在计算统计量的轴切片（例如行）中存在 NaN，则输出的相应条目将为 NaN。

  • omit: 在执行计算时，NaN 将被省略。如果在计算统计量的轴切片中剩余的数据不足，则输出的相应条目将为 NaN。

  • raise: 如果存在 NaN，将引发 ValueError。

keepdimsbool, 默认值: False

如果设置为True，被减少的轴将作为尺寸为1的维度保留在结果中。通过此选项，结果将正确地与输入数组进行广播。

返回:
统计浮动

测试统计量。

p值浮动

假设检验的p值。

参见

anderson

安德森-达林正态性检验

kstest

Kolmogorov-Smirnov 拟合优度检验。

注释

所使用的算法在 [4] 中描述，但如所述的审查参数并未实现。对于 N > 5000，W 检验统计量是准确的，但 p 值可能不准确。

从 SciPy 1.9 开始，np.matrix 输入（不推荐用于新代码）在计算执行前被转换为 np.ndarray。在这种情况下，输出将是一个标量或适当形状的 np.ndarray，而不是一个 2D 的 np.matrix。同样，虽然掩码数组的掩码元素被忽略，但输出将是一个标量或 np.ndarray，而不是一个 mask=False 的掩码数组。

参考文献

[2] (1,2)

Shapiro, S. S. & Wilk, M.B, “方差分析测试正态性（完整样本）”, Biometrika, 1965, Vol. 52, pp. 591-611, DOI:10.2307/2333709

[3]

Razali, N. M. & Wah, Y. B., “Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors 和 Anderson-Darling 检验的功率比较”, 《统计建模与分析杂志》, 2011年, 第2卷, 第21-33页。

[4]

Royston P., “Remark AS R94: A Remark on Algorithm AS 181: The W-test for Normality”, 1995, Applied Statistics, Vol. 44, DOI:10.2307/2986146

[5]

Phipson B., 和 Smyth, G. K., “排列P值永远不应为零：在随机抽取排列时计算精确P值”, 《遗传学和分子生物学中的统计应用》, 2010年, 第9卷, DOI:10.2202/1544-6115.1585

[6]

Panagiotakos, D. B., “p值在生物医学研究中的价值”, The Open Cardiovascular Medicine Journal, 2008, Vol.2, pp. 97-99, DOI:10.2174/1874192400802010097

示例

假设我们希望从测量数据中推断，医学研究中成年男性体重的分布是否不是正态分布 [2]。体重（磅）记录在下面的数组 x 中。

>>> import numpy as np
>>> x = np.array([148, 154, 158, 160, 161, 162, 166, 170, 182, 195, 236])

对 [1] 和 [2] 的正态性检验首先通过计算一个基于观测值与正态分布预期顺序统计量之间关系的统计量来开始。

>>> from scipy import stats
>>> res = stats.shapiro(x)
>>> res.statistic
0.7888147830963135

这个统计量的值对于从正态分布中抽取的样本往往会很高（接近1）。

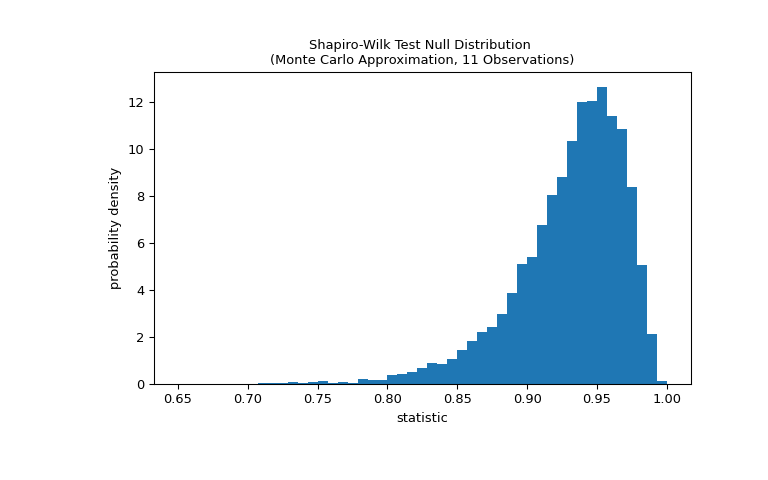
测试是通过将统计量的观测值与零分布进行比较来进行的：零分布是在权重是从正态分布中抽取的零假设下形成的统计量值的分布。对于这种正态性测试，零分布不容易精确计算，因此通常通过蒙特卡罗方法进行近似，即从与 x 相同大小的正态分布中抽取许多样本，并计算每个样本的统计量值。

>>> def statistic(x):
...     # Get only the `shapiro` statistic; ignore its p-value
...     return stats.shapiro(x).statistic
>>> ref = stats.monte_carlo_test(x, stats.norm.rvs, statistic,
...                              alternative='less')
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> bins = np.linspace(0.65, 1, 50)
>>> def plot(ax):  # we'll reuse this
...     ax.hist(ref.null_distribution, density=True, bins=bins)
...     ax.set_title("Shapiro-Wilk Test Null Distribution \n"
...                  "(Monte Carlo Approximation, 11 Observations)")
...     ax.set_xlabel("statistic")
...     ax.set_ylabel("probability density")
>>> plot(ax)
>>> plt.show()
../../_images/scipy-stats-shapiro-1_00_00.png

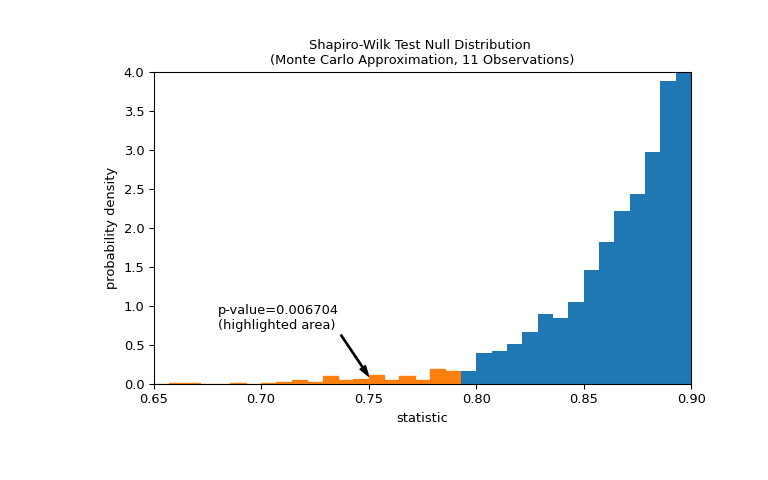
比较通过 p 值量化：零分布中小于或等于统计量观测值的比例。

>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> plot(ax)
>>> annotation = (f'p-value={res.pvalue:.6f}\n(highlighted area)')
>>> props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
>>> _ = ax.annotate(annotation, (0.75, 0.1), (0.68, 0.7), arrowprops=props)
>>> i_extreme = np.where(bins <= res.statistic)[0]
>>> for i in i_extreme:
...     ax.patches[i].set_color('C1')
>>> plt.xlim(0.65, 0.9)
>>> plt.ylim(0, 4)
>>> plt.show
>>> res.pvalue
0.006703833118081093

如果 p 值是“小”的——也就是说，如果从正态分布的总体中抽取数据产生如此极端的统计值的概率很低——这可能被视为反对零假设而支持备择假设的证据：权重并非来自正态分布。请注意：

  • 反之则不然；也就是说，测试不是用来提供证据 支持 零假设的。

  • 被视为“小”的值的阈值是在分析数据之前应做出的选择 [5] ，需考虑到假阳性（错误地拒绝零假设）和假阴性（未能拒绝错误的零假设）的风险。

../../_images/scipy-stats-shapiro-1_01_00.png
On this page